Lajikkeet 

Sinin ja sen graafin ominaisuudet. Sinin, kosinin, tangentin ja kotangentin ominaisuudet


Tässä artikkelissa näytämme kuinka kulman ja luvun sinin, kosinin, tangentin ja kotangentin määritelmät trigonometriassa. Täällä puhumme merkinnöistä, annamme esimerkkejä tietueista, annamme graafisia kuvia. Lopuksi vedämme rinnakkaisuuden sinin, kosinin, tangentin ja kotangentin määritelmien välille trigonometriassa ja geometriassa.

Sivulla navigointi.

Sinin, kosinin, tangentin ja kotangentin määritelmä

Seurataan kuinka käsite sini, kosini, tangentti ja kotangentti muodostuu koulun matematiikan kurssilla. Geometrian tunneilla annetaan suorakulmaisen kolmion terävän kulman sinin, kosinin, tangentin ja kotangentin määritelmä. Ja myöhemmin tutkitaan trigonometriaa, joka viittaa kiertokulman ja luvun siniin, kosiniin, tangenttiin ja kotangenttiin. Annamme kaikki nämä määritelmät, annamme esimerkkejä ja annamme tarvittavat kommentit.

Terävä kulma suorakulmaisessa kolmiossa

Geometrian kurssista tunnetaan suorakulmaisen kolmion terävän kulman sinin, kosinin, tangentin ja kotangentin määritelmät. Ne on annettu suorakulmaisen kolmion sivujen suhteena. Esittelemme niiden muotoilut.

Määritelmä.

Terävän kulman sini suorakulmaisessa kolmiossa on vastakkaisen jalan suhde hypotenuusaan.

Määritelmä.

Suorakulmaisen kolmion terävän kulman kosini on viereisen jalan suhde hypotenuusaan.

Määritelmä.

Suorakulmaisen kolmion terävän kulman tangentti on vastakkaisen jalan suhde viereiseen jalkaan.

Määritelmä.

Suorakulmaisen kolmion terävän kulman kotangentti on viereisen jalan suhde vastakkaiseen jalkaan.

Sinin, kosinin, tangentin ja kotangentin merkintä on myös otettu käyttöön - sin, cos, tg ja ctg, vastaavasti.

Esimerkiksi, jos ABC on suorakulmainen kolmio, jonka suora kulma on C, niin terävän kulman A sini on yhtä suuri kuin vastakkaisen haaran BC suhde hypotenuusaan AB, eli sin∠A=BC/AB.

Näiden määritelmien avulla voit laskea terävän kulman sinin, kosinin, tangentin ja kotangentin arvot suorakulmaisen kolmion sivujen tunnetuista pituuksista sekä sinin, kosinin, tangentti, kotangentti ja yhden sivun pituus, selvitä muiden sivujen pituudet. Jos esimerkiksi tietäisimme, että suorakulmaisessa kolmiossa jalka AC on 3 ja hypotenuusa AB on 7 , voisimme laskea terävän kulman A kosinin määritelmän mukaan: cos∠A=AC/AB=3/7 .

Pyörimiskulma

Trigonometriassa he alkavat tarkastella kulmaa laajemmin - he ottavat käyttöön kiertokulman käsitteen. Kiertokulma, toisin kuin terävä kulma, ei rajoitu kehyksiin 0 - 90 astetta, kiertokulma asteina (ja radiaaneina) voidaan ilmaista millä tahansa reaaliluvulla välillä −∞ - +∞.

Tässä valossa sinin, kosinin, tangentin ja kotangentin määritelmät eivät ole enää terävä kulma, vaan mielivaltaisen suuruinen kulma - kiertokulma. Ne on annettu pisteen A 1 x ja y koordinaattien kautta, johon ns. alkupiste A(1, 0) kulkee kiertyessään kulman α läpi pisteen O ympäri - suorakulmaisen karteesisen koordinaattijärjestelmän alku. ja yksikköympyrän keskipiste.

Määritelmä.

Pyörimiskulman siniα on pisteen A 1 ordinaatta, eli sinα=y .

Määritelmä.

kiertokulman kosiniα:ta kutsutaan pisteen A 1 abskissaksi, eli cosα=x .

Määritelmä.

Pyörimiskulman tangenttiα on pisteen A 1 ordinaatin suhde sen abskissaan, eli tgα=y/x .

Määritelmä.

Pyörimiskulman kotangenttiα on pisteen A 1 abskissan suhde sen ordinaataan, eli ctgα=x/y .

Sini ja kosini määritellään mille tahansa kulmille α, koska voimme aina määrittää pisteen abskissan ja ordinaatin, joka saadaan kiertämällä aloituspistettä kulmalla α. Ja tangenttia ja kotangenttia ei ole määritelty millekään kulmille. Tangenttia ei ole määritelty sellaisille kulmille α, joissa alkupiste menee pisteeseen, jossa on nolla abskissa (0, 1) tai (0, −1) , ja tämä tapahtuu kulmissa 90°+180° k , k∈Z (π /2+π k rad). Todellakin, tällaisissa kiertokulmissa lausekkeessa tgα=y/x ei ole järkeä, koska se sisältää jaon nollalla. Mitä tulee kotangenttiin, sitä ei ole määritelty sellaisille kulmille α, joissa aloituspiste menee pisteeseen, jonka ordinaatit ovat nolla (1, 0) tai (−1, 0) , ja tämä pätee kulmiin 180° k , k ∈Z (π k rad).

Joten sini ja kosini määritellään kaikille kiertokulmille, tangentti on määritelty kaikille kulmille paitsi 90°+180° k , k∈Z (π/2+π k rad) ja kotangentti kaikille kulmille paitsi 180 ° ·k , k∈Z (π·k rad).

Meille jo tutut merkinnät esiintyvät määritelmissä sin, cos, tg ja ctg, niillä merkitään myös kiertokulman sini, kosini, tangentti ja kotangentti (joskus merkintä tan ja cot vastaavat tangenttia ja kotangentti). Joten 30 asteen kiertokulman sini voidaan kirjoittaa sin30°:ksi, tietueet tg(−24°17′) ja ctgα vastaavat kiertokulman tangenttia −24 astetta 17 minuuttia ja kiertokulman α kotangenttia. . Muista, että kun kirjoitetaan kulman radiaanimitta, merkintä "rad" jätetään usein pois. Esimerkiksi kolmen pi rad:n kiertokulman kosini merkitään yleensä cos3 π .

Tämän kappaleen lopuksi on syytä huomata, että puhuttaessa kiertokulman sinistä, kosinista, tangentista ja kotangentista ilmaus "kiertokulma" tai sana "kierto" jätetään usein pois. Eli ilmaisun "kiertokulman sini alfa" sijasta käytetään yleensä ilmaisua "alfan kulman sini" tai vielä lyhyempää - "alfan sini". Sama koskee kosinia, tangenttia ja kotangenttia.

Oletetaan myös, että suorakulmaisen kolmion terävän kulman sinin, kosinin, tangentin ja kotangentin määritelmät ovat yhdenmukaisia ​​0-90 kiertokulman sinin, kosinin, tangentin ja kotangentin määritelmien kanssa. astetta. Perustelemme tämän.

Numerot

Määritelmä.

Luvun sini, kosini, tangentti ja kotangentti t on luku, joka on yhtä suuri kuin kiertokulman sini, kosini, tangentti ja kotangentti t radiaaneina.

Esimerkiksi 8 π:n kosini on määritelmän mukaan luku, joka on yhtä suuri kuin kulman 8 π rad kosini. Ja kulman kosini 8 π rad:ssa on yhtä suuri kuin yksi, joten luvun 8 π kosini on yhtä suuri kuin 1.

On olemassa toinen lähestymistapa luvun sinin, kosinin, tangentin ja kotangentin määrittelyyn. Se koostuu siitä, että jokaiselle reaaliluvulle t on osoitettu yksikköympyrän piste, joka on keskitetty suorakaiteen muotoisen koordinaattijärjestelmän alkupisteeseen, ja sini, kosini, tangentti ja kotangentti määritetään tämän pisteen koordinaattien kautta. Mietitään tätä tarkemmin.

Osoitetaan, kuinka reaalilukujen ja ympyrän pisteiden välinen vastaavuus määritetään:

  • numerolle 0 annetaan aloituspiste A(1, 0) ;
  • positiivinen luku t liittyy yksikköympyrän pisteeseen, johon pääsemme, jos siirrymme ympyrän ympäri aloituspisteestä vastapäivään ja kuljemme t pituisen polun läpi;
  • negatiivinen luku t liittyy yksikköympyrän pisteeseen, johon pääsemme, jos siirrymme ympyrän ympäri aloituspisteestä myötäpäivään ja kuljemme polun, jonka pituus on |t| .

Siirrytään nyt luvun t sinin, kosinin, tangentin ja kotangentin määritelmiin. Oletetaan, että luku t vastaa ympyrän A 1 (x, y) pistettä (esim. luku &pi/2; vastaa pistettä A 1 (0, 1) ).

Määritelmä.

Luvun sini t on lukua t vastaavan yksikköympyrän pisteen ordinaatta, eli sint=y .

Määritelmä.

Luvun kosini t kutsutaan lukua t vastaavan yksikköympyrän pisteen abskissaksi eli kustannus=x .

Määritelmä.

Luvun tangentti t on lukua t vastaavan yksikköympyrän pisteen ordinaatan suhde abskissaan, eli tgt=y/x. Toisessa vastaavassa formulaatiossa luvun t tangentti on tämän luvun sinin ja kosinin suhde, eli tgt=sint/kustannus .

Määritelmä.

Luvun kotangentti t on abskissan suhde lukua t vastaavan yksikköympyrän pisteen ordinaattoihin, eli ctgt=x/y. Toinen muotoilu on seuraava: luvun t tangentti on luvun t kosinin ja luvun t sinin suhde: ctgt=kustannus/sint .

Tässä huomautetaan, että juuri annetut määritelmät sopivat tämän alakohdan alussa annetun määritelmän kanssa. Todellakin, lukua t vastaavan yksikköympyrän piste osuu yhteen pisteen kanssa, joka saadaan kiertämällä aloituspistettä t radiaanin kulman läpi.

Myös tämä seikka kannattaa selventää. Oletetaan, että meillä on sin3-merkintä. Kuinka ymmärtää, onko kyseessä luvun 3 sini vai 3 radiaanin kiertokulman sini? Tämä on yleensä selvää asiayhteydestä, muuten sillä ei todennäköisesti ole väliä.

Kulma- ja numeerisen argumentin trigonometriset funktiot

Edellisessä kappaleessa annettujen määritelmien mukaan jokainen kiertokulma α vastaa hyvin määriteltyä arvoa sin α sekä arvoa cos α . Lisäksi kaikki muut kuin 90°+180° k, k∈Z (π/2+π k rad) kiertokulmat vastaavat arvoja tgα ja muut kuin 180° k, k∈Z (π k rad ) ovat ctgα:n arvot. Siksi sinα, cosα, tgα ja ctgα ovat kulman α funktioita. Toisin sanoen nämä ovat kulma-argumentin funktioita.

Vastaavasti voimme puhua numeerisen argumentin funktioista sini, kosini, tangentti ja kotangentti. Itse asiassa jokainen reaaliluku t vastaa hyvin määriteltyä sintin arvoa sekä kustannusta. Lisäksi kaikki muut luvut kuin π/2+π·k , k∈Z vastaavat arvoja tgt ja luvut π·k , k∈Z vastaavat arvoja ctgt .

Funktioita sini, kosini, tangentti ja kotangentti kutsutaan trigonometriset perusfunktiot.

Kontekstista on yleensä selvää, että kyseessä on kulma- tai numeerisen argumentin trigonometriset funktiot. Muussa tapauksessa voimme pitää riippumatonta muuttujaa sekä kulman mittana (kulma-argumentti) että numeerisena argumenttina.

Koulussa tutkitaan kuitenkin pääasiassa numeerisia funktioita, eli funktioita, joiden argumentit ja vastaavat funktioarvot ovat lukuja. Siksi, jos puhumme funktioista, on suositeltavaa pitää trigonometrisiä funktioita numeeristen argumenttien funktioina.

Geometrian ja trigonometrian määritelmien yhdistäminen

Jos otamme huomioon kiertokulman α välillä 0 - 90 astetta, niin kiertokulman sinin, kosinin, tangentin ja kotangentin määritelmän trigonometrian yhteydessä olevat tiedot ovat täysin yhdenmukaisia ​​sinin, kosinin määritelmien kanssa. , suorakulmaisen kolmion terävän kulman tangentti ja kotangentti, jotka on annettu geometrian kurssilla. Perustellaan tämä.

Piirrä yksikköympyrä suorakulmaiseen karteesiseen koordinaattijärjestelmään Oxy. Huomaa aloituspiste A(1, 0) . Kierretään sitä kulmalla α, joka vaihtelee välillä 0 - 90 astetta, saadaan piste A 1 (x, y) . Pudotetaan kohtisuora A 1 H pisteestä A 1 Ox-akselille.

On helppo nähdä, että suorakulmaisessa kolmiossa kulma A 1 OH on yhtä suuri kuin kiertokulma α, tämän kulman vieressä olevan haaran OH pituus on yhtä suuri kuin pisteen A 1 abskissa, eli |OH |=x, kulman vastakkaisen haaran A 1 H pituus on yhtä suuri kuin pisteen A 1 ordinaatt, eli |A 1 H|=y , ja hypotenuusan OA 1 pituus on yksi , koska se on yksikköympyrän säde. Tällöin, geometrian määritelmän mukaan, terävän kulman α sini suorakulmaisessa kolmiossa A 1 OH on yhtä suuri kuin vastakkaisen haaran suhde hypotenuusaan, eli sinα=|A 1 H|/|OA 1 |= y/1=y . Ja trigonometrian määritelmän mukaan kiertokulman α sini on yhtä suuri kuin pisteen A 1 ordinaatta, eli sinα=y. Tämä osoittaa, että suorakulmaisen kolmion terävän kulman sinin määritelmä vastaa kiertokulman α sinin määritelmää α:lle 0 - 90 astetta.

Vastaavasti voidaan osoittaa, että terävän kulman α kosinin, tangentin ja kotangentin määritelmät ovat yhdenmukaisia ​​kiertokulman α kosinin, tangentin ja kotangentin määritelmien kanssa.

Bibliografia.

  1. Geometria. 7-9 luokkaa: opinnot. yleissivistävää koulutusta varten laitokset / [L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev ja muut]. - 20. painos M.: Koulutus, 2010. - 384 s.: ill. - ISBN 978-5-09-023915-8.
  2. Pogorelov A.V. Geometria: Proc. 7-9 solulle. Yleissivistävä koulutus instituutiot / A. V. Pogorelov. - 2. painos - M.: Enlightenment, 2001. - 224 s.: ill. - ISBN 5-09-010803-X.
  3. Algebra ja alkeisfunktiot: Oppikirja lukion 9. luokan opiskelijoille / E. S. Kochetkov, E. S. Kochetkova; Toimittanut fysiikan ja matemaattisten tieteiden tohtori O. N. Golovin - 4. painos. Moskova: Koulutus, 1969.
  4. Algebra: Proc. 9 solulle. keskim. koulu / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Enlightenment, 1990.- 272 s.: Ill.- ISBN 5-09-002727-7
  5. Algebra ja analyysin alku: Proc. 10-11 solulle. Yleissivistävä koulutus instituutiot / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn ja muut; Ed. A. N. Kolmogorova.- 14. painos- M.: Enlightenment, 2004.- 384 s.: ill.- ISBN 5-09-013651-3.
  6. Mordkovich A.G. Algebra ja analyysin alku. Luokka 10. Klo 14 Osa 1: oppikirja oppilaitoksille (profiilitaso) / A. G. Mordkovich, P. V. Semenov. - 4. painos, lisäys. - M.: Mnemosyne, 2007. - 424 s.: ill. ISBN 978-5-346-00792-0.
  7. Algebra ja matemaattisen analyysin alku. Luokka 10: oppikirja. yleissivistävää koulutusta varten oppilaitokset: perus- ja profiili. tasot /[Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; toim. A. B. Žižtšenko. - 3. painos - I .: Koulutus, 2010. - 368 s.: Ill. - ISBN 978-5-09-022771-1.
  8. Bashmakov M.I. Algebra ja analyysin alku: Proc. 10-11 solulle. keskim. koulu - 3. painos - M.: Enlightenment, 1993. - 351 s.: ill. - ISBN 5-09-004617-4.
  9. Gusev V. A., Mordkovich A. G. Matematiikka (käsikirja teknisiin kouluihin hakijoille): Proc. korvaus.- M.; Korkeampi koulu, 1984.-351 s., ill.

Kaavioista voidaan nähdä, että:

  1. Sini- ja kosinikaaviot vaihtelevat -1:n ja 1:n välillä
  2. Kosinikäyrä on saman muotoinen kuin sinikäyrä, mutta se on siirretty suhteessa siihen 90 o
  3. Sini- ja kosinikäyrät ovat jatkuvia ja toistuvat 360 o jaksolla, tangenttikäyrässä on epäjatkuvuuksia ja toistuu 180 o jaksolla.

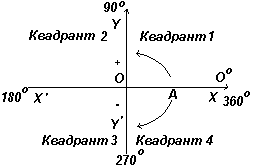Kuvassa vasemmalla on kohtisuorat akselit XX" ja YY"; leikkaava origossa O. Kun työskennellään graafien kanssa, mittaukset oikealle ja ylöspäin O:sta katsotaan positiivisiksi, vasemmalle ja alas O:sta - negatiivisiksi. Anna OA:n pyöriä vapaasti suhteessa O:aan. Kun OA:ta kierretään vastapäivään, mitattu kulma katsotaan positiiviseksi ja myötäpäivään kierrettynä negatiiviseksi.


Ajoittaa. positiivista tai negatiivista
suunta ympyräliikkeessä.

Pyöritään OA vastapäivään siten, että Θ 1 on mikä tahansa kulma ensimmäisessä neljänneksessä, ja rakenna kohtisuora AB saadaksesi suorakulmaisen kolmion OAB kuvassa 2. vasemmalle. Koska kolmion kaikki kolme sivua ovat positiivisia, trigonometriset funktiot sini, kosini ja tangentti ensimmäisessä kvadrantissa ovat positiivisia. (Huomaa, että OA:n pituus on aina positiivinen, koska se on ympyrän säde.)
Pyöritään OA edelleen siten, että Θ 2 on mikä tahansa kulma toisessa neljänneksessä, ja muodosta AC siten, että muodostuu suorakulmainen kolmio OAC. Sitten sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Pyöritään OA edelleen siten, että Θ 3 on mikä tahansa kulma kolmannessa neljänneksessä, ja muodostetaan AD siten, että muodostuu suorakulmainen kolmio OAD. Sitten sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+.


Ajoittaa. Kulmien rakentaminen sisään
erilaisia ​​kvadrantteja.

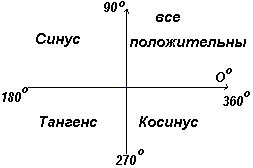Pyöritään OA edelleen siten, että Θ 4 on mikä tahansa kulma neljännessä kvadrantissa, ja konstruoi AE siten, että muodostuu suorakulmainen kolmio OAE. Sitten sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

Ensimmäisessä kvadrantissa kaikilla trigonometrisilla funktioilla on positiiviset arvot, toisessa vain sini on positiivinen, kolmannessa vain tangentti, neljännessä vain kosini, joka näkyy kuvassa 1. vasemmalle.


Mielivaltaisen suuruisten kulmien tuntemus on välttämätöntä, kun löydetään esimerkiksi kaikki kulmat välillä 0 o - 360 o, joiden sini on esimerkiksi 0,3261. Jos syötät laskimeen 0,3261 ja painat sin -1 -painiketta, saamme vastauksen 19,03 o. Välillä 0 o - 360 o on kuitenkin toinen kulma, jota laskin ei näytä. Sini on positiivinen myös toisessa kvadrantissa. Toinen kulma on esitetty kuvassa. alapuolella kulmana Θ, jossa Θ=180 o - 19,03 o = 160,97 o . Siten 19,03 o ja 160,97 o ovat kulmia alueella 0 o - 360 o, joiden sini on 0,3261.

Ole varovainen! Laskin antaa vain yhden näistä arvoista. Toinen arvo tulisi määrittää mielivaltaisen suuruusluokan kulmien teorian mukaan.

Esimerkki 1

Etsi kaikki kulmat välillä 0 o - 360 o, joiden sini on -0,7071

Ratkaisu:
Kulmat, joiden sini on -0,7071 o, ovat kolmannessa ja neljännessä neljänneksessä, koska sini on negatiivinen niissä kvadranteissa (katso kuva vasemmalla).

Ajoittaa. Kaikkien kulmien etsiminen
annettu siniarvo (esimerkki)


Seuraavasta kuvasta Θ = arcsin 0,7071 = 45 o . Kaksi kulmaa välillä 0 o - 360 o, joiden sini on -0,7071, ovat 180 o +45 o \u003d 225 o ja 360 o - 45 o \u003d 315 o.


Merkintä. Laskin antaa vain yhden vastauksen.
Ajoittaa. Kaikkien kulmien etsiminen
annettu siniarvo (esimerkki)

Esimerkki 2

Etsi kaikki kulmat välillä 0 o - 360 o, joiden tangentti on 1,327.

Ratkaisu:
Tangentti on positiivinen ensimmäisessä ja kolmannessa neljänneksessä - kuva 2. vasemmalle.
Ajoittaa. Kaikkien kulmien etsiminen

Alla olevasta kuvasta Θ = arctan1,327= 53 o .
Kaksi kulmaa välillä 0 o - 360 o, joiden tangentti on 1,327, ovat 53 o ja 180 o + 53 o, ts. 233o.
Ajoittaa. Kaikkien kulmien etsiminen
annettu tangentin arvo (esimerkki)

Olkoon OR kuvassa. vasemmalla on yksikköpituinen vektori, joka pyörii vapaasti vastapäivään O:n ympäri. Yksi kierros tuottaa kuvan 1 mukaisen ympyrän. ja jaettuna 15 o:n sektoreilla. Jokaisella säteellä on vaaka- ja pystykomponentti. Esimerkiksi 30 o pystykomponentti on TS ja vaakakomponentti OS.

Trigonometristen funktioiden määritelmästä
sin30 o =TS/TO=TS/1, ts. TS = sin30o ja cos30 o =OS/TO=OS/1, ts. OS=cos30o

Pystykomponentti TS voidaan piirtää muodossa T"S", joka on yhtä suuri kuin arvo, joka vastaa 30° kulmaa y vs x -kulmakuvaajassa. Jos kaikki pystysuorat komponentit, kuten TS, siirretään kuvaajaan, saadaan sinimuoto, joka näkyy kuvassa 1. edellä.


Jos kaikki vaakakomponentit, kuten käyttöjärjestelmä, projisoidaan y:n ja x:n kuvaajalle, saat kosiniaallon. Nämä projektiot on helppo visualisoida piirtämällä uudelleen ympyrä, jonka säde TAI ja kulmat ovat pystysuorassa, kuten vasemmalla olevassa kuvassa näkyy.
Kuvasta vasemmalla näet, että siniaalto on saman muotoinen kuin kosiniaalto, mutta siirtynyt 90 o .




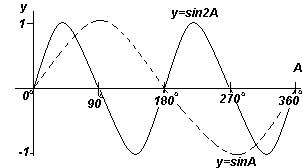Jaksofunktiot ja jakso
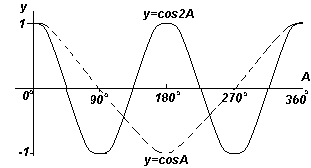
Jokainen neljässä kuviossa esitetyistä funktiokaavioista. edellä, toistetaan kulman A kasvaessa, joten niitä kutsutaan jaksolliset toiminnot.
Funktiot y=sinA ja y=cosA toistetaan joka 360 o (tai 2π radiaani), joten 360 o kutsutaan ajanjaksoa näitä toimintoja. Funktiot y=sin2A ja y=cos2A toistuvat joka 180 o (tai π radiaani), joten 180 o on näiden funktioiden jakso.
Yleensä jos y=sinpA ja y=cospA (missä p on vakio), niin funktion jakso on 360 o /p (tai 2π/p radiaania). Jos y=sin3A, niin tämän funktion jakso on 360 o /3= 120 o , jos y=cos4A, niin tämän funktion jakso on 360 o /4= 90 o .

Amplitudi
Amplitudi kutsutaan sinusoidin maksimiarvoksi. Jokaisen kaavion 1-4 amplitudi on +1 (eli ne vaihtelevat +1:n ja -1:n välillä). Kuitenkin, jos y=4sinA, kukin sinA-arvoista kerrotaan 4:llä, joten suurin amplitudiarvo on 4. Vastaavasti arvolla y=5cos2A amplitudi on 5 ja jakso on 360 o /2= 180 o .

Esimerkki 3
Rakenna y=3sin2A alueella A= 0 o - A=360 o .

Ratkaisu:
Amplitudi = 3, jakso = 360 o /2 = 180 o .

Esimerkki 4
Piirrä y=4cos2x alueella x=0 o - x=360 o

Ratkaisu:
Amplitudi = 4. jakso = 360 o /2 =180 o .


Lag ja lyijykulmat
Sini- ja kosinikäyrät eivät aina ala 0°:sta. Tämän seikan huomioon ottamiseksi jaksollinen funktio esitetään muodossa y=sin(A± α), missä α on vaihesiirto suhteessa y=sinA ja y=cosA.

Kun olet laatinut arvotaulukon, voit piirtää funktion y=sin(A-60 o), joka on esitetty kuvassa. vasemmalle. Jos y=sinA-käyrä alkaa kohdasta 0 o, niin y=sin(A-60 o) -käyrä alkaa kohdasta 60 o (eli sen nolla-arvo on 60 o oikealla). Näin ollen sanotaan, että y=sin(A-60 o) myöhään suhteessa y=sinA:aan 60°.
Ajoittaa. y = sin(A-60 o) (siniaalto).

Kun olet laatinut arvotaulukon, voit piirtää funktion y=cos(A+45 o), joka näkyy kuvassa 1. alla.
Jos käyrä y=cosA alkaa kohdasta 0 o, niin käyrä y=cos(A+45 o) alkaa 45 o vasemmalle (eli sen nolla-arvo on 45 o aikaisemmin).
Siten käyrän sanotaan olevan y=cos(A+45 o) edellä kuvaaja y=cosA 45°:ssa.
Ajoittaa. y = cos(A+45 o) (kosini).

Yleensä kuvaaja y=sin(A-α) on jäljessä suhteessa y=sinA:hen kulman α verran.
Kosiniaalto on saman muotoinen kuin siniaalto, mutta alkaa 90 o vasemmalle, ts. edellä häntä 90 o . Siksi cosA=sin(A+90o).

Esimerkki 5
Piirrä y=5sin(A+30 o) välillä A=0 o - A=360 o


Ratkaisu:
Amplitudi = 5, jakso = 360 o /1 = 360 o .
5sin(A+30 o) johtaa 5sinA:ta 30 o:lla eli. alkaa 30o aikaisemmin.
Kaavio y=5sin(A+30 o) (sinusoidi).

Esimerkki 6
Piirrä y=7sin(2A-π/3) välillä A=0 o - A=360 o .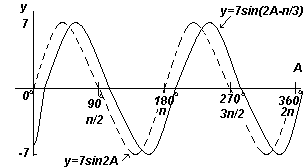

Ratkaisu:
Amplitudi = 7, jakso = 2π/2= π radiaania
Yleisesti y=sin(pt-α) viivästyy suhteessa y=sinpt:hen α/p:llä, siksi 7sin(2A-π/3) on jäljessä suhteessa 7sin2A:een (π/3)/2:lla, ts. per π/6 radiaania tai 30 o

Sinusoidi muotoa Asin(ωt±α). vaihekulma. Vaiheen siirto.

Olkoon OR kuvassa. vasemmalla on vektori, joka pyörii vapaasti vastapäivään O:n ympäri nopeudella ω radiaania/s. Pyörivää vektoria kutsutaan vaihevektori. t sekunnin ajan kuluttua OR pyörii kulman ωt radiaania läpi (vasemmalla olevassa kuvassa tämä on kulma TOR). Jos ST on konstruoitu kohtisuoraan OR:ta vastaan, niin sinωt=ST/OT, ts. ST = OTsinωt.
Jos kaikki tällaiset pystysuuntaiset komponentit projisoidaan y:n ja ωt:n kuvaajalle, saadaan sinimuoto, jonka amplitudi on TAI.

Jos vaihevektori TAI tekee yhden kierroksen (eli 2π radiaania) T sekunnissa, niin kulmanopeus ω=2π/T rad/s, mistä
Т=2π/ ω (s), missä
T on ajanjaksoa
Kutsutaan kokonaisten jaksojen lukumäärää, jotka kuluvat 1 sekunnissa taajuus f.
Taajuus = (jaksojen lukumäärä)/(sekunti) = 1/ T = ω/2π Hz, nuo. f = ω/2π Hz
Siksi kulmanopeus
ω = 2πf rad/s.

Jos yleensä sinifunktio näyttää tältä y=sin(ωt± α), niin
A - amplitudi
ω - kulmanopeus
2π/ω - jakso T, s
ω/2π - taajuus f, Hz
α on johto- tai viivekulma (suhteessa arvoon y=Аsinωt) radiaaneina, sitä kutsutaan myös vaihekulmaksi.

Esimerkki 7
Vaihtovirta annetaan muodossa i=20sin(90πt+0.26) ampeeria. Määritä amplitudi, jakso, taajuus ja vaihekulma (asteina)

Ratkaisu:
i \u003d 20sin (90πt + 0,26) A, joten
amplitudi on 20 A
kulmanopeus ω=90π, joten
kausi T= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
taajuus f\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
vaihekulma α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.

Esimerkki 8
Värähtelymekanismin suurin siirtymä on 3 m ja taajuus 55 Hz. Ajanhetkellä t=0 siirtymä on 100 cm. Ilmaise muutos yleisessä muodossa Аsin(ωt± α).

Ratkaisu
Amplitudi = suurin siirtymä = 3m
Kulmanopeus ω=2πf = 2π(55) = 110 rad/s
Siksi siirtymä on 3sin(110πt + α) m.
Kun t = 0 siirtymä = 100 cm = 1 m.
Siksi 1 = 3sin(0 + α), so. sinα=1/3=0,33
Siksi α=arcsin0,33=19 o
Eli offset on 3sin(110 πt + 0,33).

Esimerkki 9
Vaihtovirtapiirin hetkellisen jännitteen arvo millä tahansa t sekunnissa on annettu muodossa v=350sin(40πt-0.542)V. Löytö:
a) Amplitudi, jakso, taajuus ja vaihekulma (asteina)
b) jännitteen arvo, kun t = 0
c) jännitteen arvo, kun t = 10 ms
d) aika, joka kuluu ennen kuin jännite saavuttaa ensimmäisen kerran 200 V:n.
Ratkaisu:
a) Amplitudi on 350 V, kulmanopeus ω=40π
Siten,
jakso Т=2π/ ω=2π/40π=0,05 s =50 ms
taajuus f=1/T=1/0,05=20 Hz
vaihekulma \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o viiveellä suhteessa v \u003d 350sin (40πt)
b) Jos t \u003d 0, niin v \u003d 350sin (0-0,542) \u003d 350sin (-31 o) \u003d -180,25 V
c) Jos t \u003d 10 ms, niin v \u003d 350sin (40π10 / 10 3 -0,542) \u003d 350sin (0,714) \u003d 350sin41 o \u003d V 22
d) Jos v = 200 JA, niin 200 = 350sin(40πt-0,542) 200/350 = sin(40πt-0,542)

Ajoittaa. Värähtelevä mekanismi
(esimerkki, sinusoidi).

v = 350sin(40πt-0,542) Siksi (40πt-0,542) = arcsin200/350 = 35 o tai 0,611 rad.
40πt = 0,611 + 0,542 = 1,153.
Siksi, jos v = 200 V, niin aika t = 1,153/40π = 9,179 ms

Sinin ja kosinin geometrinen määritelmä

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α on radiaaneina ilmaistu kulma.

Sinus on suorakulmaisen kolmion hypotenuusan ja haaran välisen kulman α trigonometrinen funktio, joka on yhtä suuri kuin vastakkaisen haaran pituuden suhde |BC| hypotenuusan pituuteen |AB|.

Kosini (cos α) on suorakulmaisen kolmion hypotenuusan ja haaran välisen kulman α trigonometrinen funktio, joka on yhtä suuri kuin viereisen haaran pituuden suhde |AC| hypotenuusan pituuteen |AB|.

Trigonometrinen määritelmä

Yllä olevien kaavojen avulla voit löytää terävän kulman sinin ja kosinin. Mutta sinun on opittava laskemaan mielivaltaisen kokoisen kulman sini ja kosini. Suorakulmainen kolmio ei anna tällaista mahdollisuutta (esimerkiksi tylppä kulma ei voi olla siinä); siksi tarvitaan yleisempi sinin ja kosinin määritelmä, joka sisältää nämä kaavat erikoistapauksena.

Trigonometrinen ympyrä tulee apuun. Olkoon jokin kulma annettu; se vastaa trigonometrisen ympyrän samannimistä pistettä.

Riisi. 2. Sinin ja kosinin trigonometrinen määritelmä

Kulman kosini on pisteen abskissa. Kulman sini on pisteen ordinaatta.

Kuvassa Kuvassa 2 kulma on otettu teräväksi, ja on helppo ymmärtää, että tämä määritelmä on yhteneväinen yleisen geometrisen määritelmän kanssa. Todellakin, näemme suorakulmaisen kolmion, jossa on yksikköhypotenuusa O ja terävä kulma. Tämän kolmion viereinen haara on cos (vrt. kuvioon 1) ja samalla pisteen abskissa; vastakkainen jalka on sin (kuten kuvassa 1) ja samalla pisteen ordinaatta.

Mutta nyt ensimmäinen neljännes ei enää rajoita meitä, vaan meillä on mahdollisuus laajentaa tätä määritelmää mihin tahansa kulmaan. Kuvassa Kuva 3 näyttää, mikä on kulman sini ja kosini toisella, kolmannella ja neljännellä neljänneksellä.

Riisi. 3. Sini ja kosini II, III ja IV neljänneksissä

Sinin ja kosinin taulukkoarvot

Nollakulma \(\SUURI 0^(\circ ) \)

Pisteen 0 abskissa on 1, pisteen 0 ordinaatta on 0. Siten,

cos 0 = 1 sin 0 = 0

Kuva 4. Nollakulma

Kulma \(\SUURI \frac(\pi)(6) = 30^(\circ ) \)

Näemme suorakulmaisen kolmion, jossa on yksikköhypotenuusa ja terävä kulma 30°. Kuten tiedät, kulmaa 30 ° vastapäätä oleva jalka on yhtä suuri kuin puolet hypotenuusasta 1; toisin sanoen pystysuora jalka on yhtä suuri kuin 1/2 ja siksi

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Löydämme vaakasuuntaisen haaran Pythagoraan lauseella (tai, mikä on sama, löydämme kosinin trigonometrisen pääidentiteetin mukaan):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 Miksi näin tapahtuu? Leikkaa sen korkeutta pitkin tasasivuinen kolmio, jonka sivu on 2! Se jakautuu kahdeksi suorakulmaiseksi kolmioksi, joissa on hypotenuusa 2, terävä kulma 30° ja pienempi jalka 1.

Kuva 5. Kulma π / 6

Kulma \(\SUURI \frac(\pi)(4) = 45^(\circ ) \)

Tässä tapauksessa suorakulmainen kolmio on tasakylkinen; 45° kulman sini ja kosini ovat keskenään yhtä suuret. Merkitään ne toistaiseksi x:llä. Meillä on:

\[ x^(2) + x^(2) = 1 \]

mistä \(x=\frac(\sqrt(2) )(2) \). Siten,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Kuva 5. Kulma π / 4

Sinin ja kosinin ominaisuudet

Hyväksytyt nimitykset

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Jaksoisuus

Funktiot y = sin x ja y = cos x ovat jaksollisia jaksolla 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Pariteetti

Sinifunktio on outo. Kosinifunktio on parillinen.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Määritelmäalueet ja arvot, ääripäät, lisäys, lasku

Sinin ja kosinin pääominaisuudet on esitetty taulukossa ( n- kokonaisluku).

\(\pieni< x < \) \(\pieni -\pi + 2\pi n \) \(\pieni< x < \) \(\small 2\pi n \)
Laskeva \(\pieni \dfrac(\pi)2 + 2\pi n \)\(\pieni< x < \) \(\pieni \dfrac(3\pi)2 + 2\pi n \) \(\pieni 2\pi n \) \(\pieni< x < \) \(\pi + \small 2\pi n \)
Maksimit, \(\pieni x = \) \(\pieni \dfrac(\pi)2 + 2\pi n \) \(\pieni x = 2\pi n\)
Minimi, \(\pieni x = \) \(\pieni -\dfrac(\pi)2 + 2\pi n \) \(\pieni x = \) \(\pieni \pi + 2\pi n \)
Nollat, \(\pieni x = \pi n \) \(\pieni x = \dfrac(\pi)2 + \pi n \)
Leikkauspisteet y-akselin kanssa, x = 0 y = 0 y = 1

Peruskaavat, jotka sisältävät sinin ja kosinin

Neliöiden summa

\(\sin^2 x + \cos^2 x = 1 \)

Sini- ja kosinisumma- ja erotuskaavat

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Kaavat sinien ja kosinien tulolle

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)

Summa- ja erotuskaavat

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Sinin ilmaisu kosinin kautta

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Kosinin ilmaus sinin kautta

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Ilmaisu tangentin suhteen

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

klo \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

klo \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Taulukko sinistä ja kosineista, tangenteista ja kotangenteista

Tämä taulukko näyttää sinien ja kosinien arvot joillekin argumentin arvoille.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="(!LANG: Sinien ja kosinien taulukko" title="Taulukko sinit ja kosinit" ]!}

Lausekkeet monimutkaisten muuttujien kautta

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Eulerin kaava

\(e^(iz) = \cos z + i \sin z \)

Hyperbolisten funktioiden lausekkeet

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Johdannaiset

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Kaavojen johtaminen >>>

N:nnen kertaluvun johdannaiset:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Integraalit

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Katso myös kohta Epämääräisten integraalien taulukko >>>

Laajennukset sarjoiksi

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Sekantti, kosekantti

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

Käänteiset funktiot

Sinin ja kosinin käänteisfunktiot ovat vastaavasti arsini ja arkosiini.

Arcsine, arcsin

\(y = \arcsin x \) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

Arccosine, arccos

\(y = \arccos x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Viitteet:
SISÄÄN. Bronstein, K.A. Semendyaev, Matematiikan käsikirja insinööreille ja korkeakouluopiskelijoille, Lan, 2009.

Javascript on poistettu käytöstä selaimessasi.
ActiveX-komponentit on otettava käyttöön, jotta voit tehdä laskelmia!

Keskitetty pisteeseen A.
α on radiaaneina ilmaistu kulma.

Tangentti ( tgα) on trigonometrinen funktio, joka riippuu suorakulmaisen kolmion hypotenuusan ja haaran välisestä kulmasta α, joka on yhtä suuri kuin vastakkaisen haaran pituuden suhde |BC| viereisen haaran pituuteen |AB| .

Kotangentti ( ctgα) on trigonometrinen funktio, joka riippuu suorakulmaisen kolmion hypotenuusan ja haaran välisestä kulmasta α, joka on yhtä suuri kuin viereisen haaran pituuden suhde |AB| vastakkaisen jalan pituuteen |BC| .

Tangentti

Missä n-kokonainen.

Länsimaisessa kirjallisuudessa tangenttia merkitään seuraavasti:
.
;
;
.

Tangenttifunktion kuvaaja, y = tg x

Kotangentti

Missä n-kokonainen.

Länsimaisessa kirjallisuudessa kotangentti merkitään seuraavasti:
.
Myös seuraava merkintä on otettu käyttöön:
;
;
.

Kotangenttifunktion kuvaaja, y = ctg x


Tangentin ja kotangentin ominaisuudet

Jaksoisuus

Funktiot y= tg x ja y= ctg x ovat jaksollisia jaksolla π.

Pariteetti

Funktiot tangentti ja kotangentti ovat parittomia.

Määritelmä- ja arvoalueet, nouseva, laskeva

Funktiot tangentti ja kotangentti ovat jatkuvia määrittelyalueellaan (katso jatkuvuuden todiste). Tangentin ja kotangentin pääominaisuudet on esitetty taulukossa ( n- kokonaisluku).

y= tg x y= ctg x
Laajuus ja jatkuvuus
Arvoalue -∞ < y < +∞ -∞ < y < +∞
Nouseva -
Laskeva -
Äärimmäisyydet - -
Nollat, y= 0
Leikkauspisteet y-akselin kanssa, x = 0 y= 0 -

Kaavat

Lausekkeet sinin ja kosinin suhteen

; ;
; ;
;

Kaavat summan ja erotuksen tangentille ja kotangentille



Muut kaavat ovat esimerkiksi helppoja saada

Tangenttien tulo

Tangenttien summan ja eron kaava

Tämä taulukko näyttää tangenttien ja kotangenttien arvot joillekin argumentin arvoille.

Lausekkeet kompleksilukuina

Hyperbolisten funktioiden lausekkeet

;
;

Johdannaiset

; .


.
N:nnen kertaluvun johdannainen funktion muuttujan x suhteen:
.
Tangentin > > > kaavojen johtaminen ; kotangentille >>>

Integraalit

Laajennukset sarjoiksi

Saadaksesi tangentin laajennuksen potenssien x, sinun on otettava useita funktioiden laajennuksen termejä potenssisarjassa synti x ja cos x ja jakaa nämä polynomit toisiinsa , . Tämä johtaa seuraaviin kaavoihin.

klo .

osoitteessa .
missä B n- Bernoullin numerot. Ne määritetään joko toistuvuussuhteesta:
;
;
missä .
Tai Laplacen kaavan mukaan:


Käänteiset funktiot

Tangentin ja kotangentin käänteisfunktiot ovat vastaavasti arctangentti ja arkotangentti.

Arktangentti, arktg


, missä n-kokonainen.

Kaaretangentti, arcctg


, missä n-kokonainen.

Viitteet:
SISÄÄN. Bronstein, K.A. Semendyaev, Matematiikan käsikirja insinööreille ja korkeakouluopiskelijoille, Lan, 2009.
G. Korn, Matematiikan käsikirja tutkijoille ja insinööreille, 2012.

Keskitetty johonkin pisteeseen A.
α on radiaaneina ilmaistu kulma.

Määritelmä
Sinus on trigonometrinen funktio, joka riippuu suorakulmaisen kolmion hypotenuusan ja haaran välisestä kulmasta α, joka on yhtä suuri kuin vastakkaisen haaran pituuden suhde |BC| hypotenuusan pituuteen |AC|.

Kosini (cos α) on trigonometrinen funktio, joka riippuu suorakulmaisen kolmion hypotenuusan ja haaran välisestä kulmasta α, joka on yhtä suuri kuin viereisen haaran pituuden suhde |AB| hypotenuusan pituuteen |AC|.

Hyväksytyt nimitykset

;
;
.

;
;
.

Sinifunktion kuvaaja, y = sin x

Kosinifunktion kuvaaja, y = cos x


Sinin ja kosinin ominaisuudet

Jaksoisuus

Funktiot y= synti x ja y= cos x jaksollinen jaksolla 2 pi.

Pariteetti

Sinifunktio on outo. Kosinifunktio on parillinen.

Määritelmäalue ja arvot, äärimmäisyydet, lisäys, lasku

Sini- ja kosinifunktiot ovat jatkuvia määritelmäalueellaan, eli kaikille x:ille (katso jatkuvuuden todiste). Niiden tärkeimmät ominaisuudet on esitetty taulukossa (n - kokonaisluku).

y= synti x y= cos x
Laajuus ja jatkuvuus - ∞ < x < + ∞ - ∞ < x < + ∞
Arvoalue -1 ≤ y ≤ 1 -1 ≤ y ≤ 1
Nouseva
Laskeva
Maksimit, y= 1
Minimi, y = - 1
Nollat, y= 0
Leikkauspisteet y-akselin kanssa, x = 0 y= 0 y= 1

Peruskaavat

Sinin ja kosinin neliösumma

Sini- ja kosinikaavat summalle ja erolle



;
;

Kaavat sinien ja kosinien tulolle

Summa- ja erotuskaavat

Sinin ilmaisu kosinin kautta

;
;
;
.

Kosinin ilmaus sinin kautta

;
;
;
.

Ilmaisu tangentin suhteen

; .

Sille, meillä on:
; .

osoitteessa:
; .

Taulukko sinistä ja kosineista, tangenteista ja kotangenteista

Tämä taulukko näyttää sinien ja kosinien arvot joillekin argumentin arvoille.

Lausekkeet monimutkaisten muuttujien kautta


;

Eulerin kaava

Hyperbolisten funktioiden lausekkeet

;
;

Johdannaiset

; . Kaavojen johtaminen >>>

N:nnen kertaluvun johdannaiset:
{ -∞ < x < +∞ }

Sekantti, kosekantti

Käänteiset funktiot

Sinin ja kosinin käänteisfunktiot ovat vastaavasti arsini ja arkosiini.

Arcsine, arcsin

Arccosine, arccos

Viitteet:
SISÄÄN. Bronstein, K.A. Semendyaev, Matematiikan käsikirja insinööreille ja korkeakouluopiskelijoille, Lan, 2009.