Властивості синуса та його графік. Властивості синуса, косинуса, тангенсу та котангенсу

У цій статті ми покажемо, як даються визначення синуса, косинуса, тангенсу та котангенсу кута та числа в тригонометрії. Тут ми поговоримо про позначення, наведемо приклади записів, дамо графічні ілюстрації. На закінчення проведемо паралель між визначеннями синуса, косинуса, тангенсу та котангенсу в тригонометрії та геометрії.

Навігація на сторінці.

Визначення синуса, косинуса, тангенсу та котангенсу

Простежимо за тим, як формуються уявлення про синус, косінус, тангенс і котангенс в шкільному курсі математики. На уроках геометрії дається визначення синуса, косинуса, тангенсу та котангенсу гострого кута у прямокутному трикутнику. А пізніше вивчається тригонометрія, де йдеться про синус, косінус, тангенс і котангенс кута повороту і числа. Наведемо всі ці визначення, наведемо приклади та дамо необхідні коментарі.

гострого кута в прямокутному трикутнику

З курсу геометрії відомі визначення синуса, косинуса, тангенсу та котангенсу гострого кута у прямокутному трикутнику. Вони даються як відношення сторін прямокутного трикутника. Наведемо їх формулювання.

Визначення.

Синус гострого кута у прямокутному трикутнику- Це відношення протилежного катета до гіпотенузи.

Визначення.

Косинус гострого кута у прямокутному трикутнику- Це відношення прилеглого катета до гіпотенузи.

Визначення.

Тангенс гострого кута у прямокутному трикутнику- Це ставлення протилежного катета до прилеглого.

Визначення.

Котангенс гострого кута у прямокутному трикутнику- Це відношення прилеглого катета до протилежного.

Там же вводяться позначення синуса, косинуса, тангенсу та котангенсу – sin, cos, tg та ctg відповідно.

Наприклад, якщо АВС – прямокутний трикутник з прямим кутом З , то синус гострого кута A дорівнює відношенню протилежного катета BC до гіпотенузи AB , тобто sin A = BC / AB .

Ці визначення дозволяють обчислювати значення синуса, косинуса, тангенсу та котангенсу гострого кута за відомими довжинами сторін прямокутного трикутника, а також за відомими значеннями синуса, косинуса, тангенсу, котангенсу та довжиною однієї зі сторін знаходити довжини інших сторін. Наприклад, якби знали, що у прямокутному трикутнику катет AC дорівнює 3 , а гіпотенуза AB дорівнює 7 , ми могли б обчислити значення косинуса гострого кута A за визначенням: cos∠A=AC/AB=3/7 .

Кута повороту

У тригонометрії на кут починають дивитися ширше - вводять поняття кута повороту. Величина кута повороту, на відміну від гострого кута, не обмежена рамками від 0 до 90 градусів, кут повороту в градусах (і в радіанах) може виражатися будь-яким дійсним числом від −∞ до +∞ .

У цьому вся світлі дають визначення синуса, косинуса, тангенса і котангенса не гострого кута, а кута довільної величини - кута повороту. Вони даються через координати x і y точки A 1 , яку переходить так звана початкова точка A(1, 0) після її повороту на кут α навколо точки O – початку прямокутної декартової системи координат і центру одиничного кола .

Визначення.

Синус кута поворотуα - це ордината точки A 1 тобто sinα = y .

Визначення.

Косинусом кута поворотуα називають абсцис точки A 1 , тобто, cosα=x .

Визначення.

Тангенс кута поворотуα - це відношення ординати точки A 1 до її абсцис, тобто tgα=y/x.

Визначення.

Котангенсом кута поворотуα називають відношення абсциси точки A 1 до її ординати, тобто ctgα=x/y .

Синус і косинус визначені для будь-якого кута α, тому що ми завжди можемо визначити абсцис і ординату точки, яка виходить в результаті повороту початкової точки на кут α. А тангенс та котангенс визначені не для будь-якого кута. Тангенс не визначений для таких кутів α , при яких початкова точка перетворюється на точку з нульовою абсцисою (0, 1) або (0, −1) , а це має місце при кутах 90°+180°·k , k∈Z (π /2+π·k радий). Справді, за таких кутах повороту вираз tgα=y/x немає сенсу, оскільки у ньому присутній розподіл на нуль. Що ж до котангенса, то він не визначений для таких кутів α , при яких початкова точка переходить до точки з нульовою ординатою (1, 0) або (−1, 0) , а це має місце для кутів 180°·k , k ∈Z (π·k радий).

Отже, синус і косинус визначені для будь-яких кутів повороту, тангенс визначений для всіх кутів, крім 90°+180°·k , k∈Z (π/2+π·k рад), а котангенс – для всіх кутів, крім 180° ·k, k∈Z (π·k радий).

У визначеннях фігурують вже відомі нам позначення sin, cos, tg і ctg, вони використовуються і для позначення синуса, косинуса, тангенса та котангенсу кута повороту (іноді можна зустріти позначення tan та cot, що відповідають тангенсу та котангенсу). Так синус кута повороту 30 градусів можна записати як sin30° записам tg(−24°17′) і ctgα відповідають тангенс кута повороту −24 градуси 17 хвилин і котангенс кута повороту α . Нагадаємо, що при записі радіанної міри кута позначення "рад" часто опускають. Наприклад, косинус кута повороту в три піради зазвичай позначають cos3·π.

На закінчення цього пункту варто зазначити, що у розмові про синус, косинус, тангенс і котангенс кута повороту часто опускають словосполучення кут повороту або слово повороту. Тобто замість фрази «синус кута повороту альфа» зазвичай використовують фразу «синус кута альфа» або ще коротше – «синус альфа». Це стосується і косинуса, і тангенса, і котангенса.

Також скажемо, що визначення синуса, косинуса, тангенса і котангенса гострого кута в прямокутному трикутнику узгоджуються з щойно даними визначеннями синуса, косинуса, тангенса і котангенса кута повороту величиною від 0 до 90 градусів. Це ми обґрунтуємо.

Числа

Визначення.

Синусом, косинусом, тангенсом та котангенсом числа t називають число, що дорівнює синусу, косинусу, тангенсу та котангенсу кута повороту в t радіанів відповідно.

Наприклад, косинус числа 8 π за визначенням є число, рівне косинусу кута в 8 π рад. А косинус кута в 8 π рад дорівнює одиниці, тому, косинус числа 8 π дорівнює 1 .

Існує й інший підхід до визначення синуса, косинуса, тангенсу та котангенсу числа. Він полягає в тому, що кожному дійсному числу t ставиться у відповідність точка одиничного кола з центром на початку прямокутної системи координат, синус, косинус, тангенс і котангенс визначаються через координати цієї точки. Зупинимося на цьому детальніше.

Покажемо, як встановлюється відповідність між дійсними числами та точками кола:

• числу 0 ставиться у відповідність початкова точка A(1, 0);
• позитивному числу t ставиться у відповідність точка одиничного кола, в яке ми потрапимо, якщо рухатимемося по колу з початкової точки в напрямку проти годинникової стрілки і пройдемо шлях довжиною t;
• негативному числу t ставиться у відповідність точка одиничного кола, в яке ми потрапимо, якщо рухатимемося по колу з початкової точки в напрямку за годинниковою стрілкою і пройдемо шлях довжиною | t | .

Тепер переходимо до визначення синусу, косинуса, тангенсу і котангенсу числа t . Припустимо, що t відповідає точка кола A 1 (x, y) (наприклад, числу &pi/2; відповідає точка A 1 (0, 1) ).

Визначення.

Синусом числа t називають ординату точки одиничного кола, що відповідає числу t, тобто, sint = y.

Визначення.

Косинусом числа t називають абсцису точки одиничного кола, що відповідає числу t, тобто, cost = x.

Визначення.

Тангенсом числа t називають відношення ординати до абсцисі точки одиничного кола, що відповідає числу t, тобто, tgt=y/x. В іншому рівносильному формулюванні тангенс числа t - це відношення синуса цього числа до косинусу, тобто tgt = sint / cost.

Визначення.

Котангенсом числа t називають відношення абсциси до ординати точки одиничного кола, що відповідає числу t, тобто ctgt=x/y . Інше формулювання таке: тангенс числа t – це відношення косинуса числа t до синуса числа t: ctgt=cost/sint.

Тут відзначимо, що дані визначення узгоджуються з визначенням, даним на початку цього пункту. Дійсно, точка одиничного кола, що відповідає числу t збігається з точкою, отриманої в результаті повороту початкової точки на кут в t радіанів.

Ще варто прояснити такий момент. Допустимо, перед нами запис sin3 . Як зрозуміти, про синус числа 3 або про синус кута повороту в 3 радіана йдеться? Зазвичай це ясно з контексту, інакше це, швидше за все, не має принципового значення.

Тригонометричні функції кутового та числового аргументу

Згідно з даними в попередньому пункті визначенням, кожному куті повороту відповідають цілком певне значення sinα, як і значення cosα. Крім того, всім кутам повороту, відмінним від 90°+180°·k , k∈Z (π/2+π·k рад) відповідають значення tgα , а відмінним від 180°·k , k∈Z (π·k рад ) – значення ctgα. Тому sinα, cosα, tgα та ctgα - це функції кута α. Інакше кажучи – це функції кутового аргумента.

Аналогічно можна говорити про функції синус, косинус, тангенс і котангенс числового аргументу. Справді, кожному дійсному числу t відповідає цілком певне значення sint, як і cost. Крім того, усім числам, відмінним від π/2+π·k , k∈Z відповідають значення tgt , а числам π·k , k∈Z - значення ctgt .

Функції синус, косинус, тангенс та котангенс називають основними тригонометричними функціями.

З контексту зазвичай зрозуміло, з тригонометричними функціями кутового аргументу чи числового аргументу ми маємо справу. Інакше ми можемо вважати незалежну змінну як мірою кута (кутовим аргументом), і числовим аргументом.

Проте, у школі переважно вивчаються числові функції, тобто, функції, аргументи яких, як і відповідні їм значення функції, є числами. Тому якщо йдеться саме про функції, то доцільно вважати тригонометричні функції функціями числових аргументів.

Зв'язок визначень з геометрії та тригонометрії

Якщо розглядати кут повороту величиною від 0 до 90 градусів, то дані в контексті тригонометрії визначення синуса, косинуса, тангенса і котангенса кута повороту повністю узгоджуються з визначеннями синуса, косинуса, тангенса і котангенса гострого кута в прямокутному трикутнику, які даються в курсі геометр. Обґрунтуємо це.

Зобразимо у прямокутній декартовій системі координат Oxy одиничне коло. Зазначимо початкову точку A(1, 0). Повернемо її на кут величиною від 0 до 90 градусів, отримаємо точку A 1 (x, y) . Опустимо з точки А 1 на вісь Ox перпендикуляр A 1 H.

Легко бачити, що в прямокутному трикутнику кут A 1 OH дорівнює куту повороту α , довжина катета OH, що прилягає до цього кута, дорівнює абсцисі точки A 1 , тобто, |OH|=x , довжина протилежного до кута катета A 1 H дорівнює ординаті точки A 1 , тобто, |A 1 H|=y , а довжина гіпотенузи OA 1 дорівнює одиниці, оскільки є радіусом одиничного кола. Тоді за визначенням з геометрії синус гострого кута в прямокутному трикутнику A 1 OH дорівнює відношенню протилежного катета до гіпотенузи, тобто, sinα=|A 1 H|/|OA 1 |=y/1=y . А за визначенням із тригонометрії синус кута повороту дорівнює ординаті точки A 1 , тобто, sinα=y . Звідси видно, що визначення синуса гострого кута у прямокутному трикутнику еквівалентне визначенню синуса кута повороту α при α від 0 до 90 градусів.

Аналогічно можна показати, що визначення косинуса, тангенса і котангенса гострого кута α узгоджуються з визначеннями косинуса, тангенса і котангенса кута повороту α .

Список літератури.

1. Геометрія. 7-9 класи: навч. для загальноосвіт. установ/[Л. З. Атанасян, У. Ф. Бутузов, З. Б. Кадомцев та інших.]. - 20-те вид. М.: Просвітництво, 2010. – 384 с.: іл. - ISBN 978-5-09-023915-8.
2. Погорєлов А. В.Геометрія: Навч. для 7-9 кл. загальноосвіт. установ/ А. В. Погорелов. - 2-ге вид - М.: Просвітництво, 2001. - 224 с.: іл. - ISBN 5-09-010803-X.
3. Алгебра та елементарні функції: Навчальний посібник для учнів 9 класу середньої школи/Є. С. Кочетков, Є. С. Кочеткова; За редакцією доктора фізико-математичних наук О. Н. Головіна. - 4-те вид. М: Просвітництво, 1969.
4. Алгебра:Навч. для 9 кл. середовищ. шк./Ю. Н. Макарічев, Н. Г. Міндюк, К. І. Нешков, С. Б. Суворова; За ред. З. А. Теляковського.- М.: Просвітництво, 1990.- 272 з.: ил.- ISBN 5-09-002727-7
5. Алгебрата початку аналізу: Навч. для 10-11 кл. загальноосвіт. установ / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудніцин та ін; За ред. А. Н. Колмогорова. - 14-те вид. - М.: Просвітництво, 2004. - 384 с.: Іл. - ISBN 5-09-013651-3.
6. Мордковіч А. Г.Алгебра та початку аналізу. 10 клас. У 2 год. Ч. 1: підручник для загальноосвітніх закладів (профільний рівень)/ А. Г. Мордкович, П. В. Семенов. - 4-те вид., Дод. – М.: Мнемозіна, 2007. – 424 с.: іл. ISBN 978-5-346-00792-0.
7. Алгебрата початку математичного аналізу. 10 клас: навч. для загальноосвіт. установ: базовий та профіл. рівні/[Ю. М. Колягін, М. В. Ткачова, Н. Є. Федорова, М. І. Шабунін]; за ред. А. Б. Жижченко. - 3-тє вид. – І.: Просвітництво, 2010. – 368 с.: іл. – ISBN 978-5-09-022771-1.
8. Башмаков М. І.Алгебра та початку аналізу: Навч. для 10-11 кл. середовищ. шк. - 3-тє вид. - М: Просвітництво, 1993. - 351 с.: іл. - ISBN 5-09-004617-4.
9. Гусєв В. А., Мордкович А. Г.Математика (посібник для вступників у технікуми): Навч. посібник.- М.; Вищ. шк., 1984.-351 с., іл.

З графіків видно що:

1. Графіки синуса та косинуса коливаються в межах між -1 та 1
2. Крива косинуса має ту саму форму, що й крива синуса, але зсунута щодо неї на 90 o
3. Криві синуса та косинуса безперервні та повторюються з періодом 360 o , крива тангенсу має розриви та повторюється з періодом 180 o .

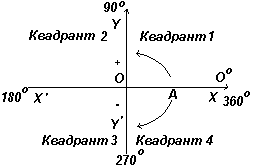На рис. зліва показані перпендикулярні осі ХХ" та YY"; що перетинаються на початку координат О. При роботі з графіками вимірювання вправо і вгору від Про вважаються позитивними, ліворуч і вниз від Про - негативними. Нехай ОА вільно обертається щодо О. При повороті ОА проти годинникової стрілки кут, що вимірюється, вважається позитивним, а при повороті за годинниковою стрілкою - негативним.

Графік. Позитивне чи негативне
напрямок при русі по колу.

Нехай ОА обертається проти годинникової стрілки таким чином, що 1 - будь-який кут у першому квадранті, і побудуємо перпендикуляр АВ для отримання прямокутного трикутника ОАВ на рис. ліворуч. Оскільки всі три сторони трикутника є позитивними, тригонометричні функції синус, косинус і тангенс у першому квадранті будуть позитивні. (Зазначимо, що довжина ОА завжди є позитивною, оскільки є радіусом кола.)
Нехай ОА обертається далі таким чином, що 2 - будь-який кут у другому квадранті, і побудуємо АС так, щоб утворився прямокутний трикутник ОАС. Тоді sin 2 =+/+ = +; cos 2 =+/- = -; tg 2 =+/- = -. Нехай ОА обертається далі таким чином, що 3 - будь-який кут у третьому квадранті і побудуємо АD так, щоб утворився прямокутний трикутник ОАD. Тоді sin 3 = -/+ = -; cos 3 = -/+ = -; tg 3 = -/- =+ .

Графік. Побудова кутів у
різних квадрантів.

Нехай ОА обертається далі таким чином, що 4 - будь-який кут у четвертому квадранті, і побудуємо АЕ так, щоб утворився прямокутний трикутник ОАЕ. Тоді sin 4 = -/+= -; cos Θ 4 =+/+=+; tg 4 = -/+= -.

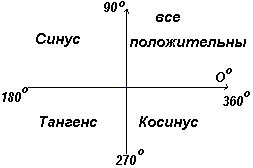
У першому квадранті всі тригонометричні функції мають позитивні значення, у другому позитивний лише синус, у третьому - лише тангенс, у четвертому лише косинус, що й показано на рис. ліворуч.

Знання кутів довільної величини необхідно при знаходженні, наприклад, всіх кутів між 0 o і 360 o синус яких дорівнює, скажімо, 0,3261. Якщо ввести калькулятор 0,3261 і натиснути кнопку sin -1 , отримаємо відповідь 19,03 o . Однак існує другий кут між 0 o і 360 o який калькулятор не покаже. Синус також позитивний у другому квадранті. Інший кут показано на рис. нижче як кут Θ, де Θ=180 o - 19,03 o = 160,97 o . Таким чином, 19,03 o і 160,97 o - це кути в діапазоні від 0 o до 360 o синус яких дорівнює 0,3261.

Будьте уважні! Калькулятор дає лише одне з цих значень. Друге значення слід визначити згідно з теорією кутів довільної величини.

Приклад 1

Знайти всі кути в діапазоні від 0 o до 360 o , синус яких дорівнює -0,7071

Рішення:
Кути, синус яких дорівнює -0,7071 o знаходяться в третьому та четвертому квадранті, оскільки синус негативний у цих квадрантах (див. мал. зліва).

Графік. Знаходження всіх кутів по
заданому значенню синуса (приклад)

З наступного малюнка Θ = arcsin 0,7071 = 45 o. Два кути в діапазоні від 0 o до 360 o, синус яких дорівнює -0,7071, це 180 o +45 o =225 o і 360 o - 45 o = 315 o.

Примітка.Калькулятор дає лише одну відповідь.
Графік. Знаходження всіх кутів по
заданому значенню синуса (приклад)

Приклад 2

Знайти всі кути між 0 o і 360 o тангенс яких дорівнює 1, 327.

Рішення:
Тангенс позитивний у першому та третьому квадрантах - рис. ліворуч.
Графік. Знаходження всіх кутів по

З рис нижче Θ = arctg1,327 = 53 o.
Два кути в діапазоні від 0 o до 360 o тангенс яких дорівнює 1,327, це 53 o і 180 o + 53 o , тобто. 233 o .
Графік. Знаходження всіх кутів по
заданому значенню тангенсу (приклад)

Нехай ОR на рис. ліворуч- це вектор одиничної довжини, що вільно обертається проти годинникової стрілки навколо О. За один оборот виходить коло, показаний на рис. і розділений секторами по 15 o. Кожен радіус має горизонтальну та вертикальну складову. Наприклад, для 30 o вертикальна складова - це TS, а горизонтальна - OS.

З визначення тригонометричних функцій
sin30 o = TS/TO = TS/1, тобто. TS = sin30 oі cos30 o =OS/TO=OS/1, тобто. OS=cos30 o

Вертикальну складову TS можна перенести на графік у вигляді T"S", що дорівнює значенню, що відповідає куту 30 o графіку залежності y від кута х. Якщо всі вертикальні складові, подібно до TS, перенести на графік, то вийде синусоїда, показана на рис. вище.

Якщо всі горизонтальні складові, подібні OS, спроектувати на графік залежності від кута х, вийде косинусоїда. Ці проекції легко візуалізувати, перемальовуючи коло з радіусом OR та початком відліку кутів від вертикалі, як показано на малюнку зліва.
З рис. ліворуч видно, що синусоїда має ту ж форму, що і косінусоїда, але зміщена на 90 o .

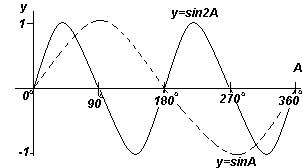Періодичні функції та період
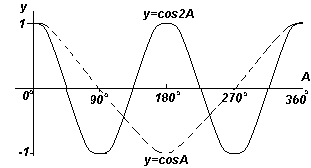
Кожен із графіків функцій, показаних на чотирьох рис. вище, повторюється зі збільшенням кута А, тому їх називають періодичними функціями.
Функції y=sinA та y=cosA повторюються через кожні 360 o (або 2π радіан), тому 360 o називається періодомцих функцій. Функції y = sin2A і y = cos2A повторюються через кожні 180 o (або π радіан), тому 180 o - це період для даних функцій.
У випадку якщо y=sinpA і y=cospA (де р - константа), то період функції дорівнює 360 o /p (або 2π/p радіан). Отже, якщо y=sin3A, то період цієї функції дорівнює 360 o /3= 120 o якщо y=cos4A, то період цієї функції дорівнює 360 o /4= 90 o .

Амплітуда
Амплітудоюназивається максимальне значення синусоїди. Кожен із графіків 1-4 має амплітуду +1 (тобто вони коливаються між +1 та -1). Однак, якщо y=4sinA, кожна з величин sinA множиться на 4, таким чином, максимальна величина амплітуди - 4. Аналогічно для y=5cos2A амплітуда дорівнює 5, а період - 360 o /2 = 180 o .

Приклад 3.
Побудувати y=3sin2A в діапазоні від А=0 o до А=360 o.

Рішення:
Амплітуда = 3, період = 360 o /2 = 180 o.

Приклад 4.
Побудувати графік y=4cos2x у діапазоні від х=0 o до х=360 o

Рішення:
Амплітуда = 4. період = 360 o /2 = 180 o.

Кути запізнення та випередження
Криві синуса та косинуса не завжди починаються в 0 o . Щоб врахувати цю обставину, періодична функція представляється як y=sin(A± α), де α - зсув фази щодо y=sinA і y=cosA.

Склавши таблицю значень, можна побудувати графік функції y = sin (A-60 o), показаний на рис. ліворуч. Якщо крива y=sinA починається в 0 o , то крива y=sin(A-60 o) починається в 60 o (тобто її нульове значення на 60 o правіше). Таким чином, кажуть, що y=sin(A-60o) запізнюєтьсящодо y=sinA на 60 o .
Графік. y=sin(A-60 o) (синусоїда).

Склавши таблицю значень, можна побудувати графік функції y = cos (A + 45 o), показаний на рис. нижче.
Якщо крива y=cosA починається в 0 o , то крива y=cos(A+45 o) починається на 45 o лівіше (тобто її нульова величина знаходиться на 45 o раніше).
Таким чином, кажуть, що графік y = cos (A + 45 o) випереджаєграфік y=cosA на 45 o .
Графік. y=cos(A+45 o) (косинусоїда).

Загалом, графік y=sin(A-α) запізнюється щодо y=sinAна кут α.
Косинусоида має таку форму, як і синусоїда, але починається на 90 o лівіше, тобто. випереджає її на 90 o. Отже, cosA=sin(A+90 o).

Приклад 5.
Побудувати графік y=5sin(A+30 o) у діапазоні від А=0 o до А=360 o

Рішення:
Амплітуда = 5, період = 360 o /1 = 360 o.
5sin(A+30 o) випереджає 5sinA на 30 o тобто. починається на 30 o раніше.
Графік y=5sin(A+30 o) (синусоїда).

Приклад 6.
Побудувати графік y=7sin(2A-π/3) у діапазоні від А=0 o до А=360 o .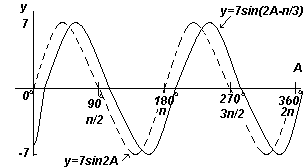

Рішення:
Амплітуда = 7, період = 2π/2 = π радіан
У загальному випадку y=sin(pt-α) запізнюється щодо y=sinpt на α/p, Отже 7sin(2A-π/3) запізнюється щодо 7sin2A на (π/3)/2, тобто. на π/6 радіан або на 30 o

Синусоїда виду Asin(ωt±α). Фазовий кут. Зрушення по фазі.

Нехай OR на мал. ліворуч являє собою вектор, що вільно обертається проти годинникової стрілки навколо Про зі швидкістю радіан/с. Вектор, що обертається, називається фазовим вектором. Через час t секунд OR повернеться на кут t радіан (на рис. зліва це кут TOR). Якщо перпендикулярно OR побудувати ST, то sinωt=ST/OT, тобто. ST=OTsinωt.
Якщо всі подібні вертикальні складові спроектувати на графік залежності від ωt, вийде синусоїда з амплітудою OR.

Якщо фазовий вектор OR робить один оборот (тобто 2π радіан) за Т секунд, то кутова швидкість ω=2π/Т рад/с, звідки
Т=2π/ω (с), де
Т – це період
Число повних періодів, що проходять за 1 секунду, називається частотою f.
Частота = (кількість періодів)/(секунда) = 1/ T = ω/2π Гц,тобто. f= ω/2π Гц
Отже, кутова швидкість
ω=2πf рад/с.

Якщо у загальному вигляді синусоїдальна функція виглядає як y=sin(ωt± α), то
А – амплітуда
ω - кутова швидкість
2π/ ω - період Т, с
ω/2π - частота f, Гц
α - кут випередження або запізнення (щодо y=Аsinωt) у радіанах, він називається також фазовим кутом.

Приклад 7.
Змінний струм визначається як i=20sin(90πt+0,26) ампер. Визначити амплітуду, період, частоту та фазовий кут (у градусах)

Рішення:
i=20sin(90πt+0,26)А, отже,
амплітуда дорівнює 20 А
кутова швидкість ω=90π, отже,
період Т= 2π/ω = 2π/ 90π = 0,022 с = 22мс
частота f= 1/Т = 1/0,022 = 45,46 Гц
фазовий кут α= 0,26 рад. = (0,26 * 180/π) o = 14,9 o.

Приклад 8.
Коливальний механізм має максимальне усунення 3 м і частоту 55 Гц. Під час t=0 усунення становить 100см. Виразити зсув у загальному вигляді Аsin(ωt±α).

Рішення
Амплітуда = максимальне усунення = 3м
Кутова швидкість ω=2πf = 2π(55) = 110 πрад./с
Отже, усунення 3sin(110πt + α) м.
При t=0 усунення = 100см=1м.
Отже, 1 = 3sin (0 + α), тобто. sinα=1/3=0,33
Отже α=arcsin0,33=19 o
Отже, усунення дорівнює 3sin(110 πt + 0,33).

Приклад 9.
Значення миттєвого напруження у схемі змінного струму у будь-які t секунд задається у вигляді v=350sin(40πt-0,542)В. Знайти:
а) Амплітуду, період, частоту та фазовий кут (у градусах)
б) значення напруги за t =0
в) значення напруги при t = 10 мс
г) час, протягом якого напруга вперше досягне значення 200 В.
Рішення:
а) Амплітуда дорівнює 350 В, кутова швидкість дорівнює ω=40π
Отже,
період Т=2π/ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовий кут = 0,542 рад (0,542*180/π) = 31 o із запізненням щодо v=350sin(40πt)
б) Якщо t =0, то v=350sin(0-0,542)=350sin(-31 o)=-180,25 В
в) Якщо t =10 мс, то v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6 В
г) Якщо v=200 І, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

Графік. Коливальний механізм
(Приклад, синусоїда).

v=350sin(40πt-0,542) Отже, (40πt-0,542)=arcsin200/350=35 o або 0,611 рад.
40πt = 0,611 +0,542 = 1,153.
Отже, якщо v=200В, час t=1,153/40π=9,179 мс

Геометричне визначення синуса та косинуса

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α - Кут, виражений у радіанах.

Сінус (sin α)– це тригонометрична функція від кута α між гіпотенузою та катетом прямокутного трикутника, що дорівнює відношенню довжини протилежного катета |BC| до довжини гіпотенузи | AB |.

Косинус (cos α)– це тригонометрична функція від кута α між гіпотенузою та катетом прямокутного трикутника, що дорівнює відношенню довжини прилеглого катета |AC| до довжини гіпотенузи | AB |.

Тригонометричне визначення

За допомогою формул, зазначених вище, можна знайти синус та косинус гострого кута. Але треба навчитися обчислювати синус та косинус кута довільної величини. Прямокутний трикутник не дає такої можливості (тупого кута, наприклад, у ньому не може бути); отже, потрібно загальне визначення синуса і косинуса, що містить зазначені формули як окремий випадок.

На допомогу приходить тригонометричне коло. Нехай дано певний кут; йому відповідає однойменна точка на тригонометричному колі.

Рис. 2. Тригонометричне визначення синуса та косинуса

Косинус кута - це абсцис точки. Синус кута – це ордината точки.

На рис. 2 кут взятий гострим, і легко зрозуміти, що це визначення збігається із загальним геометричним визначенням. Справді, бачимо прямокутний трикутник з одиничною гіпотенузою O і гострим кутом. Прилеглий катет цього трикутника є cos (порівняйте з рис. 1) і одночасно абсцис точки; протилежний катет є sin (як на рис. 1) та одночасно ордината точки.

Але тепер ми вже не обмежені першою чвертю і отримуємо можливість поширити це визначення на будь-який кут. На рис. 3 показано, що таке синус і косинус кута у другій, третій та четвертій чвертях.

Рис. 3. Синус та косинус у II, III та IV чвертях

Табличні значення синуса та косинуса

Нульовий кут \(\LARGE 0^(\circ ) \)

Абсцис точки 0 дорівнює 1 , ордината точки 0 дорівнює 0 . Отже,

cos 0 = 1 sin 0 = 0

Рис 4. Нульовий кут

Кут \(\LARGE \frac(\pi)(6) = 30^(\circ ) \)

Ми бачимо прямокутний трикутник з одиничною гіпотенузою та гострим кутом 30°. Як відомо, катет, що лежить навпроти кута 30° дорівнює половині гіпотенузи 1 ; інакше кажучи, вертикальний катет дорівнює 1/2 і, отже,

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Горизонтальний катет знаходимо по теоремі Піфагора (або, що те саме, знаходимо косинус за основною тригонометричною тотожністю):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 ) \]

1 Чому так виходить? Розріжте рівносторонній трикутник зі стороною 2 вздовж його висоти! Він розпадеться на два прямокутні трикутники з гіпотенузою 2, гострим кутом 30° і меншим катетом 1.

Рис 5. Кут π/6

Кут \(\LARGE \frac(\pi)(4) = 45^(\circ ) \)

У цьому випадку прямокутний трикутник є рівнобедреним; синус і косинус кута 45 ° дорівнюють один одному. Позначимо їх поки що через x . Маємо:

\[ x^(2) + x^(2) = 1 \]

звідки \(x=\frac(\sqrt(2) )(2) \). Отже,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Рис 5. Кут π/4

Властивості синуса та косинуса

Прийняті позначення

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Періодичність

Функції y = sin x та y = cos x періодичні з періодом 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Парність

Функція синус – непарна. Функція косинус – парна.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Області визначення та значень, екстремуми, зростання, спадання

Основні властивості синуса та косинуса представлені в таблиці ( n- ціле).

	\(\small< x < \)	\(\small -\pi + 2\pi n \) \(\small< x < \) \(\small 2\pi n \)
Зменшення	\(\small \dfrac(\pi)2 + 2\pi n \)\(\small< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \)	\(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \)
Максимуми, \(\small x = \) \(\small \dfrac(\pi)2 + 2\pi n \)	\(\small x = 2\pi n \)
Мінімуми, \(\small x = \) \(\small -\dfrac(\pi)2 + 2\pi n \)	\(\small x = \) \(\small \pi + 2\pi n \)
Нулі, \(\small x = \pi n \)	\(\small x = \dfrac(\pi)2 + \pi n \)
Крапки перетину з віссю ординат, x = 0	y = 0	y = 1

Основні формули, що містять синус та косинус

Сума квадратів

\(\sin^2 x + \cos^2 x = 1 \)

Формули синуса та косинуса суми та різниці

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \); \(\sin(x + \pi) = - \sin x \)

Формули твору синусів та косінусів

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large )) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large )) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large )) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large )) \)

Формули суми та різниці

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Вираз синуса через косинус

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Вираз косинуса через синус

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Вираз через тангенс

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

При \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

При \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Таблиця синусів та косінусів, тангенсів та котангенсів

У цій таблиці представлені значення синусів і косінусів при деяких значеннях аргументу.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="(!LANG:Таблиця синусів та косінусів" title="Таблиця синусів та косінусів" ]!}

Вирази через комплексні змінні

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Формула Ейлера

\(e^(iz) = \cos z + i \sin z \)

Вирази через гіперболічні функції

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Похідні

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Висновок формул > > >

Похідні n-го порядку:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Інтеграли

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
також розділ Таблиця невизначених інтегралів >>>

Розкладання до лав

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Секанс, косеканс

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

Зворотні функції

Зворотними функціями до синуса і косінус є арксинус і арккосинус, відповідно.

Арксинус, arcsin

\(y = \arcsin x \) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

Арккосинус, arccos

\(y = \arccos x \) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Використана література:
І.М. Бронштейн, К.А. Семендяєв, Довідник з математики для інженерів та учнів втузів, «Лань», 2009.

У вашому браузері вимкнено Javascript.
Щоб розрахувати, необхідно дозволити елементи ActiveX!

З центром у точці A .
α – кут, виражений у радіанах.

Тангенс ( tg α) - це тригонометрична функція, що залежить від кута між гіпотенузою і катетом прямокутного трикутника, рівна відношенню довжини протилежного катета |BC| до довжини прилеглого катета | AB | .

Котангенс ( ctg α) - це тригонометрична функція, що залежить від кута між гіпотенузою і катетом прямокутного трикутника, рівна відношенню довжини прилеглого катета |AB| до довжини протилежного катета | BC | .

Тангенс

Де n- ціле.

У західній літературі тангенс позначається так:
.
;
;
.

Графік функції тангенсу, y = tg x

Котангенс

Де n- ціле.

У західній літературі котангенс позначається так:
.
Також прийнято такі позначення:
;
;
.

Графік функції котангенсу, y = ctg x

Властивості тангенсу та котангенсу

Періодичність

Функції y = tg xта y = ctg xперіодичні з періодом π.

Парність

Функції тангенс та котангенс - непарні.

Області визначення та значень, зростання, спадання

Функції тангенс і котангенс безперервні у своїй області визначення (див. доказ безперервності). Основні властивості тангенсу та котангенсу представлені в таблиці ( n- ціле).

	y = tg x	y = ctg x
Область визначення та безперервність
Область значень	-∞ < y < +∞	-∞ < y < +∞
Зростання		-
Зменшення	-
Екстремуми	-	-
Нулі, y = 0
Крапки перетину з віссю ординат, x = 0	y = 0	-

Формули

Вирази через синус та косинус

; ;
; ;
;

Формули тангенсу та котангенс від суми та різниці

Інші формули легко отримати, наприклад

Твір тангенсів

Формула суми та різниці тангенсів

У цій таблиці представлені значення тангенсів та котангенсів при деяких значеннях аргументу.

Вирази через комплексні числа

Вирази через гіперболічні функції

;
;

Похідні

; .

.
Похідна n-го порядку змінної x від функції :
.
Виведення формул для тангенсу >>>; для котангенсу > > >

Інтеграли

Розкладання до лав

Щоб отримати розкладання тангенсу за ступенями x, потрібно взяти кілька членів розкладання в степеневий ряд для функцій sin xі cos xі розділити ці багаточлени один на одного. При цьому виходять такі формули.

При .

при .
де B n- Числа Бернуллі. Вони визначаються або з рекурентного співвідношення:
;
;
де.
Або за формулою Лапласа:

Зворотні функції

Зворотними функціями до тангенсу та котангенсу є арктангенс та арккотангенс відповідно.

Арктангенс, arctg

, де n- ціле.

Арккотангенс, arcctg

, де n- ціле.

Використана література:
І.М. Бронштейн, К.А. Семендяєв, Довідник з математики для інженерів та учнів втузів, «Лань», 2009.
Г. Корн, Довідник з математики для науковців та інженерів, 2012.

З центром у точці A.
α - Кут, виражений у радіанах.

Визначення
Сінус (sin α)- це тригонометрична функція, що залежить від кута між гіпотенузою і катетом прямокутного трикутника, рівна відношенню довжини протилежного катета |BC| до довжини гіпотенузи | AC |

Косинус (cos α)- це тригонометрична функція, що залежить від кута між гіпотенузою і катетом прямокутного трикутника, рівна відношенню довжини прилеглого катета |AB| до довжини гіпотенузи | AC |

Прийняті позначення

;
;
.

;
;
.

Графік функції синус, y = sin x

Графік функції косинус, y = cos x

Властивості синуса та косинуса

Періодичність

Функції y = sin xта y = cos xперіодичні з періодом 2 π.

Парність

Функція синус – непарна. Функція косинус – парна.

Область визначення та значень, екстремуми, зростання, спадання

Функції синус і косинус безперервні у своїй області визначення, тобто всім x (див. доказ безперервності). Їхні основні властивості представлені в таблиці (n - ціле).

	y = sin x	y = cos x
Область визначення та безперервність	- ∞ < x < + ∞	- ∞ < x < + ∞
Область значень	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Зростання
Зменшення
Максимуми, y = 1
Мінімуми, y = - 1
Нулі, y = 0
Крапки перетину з віссю ординат, x = 0	y = 0	y = 1

Основні формули

Сума квадратів синуса та косинуса

Формули синуса та косинуса від суми та різниці

;
;

Формули твору синусів та косінусів

Формули суми та різниці

Вираз синуса через косинус

;
;
;
.

Вираз косинуса через синус

;
;
;
.

Вираз через тангенс

; .

При , маємо:
; .

При:
; .

Таблиця синусів та косінусів, тангенсів та котангенсів

У цій таблиці представлені значення синусів і косінусів при деяких значеннях аргументу.

Вирази через комплексні змінні

;

Формула Ейлера

Вирази через гіперболічні функції

;
;

Похідні

; . Висновок формул > > >

Похідні n-го порядку:
{ -∞ < x < +∞ }

Секанс, косеканс

Зворотні функції

Зворотними функціями до синуса і косинусу є арксинус і арккосинус відповідно.

Арксинус, arcsin

Арккосинус, arccos

Використана література:
І.М. Бронштейн, К.А. Семендяєв, Довідник з математики для інженерів та учнів втузів, «Лань», 2009.