Własności sinusa i jego wykres. Właściwości sinusa, cosinusa, tangensa i cotangensa

W tym artykule pokażemy jak definicje sinusa, cosinusa, tangensa i cotangensa kąta i liczby w trygonometrii. Tutaj porozmawiamy o notacji, podamy przykłady zapisów, podamy ilustracje graficzne. Podsumowując, rysujemy paralelę między definicjami sinusa, cosinusa, tangensa i cotangensa w trygonometrii i geometrii.

Nawigacja po stronach.

Definicja sinusa, cosinusa, tangensa i cotangensa

Prześledźmy, jak w szkolnym kursie matematyki powstaje pojęcie sinusa, cosinusa, tangensa i cotangensa. Na lekcjach geometrii podana jest definicja sinusa, cosinusa, tangensa i cotangensa kąta ostrego w trójkącie prostokątnym. A później badana jest trygonometria, która odnosi się do sinusa, cosinusa, tangensa i cotangensa kąta obrotu i liczby. Podajemy wszystkie te definicje, podajemy przykłady i podajemy niezbędne komentarze.

Kąt ostry w trójkącie prostokątnym

Z przebiegu geometrii znane są definicje sinusa, cosinusa, tangensa i cotangensa kąta ostrego w trójkącie prostokątnym. Są one podane jako stosunek boków trójkąta prostokątnego. Przedstawiamy ich formuły.

Definicja.

Sinus kąta ostrego w trójkącie prostokątnym jest stosunkiem przeciwnej nogi do przeciwprostokątnej.

Definicja.

Cosinus kąta ostrego w trójkącie prostokątnym to stosunek sąsiedniej nogi do przeciwprostokątnej.

Definicja.

Styczna do kąta ostrego w trójkącie prostokątnym jest stosunkiem nogi przeciwnej do nogi sąsiedniej.

Definicja.

Cotangens kąta ostrego w trójkącie prostokątnym jest stosunkiem nogi sąsiedniej do nogi przeciwnej.

Wprowadzono tam również zapis sinusa, cosinusa, tangensa i cotangensa - odpowiednio sin, cos, tg i ctg.

Na przykład, jeśli ABC jest trójkątem prostokątnym o kącie prostym C, to sinus kąta ostrego A jest równy stosunkowi przeciwprostokątnej BC do przeciwprostokątnej AB, czyli sin∠A=BC/AB.

Definicje te pozwalają obliczyć wartości sinusa, cosinusa, tangensa i cotangensa kąta ostrego ze znanych długości boków trójkąta prostokątnego, a także ze znanych wartości sinusa, cosinusa, styczna, cotangens i długość jednego z boków, znajdź długości pozostałych boków. Na przykład, gdybyśmy wiedzieli, że w trójkącie prostokątnym ramię AC ma wartość 3, a przeciwprostokątna AB ma wartość 7 , to moglibyśmy obliczyć cosinus kąta ostrego A z definicji: cos∠A=AC/AB=3/7 .

Kąt obrotu

W trygonometrii zaczynają szerzej patrzeć na kąt - wprowadzają pojęcie kąta obrotu. Kąt obrotu, w przeciwieństwie do kąta ostrego, nie ogranicza się do ramek od 0 do 90 stopni, kąt obrotu w stopniach (i radianach) można wyrazić dowolną liczbą rzeczywistą od −∞ do +∞.

W tym świetle definicje sinusa, cosinusa, tangensa i cotangensa nie są już kątem ostrym, ale kątem o dowolnej wielkości - kątem obrotu. Podaje się je poprzez współrzędne x i y punktu A 1 , do którego przechodzi tzw. punkt początkowy A(1, 0) po obrocie o kąt α wokół punktu O - początek prostokątnego układu współrzędnych kartezjańskich i środek okręgu jednostkowego.

Definicja.

Sinus kąta obrotuα jest rzędną punktu A 1 , czyli sinα=y .

Definicja.

cosinus kąta obrotuα nazywamy odciętą punktu A 1 , czyli cosα=x .

Definicja.

Tangens kąta obrotuα jest stosunkiem rzędnej punktu A 1 do jego odciętej, czyli tgα=y/x .

Definicja.

Cotangens kąta obrotuα jest stosunkiem odciętej punktu A 1 do jego rzędnej, czyli ctgα=x/y .

Sinus i cosinus są zdefiniowane dla dowolnego kąta α , ponieważ zawsze możemy wyznaczyć odciętą i rzędną punktu, którą uzyskujemy obracając punkt początkowy o kąt α . A tangens i cotangens nie są zdefiniowane dla żadnego kąta. Styczna nie jest określona dla takich kątów α, przy których punkt początkowy przechodzi do punktu z zerową odciętą (0, 1) lub (0, −1) , a odbywa się to pod kątami 90°+180° k , k∈Z (π /2+π k rad). Rzeczywiście, przy takich kątach obrotu wyrażenie tgα=y/x nie ma sensu, ponieważ zawiera dzielenie przez zero. Jeśli chodzi o cotangens, to nie jest ona zdefiniowana dla takich kątów α, przy których punkt początkowy przechodzi do punktu o zerowej rzędnej (1, 0) lub (−1, 0) , a tak jest w przypadku kątów 180° k , k ∈Z (π k rad).

Tak więc sinus i cosinus są zdefiniowane dla dowolnych kątów obrotu, tangens jest zdefiniowany dla wszystkich kątów z wyjątkiem 90°+180° k , k∈Z (π/2+π k rad), a cotangens jest dla wszystkich kątów z wyjątkiem 180 ° ·k, k∈Z (π·k rad).

Znane nam już notacje pojawiają się w definicjach sin, cos, tg i ctg, są one również używane do oznaczenia sinusa, cosinusa, tangensa i cotangensa kąta obrotu (czasami można spotkać zapisy tan i cot odpowiadające tangens i cotangens). Czyli sinus kąta obrotu 30 stopni można zapisać jako sin30°, zapisy tg(−24°17′) i ctgα odpowiadają tangensowi kąta obrotu −24 stopnie 17 minut i cotangensowi kąta obrotu α . Przypomnijmy, że przy zapisywaniu miary kąta w radianach często pomija się zapis „rad”. Na przykład cosinus kąta obrotu trzech radów jest zwykle oznaczany jako cos3 π .

Na zakończenie tego paragrafu warto zauważyć, że mówiąc o sinusie, cosinusie, tangensie i cotangensie kąta obrotu często pomija się sformułowanie „kąt obrotu” lub słowo „obrót”. Oznacza to, że zamiast wyrażenia „sinus kąta obrotu alfa” zwykle używa się wyrażenia „sinus kąta alfa”, lub nawet krócej - „sinus alfa”. To samo dotyczy cosinusa, tangensa i cotangensa.

Powiedzmy również, że definicje sinusa, cosinusa, tangensa i cotangensa kąta ostrego w trójkącie prostokątnym są zgodne z definicjami właśnie podanymi dla sinusa, cosinusa, tangensa i cotangensa kąta obrotu w zakresie od 0 do 90 stopni. Udowodnimy to.

Liczby

Definicja.

Sinus, cosinus, tangens i cotangens liczby t jest liczbą równą odpowiednio sinusowi, cosinusowi, tangensowi i cotangensowi kąta obrotu w t radianach.

Na przykład, cosinus 8 π jest z definicji liczbą równą cosinusowi kąta 8 π rad. A cosinus kąta w 8 π rad jest równy jeden, więc cosinus liczby 8 π jest równy 1.

Istnieje inne podejście do definicji sinusa, cosinusa, tangensa i cotangensa liczby. Polega ona na tym, że każdej liczbie rzeczywistej t przyporządkowany jest punkt okręgu jednostkowego, którego środek znajduje się w początku układu współrzędnych prostokątnych, a sinus, cosinus, tangens i cotangens są wyznaczane przez współrzędne tego punktu. Zastanówmy się nad tym bardziej szczegółowo.

Pokażmy, jak ustala się zgodność między liczbami rzeczywistymi a punktami koła:

• numer 0 jest przypisany do punktu początkowego A(1, 0) ;
• liczba dodatnia t jest związana z punktem na okręgu jednostkowym, do którego dojdziemy, jeśli okrążymy okrąg od punktu początkowego w kierunku przeciwnym do ruchu wskazówek zegara i przejdziemy drogę o długości t;
• liczba ujemna t jest powiązana z punktem na okręgu jednostkowym, do którego dojdziemy, jeśli okrążymy okrąg od punktu początkowego w kierunku zgodnym z ruchem wskazówek zegara i przejdziemy ścieżką o długości |t| .

Przejdźmy teraz do definicji sinusa, cosinusa, tangensa i cotangensa liczby t. Załóżmy, że liczba t odpowiada punktowi okręgu A 1 (x, y) (na przykład liczba &pi/2; odpowiada punktowi A 1 (0, 1) ).

Definicja.

Sinus liczby t jest rzędną punktu okręgu jednostkowego odpowiadającego liczbie t , czyli sint=y .

Definicja.

Cosinus liczby t nazywamy odciętą punktu okręgu jednostkowego odpowiadającego liczbie t , czyli cost=x .

Definicja.

Tangens liczby t jest stosunkiem rzędnej do odciętej punktu okręgu jednostkowego odpowiadającego liczbie t, czyli tgt=y/x. W innym równoważnym sformułowaniu tangens liczby t jest stosunkiem sinusa tej liczby do cosinusa, to znaczy tgt=sint/cost.

Definicja.

Cotangens liczby t jest stosunkiem odciętej do rzędnej punktu okręgu jednostkowego odpowiadającego liczbie t, czyli ctgt=x/y. Inne sformułowanie jest następujące: tangens liczby t jest stosunkiem cosinusa liczby t do sinusa liczby t : ctgt=cost/sint .

Tutaj zauważamy, że podane właśnie definicje zgadzają się z definicją podaną na początku tego podrozdziału. Rzeczywiście, punkt okręgu jednostkowego odpowiadający liczbie t pokrywa się z punktem uzyskanym przez obrócenie punktu początkowego o kąt t radianów.

Warto też doprecyzować ten punkt. Powiedzmy, że mamy wpis sin3. Jak zrozumieć, czy chodzi o sinus liczby 3 czy sinus kąta obrotu 3 radianów? Zwykle wynika to z kontekstu, w przeciwnym razie prawdopodobnie nie ma to znaczenia.

Funkcje trygonometryczne argumentu kątowego i liczbowego

Zgodnie z definicjami podanymi w poprzednim akapicie, każdy kąt obrotu α odpowiada ściśle określonej wartości sinα, jak również wartości cosα. Ponadto wszystkie kąty obrotu inne niż 90°+180° k , k∈Z (π/2+π k rad) odpowiadają wartościom tgα , a inne niż 180° k , k∈Z (π k rad ) są wartościami ctgα . Zatem sinα, cosα, tgα i ctgα są funkcjami kąta α. Innymi słowy, są to funkcje argumentu kątowego.

Podobnie możemy mówić o funkcjach sinus, cosinus, tangens i cotangens argumentu liczbowego. Rzeczywiście, każda liczba rzeczywista t odpowiada ściśle określonej wartości sint , a także kosztu . Ponadto wszystkie liczby inne niż π/2+π·k , k∈Z odpowiadają wartościom tgt , a liczby π·k , k∈Z odpowiadają wartościom ctgt .

Funkcje sinus, cosinus, tangens i cotangens są nazywane podstawowe funkcje trygonometryczne.

Z kontekstu zwykle wynika, że ​​mamy do czynienia z funkcjami trygonometrycznymi argumentu kątowego lub liczbowego. W przeciwnym razie możemy uznać zmienną niezależną zarówno za miarę kąta (argument kąta), jak i za argument liczbowy.

Jednak szkoła zajmuje się głównie funkcjami liczbowymi, czyli funkcjami, których argumentami, a także odpowiadającymi im wartościami funkcji, są liczby. Dlatego, jeśli mówimy o funkcjach, to warto rozważyć funkcje trygonometryczne jako funkcje argumentów liczbowych.

Połączenie definicji z geometrii i trygonometrii

Jeżeli weźmiemy pod uwagę kąt obrotu α od 0 do 90 stopni, to dane w kontekście trygonometrii definicji sinusa, cosinusa, tangensa i cotangensa kąta obrotu są w pełni zgodne z definicjami sinusa, cosinusa , tangens i cotangens kąta ostrego w trójkącie prostokątnym, które są podane w kursie geometrii. Udowodnijmy to.

Narysuj okrąg jednostkowy w prostokątnym kartezjańskim układzie współrzędnych Oxy. Zwróć uwagę na punkt początkowy A(1, 0) . Obróćmy go o kąt α w zakresie od 0 do 90 stopni, otrzymujemy punkt A 1 (x, y) . Spuśćmy prostopadłą A 1 H z punktu A 1 do osi Ox.

Łatwo zauważyć, że w trójkącie prostokątnym kąt A 1 OH jest równy kątowi obrotu α, długość ramienia OH sąsiadującego z tym kątem jest równa odciętej punktu A 1, czyli |OH |=x, długość ramienia A 1 H przeciwna do kąta jest równa rzędnej punktu A 1 , czyli |A 1 H|=y , a długość przeciwprostokątnej OA 1 jest równa jeden , ponieważ jest to promień okręgu jednostkowego. Wtedy, z definicji z geometrii, sinus kąta ostrego α w trójkącie prostokątnym A 1 OH jest równy stosunkowi odnogi przeciwnej do przeciwprostokątnej, czyli sinα=|A 1 H|/|OA 1 |= y/1=y . A z definicji z trygonometrii sinus kąta obrotu α jest równy rzędnej punktu A 1, czyli sinα=y. To pokazuje, że definicja sinusa kąta ostrego w trójkącie prostokątnym jest równoważna definicji sinusa kąta obrotu α dla α od 0 do 90 stopni.

Podobnie można wykazać, że definicje cosinusa, tangensa i cotangensa kąta ostrego α są zgodne z definicjami cosinusa, tangensa i cotangensa kąta obrotu α.

Bibliografia.

1. Geometria. 7-9 klas: studia. dla kształcenia ogólnego instytucje / [L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev i inni]. - 20. ed. M.: Edukacja, 2010. - 384 s.: chor. - ISBN 978-5-09-023915-8.
2. Pogorełow A.V. Geometria: proc. na 7-9 komórek. ogólne wykształcenie instytucje / A. V. Pogorelov. - wyd. 2 - M.: Oświecenie, 2001. - 224 s.: il. - ISBN 5-09-08083-X.
3. Algebra i funkcje elementarne: Podręcznik dla uczniów klasy 9 szkoły średniej / E. S. Kochetkov, E. S. Kochetkova; Pod redakcją doktora nauk fizycznych i matematycznych O. N. Golovina - wyd. Moskwa: Edukacja, 1969.
4. Algebra: Proc. na 9 komórek. śr. szkoła / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Wyd. S. A. Telyakovsky.- M.: Oświecenie, 1990.- 272 s.: Ill.- ISBN 5-09-002727-7
5. Algebra i początek analizy: Proc. na 10-11 komórek. ogólne wykształcenie instytucje / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn i inni; Wyd. A. N. Kolmogorova.- 14. wyd.- M.: Oświecenie, 2004.- 384 s.: il.- ISBN 5-09-013651-3.
6. Mordkovich AG Algebra i początki analizy. Klasa 10. 14.00 Część 1: podręcznik dla instytucji edukacyjnych (poziom profilu) / A.G. Mordkovich, P.V. Semenov. - wyd. 4, dodaj. - M.: Mnemosyne, 2007. - 424 s.: ch. ISBN 978-5-346-00792-0.
7. Algebra i początek analizy matematycznej. Klasa 10: podręcznik. dla kształcenia ogólnego instytucje: podstawowe i profilowe. poziomy /[Ju. M. Kolagin, M.V. Tkacheva, N.E. Fedorova, M.I. Shabunin]; wyd. A. B. Zhizhchenko. - 3. ed. - I.: Edukacja, 2010. - 368 s.: III. - ISBN 978-5-09-022771-1.
8. Bashmakov MI Algebra i początek analizy: Proc. na 10-11 komórek. śr. Szkoła - 3. ed. - M.: Oświecenie, 1993. - 351 s.: ch. - ISBN 5-09-004617-4.
9. Gusiew V.A., Mordkovich A.G. Matematyka (podręcznik dla kandydatów do szkół technicznych): Proc. dodatek.- M.; Wyższy szkoła, 1984.-351 s., chor.

Z wykresów widać, że:

1. Wykresy sinus i cosinus wahają się od -1 do 1
2. Krzywa cosinus ma taki sam kształt jak krzywa sinus, ale jest przesunięta względem niej o 90 stopni
3. Krzywe sinus i cosinus są ciągłe i powtarzają się z okresem 360 o , krzywa styczna ma nieciągłości i powtarza się z okresem 180 o .

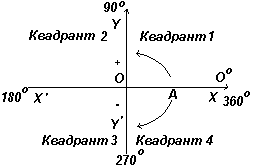Na ryc. po lewej stronie pokazane są prostopadłe osie XX" i YY"; przecinające się w początku O. Podczas pracy z wykresami pomiary w prawo i w górę od O są uważane za dodatnie, w lewo i w dół od O - ujemne. Niech OA obraca się swobodnie względem O. Kiedy OA jest obracany w kierunku przeciwnym do ruchu wskazówek zegara, zmierzony kąt jest uważany za dodatni, a gdy jest obracany zgodnie z ruchem wskazówek zegara, jest ujemny.

Harmonogram. pozytywny lub negatywny
kierunek w ruchu kołowym.

Niech OA obraca się w kierunku przeciwnym do ruchu wskazówek zegara w taki sposób, że Θ 1 jest dowolnym kątem w pierwszej ćwiartce i skonstruuj prostopadły AB, aby otrzymać prostokąt prostokątny OAB na ryc. lewy. Ponieważ wszystkie trzy boki trójkąta są dodatnie, funkcje trygonometryczne sinus, cosinus i tangens w pierwszej ćwiartce będą dodatnie. (Zauważ, że długość OA jest zawsze dodatnia, ponieważ jest to promień okręgu.)
Niech OA obraca się dalej w taki sposób, że Θ 2 jest dowolnym kątem w drugiej ćwiartce i skonstruuj AC tak, aby powstał trójkąt prostokątny OAC. Wtedy grzech Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Niech OA obraca się dalej w taki sposób, że Θ 3 jest dowolnym kątem w trzecim kwadrancie i skonstruuj AD tak, aby powstał trójkąt prostokątny OAD. Wtedy grzech Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

Harmonogram. Kąty budowlane w
różne ćwiartki.

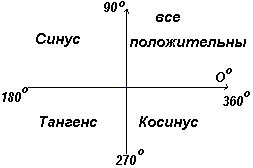Niech OA obraca się dalej w taki sposób, że Θ 4 jest dowolnym kątem w czwartym kwadrancie i skonstruuj AE tak, aby powstał prostokątny OAE. Wtedy grzech Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

W pierwszym kwadrancie wszystkie funkcje trygonometryczne mają wartości dodatnie, w drugim tylko sinus, w trzecim tylko tangens, w czwartym tylko cosinus, co pokazano na rys. lewy.

Znajomość kątów o dowolnej wielkości jest niezbędna przy znajdowaniu, na przykład, wszystkich kątów między 0o a 360o, których sinus wynosi powiedzmy 0,3261. Jeśli wpiszesz do kalkulatora 0.3261 i wciśniesz przycisk sin -1, otrzymamy odpowiedź 19.03 o. Istnieje jednak drugi kąt pomiędzy 0 o a 360 o, którego kalkulator nie pokaże. Sinus jest dodatni również w drugiej ćwiartce. Drugi kąt pokazano na ryc. poniżej jako kąt Θ, gdzie Θ=180 o - 19,03 o = 160,97 o . Zatem 19,03o i 160,97o to kąty z zakresu od 0o do 360o, których sinus wynosi 0,3261.

Bądź ostrożny! Kalkulator podaje tylko jedną z tych wartości. Drugą wartość należy wyznaczyć zgodnie z teorią kątów o dowolnej wielkości.

Przykład 1

Znajdź wszystkie kąty pomiędzy 0 o a 360 o, których sinus wynosi -0,7071

Rozwiązanie:
Kąty, których sinus wynosi -0,7071 o są w trzeciej i czwartej ćwiartce, ponieważ sinus jest ujemny w tych ćwiartkach (patrz rysunek po lewej).

Harmonogram. Znajdowanie wszystkich kątów według
podana wartość sinus (przykład)

Z poniższego rysunku Θ = arcsin 0,7071 = 45 o . Dwa kąty w zakresie od 0 o do 360 o, których sinus wynosi -0,7071, wynoszą 180 o +45 o \u003d 225 o i 360 o - 45 o \u003d 315 o.

Notatka. Kalkulator daje tylko jedną odpowiedź.
Harmonogram. Znajdowanie wszystkich kątów według
podana wartość sinus (przykład)

Przykład 2

Znajdź wszystkie kąty z zakresu od 0 o do 360 o, których styczna wynosi 1,327.

Rozwiązanie:
Styczna jest dodatnia w pierwszej i trzeciej ćwiartce - ryc. lewy.
Harmonogram. Znajdowanie wszystkich kątów według

Z poniższego rysunku Θ = arctan1,327= 53 o .
Dwa kąty z zakresu od 0o do 360o, których styczna wynosi 1,327 to 53o i 180o+53o, tj. 233o.
Harmonogram. Znajdowanie wszystkich kątów według
podana wartość stycznej (przykład)

Niech OR na ryc. po lewej stronie jest wektor długości jednostkowej, obracający się swobodnie w kierunku przeciwnym do ruchu wskazówek zegara wokół O. Jeden obrót tworzy okrąg pokazany na ryc. i podzielone przez sektory 15 o . Każdy promień ma składową poziomą i pionową. Na przykład dla 30 o składnik pionowy to TS, a składnik poziomy to OS.

Z definicji funkcji trygonometrycznych
sin30 o =TS/TO=TS/1, czyli TS=sin30o I cos30o=OS/TO=OS/1, tj. OS=cos30o

Składowa pionowa TS może być wykreślona jako T"S", która jest równa wartości odpowiadającej kątowi 30° na wykresie y względem kąta x. Jeśli wszystkie składowe pionowe, takie jak TS, zostaną przeniesione na wykres, otrzymamy sinusoidę, pokazaną na ryc. nad.

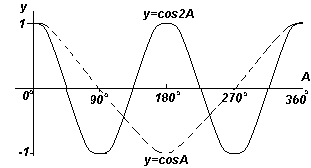
Jeśli wszystkie składowe poziome, takie jak OS, są rzutowane na wykres y vs. x, otrzymujemy falę cosinus. Te rzuty są łatwe do wizualizacji poprzez przerysowanie okręgu o promieniu OR i kątach wychodzących od pionu, jak pokazano na rysunku po lewej stronie.
Z ryc. po lewej stronie widać, że sinusoida ma taki sam kształt jak fala cosinus, ale przesunięta o 90 o .

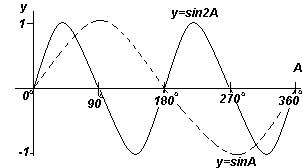Funkcje okresowe i okres
Każdy z wykresów funkcji pokazanych na czterech ryc. powyżej, powtarza się wraz ze wzrostem kąta A, więc nazywa się je funkcje okresowe.
Funkcje y=sinA i y=cosA są powtarzane co 360 o (lub 2π radianów), więc 360 o nazywa się Kropka te funkcje. Funkcje y=sin2A i y=cos2A powtarzają się co 180 o (lub π radianów), więc 180 o jest okresem dla tych funkcji.
Ogólnie, jeśli y=sinpA i y=cospA (gdzie p jest stałą), to okres funkcji wynosi 360 o /p (lub 2π/p radianów). Zatem jeśli y=sin3A to okres tej funkcji wynosi 360o/3=120o, jeśli y=cos4A to okres tej funkcji wynosi 360o/4=90o.

Amplituda
Amplituda nazywana maksymalną wartością sinusoidy. Każdy z wykresów 1-4 ma amplitudę +1 (tj. wahają się od +1 do -1). Jeśli jednak y=4sinA, każda z wartości sinA jest mnożona przez 4, więc maksymalna wartość amplitudy wynosi 4. Podobnie dla y=5cos2A amplituda wynosi 5, a okres 360o/2=180o.

Przykład 3
Zbuduj y=3sin2A w zakresie od A=0o do A=360o.

Rozwiązanie:
Amplituda =3, okres = 360o/2 =180o.

Przykład 4
Wykres y=4cos2x w zakresie od x=0o do x=360o

Rozwiązanie:
Amplituda = 4. okres = 360 o /2 = 180 o .

Kąty opóźnienia i wyprzedzenia
Krzywe sinus i cosinus nie zawsze zaczynają się od 0 o . Aby uwzględnić tę okoliczność, funkcję okresową przedstawia się jako y=sin(A± α), gdzie α jest przesunięciem fazowym względem y=sinA i y=cosA.

Po skompilowaniu tabeli wartości można wykreślić funkcję y=sin(A-60 o), pokazaną na ryc. lewy. Jeżeli krzywa y=sinA zaczyna się od 0o, to krzywa y=sin(A-60o) zaczyna się od 60o (czyli jej wartość zero wynosi 60o w prawo). Mówi się więc, że y=sin(A-60 o) późno względem y=sinA o 60°.
Harmonogram. y=sin(A-60 o) (sinusoida).

Po skompilowaniu tabeli wartości można wykreślić funkcję y=cos(A+45o), pokazaną na ryc. poniżej.
Jeżeli krzywa y=cosA zaczyna się w 0o, to krzywa y=cos(A+45o) zaczyna się o 45o w lewo (tzn. jej wartość zero wynosi 45o wcześniej).
Tak więc mówi się, że wykres ma postać y=cos(A+45o) przed wykres y=cosA przy 45°.
Harmonogram. y=cos(A+45o) (cosinus).

Ogólnie rzecz biorąc, wykres y=sin(A-α) jest opóźniony względem y=sinA o kąt α.
Fala cosinusoidalna ma taki sam kształt jak sinusoida, ale zaczyna się pod kątem 90 o w lewo, tj. wyprzedza ją o 90 o . Zatem cosA=sin(A+90o).

Przykład 5
Wykres y=5sin(A+30o) w zakresie od A=0o do A=360o

Rozwiązanie:
Amplituda = 5, okres = 360 o /1 = 360 o .
5sin(A+30o) wyprzedza 5sinA o 30o tj. zaczyna się 30 o wcześniej.
Wykres y=5sin(A+30o) (sinusoida).

Przykład 6
Wykres y=7sin(2A-π/3) w zakresie od A=0o do A=360o.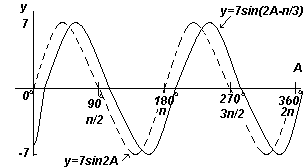

Rozwiązanie:
Amplituda = 7, okres = 2π/2= π radiany
Ogólnie y=sin(pt-α) opóźnienia względem y=sinpt o α/p, zatem 7sin(2A-π/3) jest opóźniony względem 7sin2A o (π/3)/2, tj. na π/6 radianów lub 30 o

Sinusoida postaci Asin(ωt±α). kąt fazowy. Przesunięcie fazowe.

Niech OR na ryc. po lewej wektor swobodnie obracający się w kierunku przeciwnym do ruchu wskazówek zegara wokół O z prędkością ω radianów/s. Wektor obracający się nazywa się wektor fazowy. Po czasie t sekund OR obróci się o kąt ωt w radianach (na rysunku po lewej jest to kąt TOR). Jeśli ST jest zbudowane prostopadle do OR, to sinωt=ST/OT, tj. ST=OTsinωt.
Jeśli wszystkie takie składowe pionowe zostaną zrzutowane na wykres y w funkcji ωt, otrzymamy sinusoidę o amplitudzie OR.

Jeżeli wektor fazowy OR wykonuje jeden obrót (tj. 2π radianów) w T sekund, to prędkość kątowa ω=2π/T rad/s, skąd
Т=2π/ ω (s), gdzie
T jest Kropka
Liczba pełnych okresów, które mijają w ciągu 1 sekundy, nazywa się częstotliwość F.
Częstotliwość = (liczba okresów)/(sekunda) = 1/ T = ω/2π Hz, tych. f= ω/2π Hz
Dlatego prędkość kątowa
ω=2πf rad/s.

Jeśli ogólnie funkcja sinusoidalna wygląda tak: y=sin(ωt± α), to
A - amplituda
ω - prędkość kątowa
2π/ ω - okres T, s
ω/2π - częstotliwość f, Hz
α jest kątem wyprzedzenia lub opóźnienia (w stosunku do y=Аsinωt) w radianach, nazywany jest również kątem fazowym.

Przykład 7
Prąd przemienny podawany jest jako i=20sin(90πt+0,26) amperów. Określ amplitudę, okres, częstotliwość i kąt fazowy (w stopniach)

Rozwiązanie:
i \u003d 20sin (90πt + 0,26) A zatem
amplituda jest 20 lat
prędkość kątowa ω=90π, zatem
koniec dyskusji= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
częstotliwość F\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
kąt fazowy α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.

Przykład 8
Mechanizm oscylacyjny ma maksymalne przemieszczenie 3 mi częstotliwość 55 Hz. W czasie t=0 przemieszczenie wynosi 100 cm. Wyraź przesunięcie w postaci ogólnej Аsin(ωt± α).

Rozwiązanie
Amplituda = maksymalna przemieszczenie = 3m
Prędkość kątowa ω=2πf = 2π(55) = 110 rad/s
Dlatego przemieszczenie wynosi 3sin(110πt + α)m.
Przy przesunięciu t=0 = 100cm=1m.
Dlatego 1= 3sin(0 + α), tj. sinα=1/3=0,33
Zatem α=arcsin0,33=19 o
Zatem przesunięcie wynosi 3sin(110 πt + 0,33).

Przykład 9
Wartość chwilowego napięcia w obwodzie prądu przemiennego w dowolnej t sekund jest podawana jako v=350sin(40πt-0,542)V. Znaleźć:
a) Amplituda, okres, częstotliwość i kąt fazowy (w stopniach)
b) wartość napięcia w t = 0
c) wartość napięcia przy t = 10 ms
d) czas potrzebny do osiągnięcia napięcia 200 V po raz pierwszy.
Rozwiązanie:
a) Amplituda 350 V, prędkość kątowa ω=40π
W konsekwencji,
okres Т=2π/ ω=2π/40π=0,05 s =50ms
częstotliwość f=1/T=1/0,05=20 Hz
kąt fazowy \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o z opóźnieniem względem v \u003d 350sin (40πt)
b) Jeśli t \u003d 0, to v \u003d 350 sin (0-0,542) \u003d 350 sin (-31 o) \u003d -180,25 V
c) Jeśli t \u003d 10 ms, to v \u003d 350 sin (40π10 / 10 3 -0,542) \u003d 350 sin (0,714) \u003d 350 sin41 o \u003d 229,6 V
d) Jeśli v=200 AND, to 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

Harmonogram. Mechanizm oscylacyjny
(przykład sinusoida).

v=350sin(40πt-0,542) Zatem (40πt-0,542)=arcsin200/350=35o lub 0,611 rad.
40πt= 0,611+0,542=1,153.
Zatem jeśli v=200V, to czas t=1,153/40π=9,179 ms

Geometryczna definicja sinusa i cosinusa

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α to kąt wyrażony w radianach.

Zatoka jest funkcją trygonometryczną kąta α między przeciwprostokątną a odnogą trójkąta prostokątnego, równą stosunkowi długości przeciwprostokątnej |BC| do długości przeciwprostokątnej |AB|.

Cosinus (cos α) jest funkcją trygonometryczną kąta α między przeciwprostokątną a ramieniem trójkąta prostokątnego, równą stosunkowi długości sąsiedniego ramienia |AC| do długości przeciwprostokątnej |AB|.

Definicja trygonometryczna

Korzystając z powyższych wzorów, możesz znaleźć sinus i cosinus kąta ostrego. Ale musisz nauczyć się obliczać sinus i cosinus kąta o dowolnej wielkości. Trójkąt prostokątny nie daje takiej możliwości (na przykład kąt rozwarty nie może się w nim znajdować); dlatego potrzebna jest bardziej ogólna definicja sinusa i cosinusa, zawierająca te formuły jako przypadek szczególny.

Z pomocą przychodzi krąg trygonometryczny. Niech będzie dany kąt; odpowiada punktowi o tej samej nazwie na okręgu trygonometrycznym.

Ryż. 2. Definicja trygonometryczna sinusa i cosinusa

Cosinus kąta to odcięta punktu. Sinus kąta jest rzędną punktu.

Na ryc. 2 kąt jest traktowany jako ostry i łatwo zrozumieć, że definicja ta pokrywa się z ogólną definicją geometryczną. Rzeczywiście, widzimy trójkąt prostokątny z jednostkową przeciwprostokątną O i kątem ostrym. Sąsiedni odcinek tego trójkąta to cos (porównaj z ryc. 1) i jednocześnie odcięta punktu; przeciwna noga to grzech (jak na ryc. 1) i jednocześnie rzędna punktu.

Ale teraz nie jesteśmy już ograniczeni pierwszym kwartałem i mamy możliwość rozszerzenia tej definicji pod dowolnym kątem. Na ryc. 3 pokazuje, jaki jest sinus i cosinus kąta w drugiej, trzeciej i czwartej ćwiartce.

Ryż. 3. Sinus i cosinus w ćwiartce II, III i IV

Tabela wartości sinusa i cosinusa

Kąt zerowy \(\LARGE 0^(\circ ) \)

Odcięta punktu 0 to 1 , rzędna punktu 0 to 0 . W konsekwencji,

cos 0 = 1 sin 0 = 0

Rys 4. Kąt zerowy

Kąt \(\LARGE \frac(\pi)(6) = 30^(\circ ) \)

Widzimy trójkąt prostokątny z jednostkową przeciwprostokątną i kątem ostrym 30°. Jak wiecie, noga przeciwna do kąta 30 ° jest równa połowie przeciwprostokątnej 1; innymi słowy, pionowa noga jest równa 1/2, a zatem

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Odnogę poziomą znajdujemy za pomocą twierdzenia Pitagorasa (lub, co jest identyczne, znajdujemy cosinus zgodnie z podstawową tożsamością trygonometryczną):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 Dlaczego tak się dzieje? Wytnij trójkąt równoboczny o boku 2 wzdłuż jego wysokości! Dzieli się na dwa trójkąty prostokątne z przeciwprostokątną 2, kątem ostrym 30° i mniejszą odnogą 1.

Rys 5. Kąt π / 6

Kąt \(\LARGE \frac(\pi)(4) = 45^(\circ ) \)

W tym przypadku prawy trójkąt to równoramienny; sinus i cosinus kąta 45° są sobie równe. Oznaczmy je na razie przez x. Mamy:

\[ x^(2) + x^(2) = 1 \]

skąd \(x=\frac(\sqrt(2) )(2) \). W konsekwencji,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Rys 5. Kąt π / 4

Własności sinusa i cosinusa

Przyjęte oznaczenia

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Okresowość

Funkcje y = sin x i y = cos x są okresowe z okresem 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Parytet

Funkcja sinus jest nieparzysta. Funkcja cosinus jest parzysta.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Domeny definicji i wartości, ekstrema, wzrost, spadek

Główne właściwości sinusa i cosinusa przedstawiono w tabeli ( n- liczba całkowita).

	\(\mały< x < \)	\(\mały -\pi + 2\pi n \) \(\mały< x < \) \(\small 2\pi n \)
Malejąco	\(\mały \dfrac(\pi)2 + 2\pi n \)\(\mały< x < \) \(\mały \dfrac(3\pi)2 + 2\pi n \)	\(\mały 2\pi n \) \(\mały< x < \) \(\pi + \small 2\pi n \)
Maksimum, \(\mały x = \) \(\mały \dfrac(\pi)2 + 2\pi n \)	\(\mały x = 2\pi n \)
Minima, \(\mały x = \) \(\small -\dfrac(\pi)2 + 2\pi n \)	\(\mały x = \) \(\mały \pi + 2\pi n \)
Zera, \(\mały x = \pi n \)	\(\mały x = \dfrac(\pi)2 + \pi n \)
Punkty przecięcia z osią y, x = 0	y=0	y=1

Podstawowe formuły zawierające sinus i cosinus

Suma kwadratów

\(\sin^2 x + \cos^2 x = 1 \)

Wzory na sumę i różnicę sinus i cosinus

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Wzory na iloczyn sinusów i cosinusów

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)

Wzory na sumy i różnice

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Wyrażenie od sinusa do cosinusa

\(\sin x = \cos\lewo(\dfrac(\pi)2 - x \prawo) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Wyrażanie cosinusa przez sinus

\(\cos x = \sin\lewo(\dfrac(\pi)2 - x \prawo) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Wyrażenie w kategoriach stycznych

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

Na \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

Na \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Tablica sinusów i cosinusów, tangensów i cotangensów

Ta tabela pokazuje wartości sinusów i cosinusów dla niektórych wartości argumentu.
[ img style="maks.-szerokość:500px;maks.-wysokość:1080px;" src="tablitsa.png" alt="(!LANG: Tablica sinusów i cosinusów" title="Tabela sinusów i cosinusów" ]!}

Wyrażenia poprzez złożone zmienne

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Wzór Eulera

\(e^(iz) = \cos z + i \sin z \)

Wyrażenia w kategoriach funkcji hiperbolicznych

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Pochodne

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Wyprowadzanie wzorów > > >

Pochodne n-tego rzędu:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Całki

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Zobacz także rozdział Tabela całek nieoznaczonych >>>

Rozszerzenia w serie

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Secans, cosecans

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

Funkcje odwrotne

Funkcje odwrotne do sinusa i cosinusa to odpowiednio arcsine i arccosinus.

Arcsine, arcsin

\(y = \arcsin x \) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

Arccosinus, arccos

\(y = \arccos x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Bibliografia:
W. Bronstein, K.A. Semendyaev, Podręcznik matematyki dla inżynierów i studentów wyższych uczelni, Lan, 2009.

Javascript jest wyłączony w Twojej przeglądarce.
Kontrolki ActiveX muszą być włączone, aby móc wykonywać obliczenia!

Wyśrodkowany w punkcie A .
α to kąt wyrażony w radianach.

Styczna ( tgα) jest funkcją trygonometryczną zależną od kąta α między przeciwprostokątną a odnogą trójkąta prostokątnego, równą stosunkowi długości przeciwprostokątnej |BC| do długości sąsiedniej nogi |AB| .

Cotangens ( ctgα) jest funkcją trygonometryczną zależną od kąta α między przeciwprostokątną a odnogą trójkąta prostokątnego, równą stosunkowi długości sąsiedniego ramienia |AB| do długości przeciwległej nogi |BC| .

Tangens

Gdzie n- cały.

W literaturze zachodniej tangens oznaczany jest następująco:
.
;
;
.

Wykres funkcji stycznej, y = tg x

Cotangens

Gdzie n- cały.

W literaturze zachodniej cotangens oznacza się następująco:
.
Przyjęto również następującą notację:
;
;
.

Wykres funkcji cotangens, y = ctg x

Własności tangensa i cotangensa

Okresowość

Funkcje y= tg x i y= ctg x są okresowe z okresem π.

Parytet

Funkcje tangens i cotangens są nieparzyste.

Domeny definicji i wartości, rosnąco, malejąco

Funkcje tangens i cotangens są ciągłe w swojej dziedzinie definicji (patrz dowód ciągłości). Główne właściwości stycznej i cotangensa przedstawiono w tabeli ( n- liczba całkowita).

	y= tg x	y= ctg x
Zakres i ciągłość
Zakres wartości	-∞ < y < +∞	-∞ < y < +∞
Rosnąco		-
Malejąco	-
Ekstrema	-	-
Zera, y= 0
Punkty przecięcia z osią y, x = 0	y= 0	-

Formuły

Wyrażenia w postaci sinusa i cosinusa

; ;
; ;
;

Wzory na tangens i cotangens sumy i różnicy

Reszta formuł jest łatwa do zdobycia, na przykład

Iloczyn stycznych

Wzór na sumę i różnicę stycznych

Ta tabela pokazuje wartości tangensów i cotangensów dla niektórych wartości argumentu.

Wyrażenia w postaci liczb zespolonych

Wyrażenia w kategoriach funkcji hiperbolicznych

;
;

Pochodne

; .

.
Pochodna n-tego rzędu względem zmiennej x funkcji :
.
Wyprowadzenie wzorów na styczną > > > ; dla cotangensa > > >

Całki

Rozszerzenia w serie

Aby uzyskać rozwinięcie tangensa w potęgach x, musisz wziąć kilka wyrazów rozwinięcia w szereg potęgowy dla funkcji grzech x I bo x i podziel te wielomiany na siebie , . Daje to następujące formuły.

Na .

w .
gdzie B n- Liczby Bernoulliego. Są one wyznaczane albo z relacji rekurencyjności:
;
;
gdzie .
Lub według formuły Laplace'a:

Funkcje odwrotne

Funkcje odwrotne do tangensa i cotangensa to odpowiednio arcus tangens i arccotangens.

Arcus tangens, arctg

, gdzie n- cały.

Arc tangens, arcctg

, gdzie n- cały.

Bibliografia:
W. Bronstein, K.A. Semendyaev, Podręcznik matematyki dla inżynierów i studentów wyższych uczelni, Lan, 2009.
G. Korn, Handbook of Mathematics for Researchers and Engineers, 2012.

Wyśrodkowany w punkcie A.
α to kąt wyrażony w radianach.

Definicja
Zatoka jest funkcją trygonometryczną zależną od kąta α między przeciwprostokątną a odnogą trójkąta prostokątnego, równą stosunkowi długości przeciwprostokątnej |BC| do długości przeciwprostokątnej |AC|.

Cosinus (cos α) jest funkcją trygonometryczną zależną od kąta α między przeciwprostokątną a odnogą trójkąta prostokątnego, równą stosunkowi długości sąsiedniego ramienia |AB| do długości przeciwprostokątnej |AC|.

Przyjęte oznaczenia

;
;
.

;
;
.

Wykres funkcji sinus, y = sin x

Wykres funkcji cosinus, y = cos x

Własności sinusa i cosinusa

Okresowość

Funkcje y= grzech x i y= bo x okresowy z kropką 2 pi.

Parytet

Funkcja sinus jest nieparzysta. Funkcja cosinus jest parzysta.

Domena definicji i wartości, ekstrema, wzrost, spadek

Funkcje sinus i cosinus są ciągłe w swojej dziedzinie definicji, to znaczy dla wszystkich x (patrz dowód ciągłości). Ich główne właściwości przedstawiono w tabeli (n - liczba całkowita).

	y= grzech x	y= bo x
Zakres i ciągłość	- ∞ < x < + ∞	- ∞ < x < + ∞
Zakres wartości	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Rosnąco
Malejąco
Maksimum, y= 1
Minima, y ​​= - 1
Zera, y= 0
Punkty przecięcia z osią y, x = 0	y= 0	y= 1

Podstawowe formuły

Suma sinusa do kwadratu i cosinusa

Wzory sinus i cosinus na sumę i różnicę

;
;

Wzory na iloczyn sinusów i cosinusów

Wzory na sumy i różnice

Wyrażenie od sinusa do cosinusa

;
;
;
.

Wyrażanie cosinusa przez sinus

;
;
;
.

Wyrażenie w kategoriach stycznych

; .

Dla , mamy:
; .

Na :
; .

Tablica sinusów i cosinusów, tangensów i cotangensów

Ta tabela pokazuje wartości sinusów i cosinusów dla niektórych wartości argumentu.

Wyrażenia poprzez złożone zmienne

;

Wzór Eulera

Wyrażenia w kategoriach funkcji hiperbolicznych

;
;

Pochodne

; . Wyprowadzanie wzorów > > >

Pochodne n-tego rzędu:
{ -∞ < x < +∞ }

Secans, cosecans

Funkcje odwrotne

Funkcje odwrotne do sinusa i cosinusa to odpowiednio arcsine i arccosinus.

Arcsine, arcsin

Arccosinus, arccos

Bibliografia:
W. Bronstein, K.A. Semendyaev, Podręcznik matematyki dla inżynierów i studentów wyższych uczelni, Lan, 2009.