Sinuso ir jo grafiko savybės. Sinuso, kosinuso, liestinės ir kotangento savybės

Šiame straipsnyje mes parodysime, kaip kampo ir skaičiaus sinuso, kosinuso, liestinės ir kotangento apibrėžimai trigonometrijoje. Čia kalbėsime apie žymėjimą, pateiksime įrašų pavyzdžių, pateiksime grafines iliustracijas. Apibendrinant, mes nubrėžiame paralelę tarp sinuso, kosinuso, liestinės ir kotangento apibrėžimų trigonometrijoje ir geometrijoje.

Puslapio naršymas.

Sinuso, kosinuso, liestinės ir kotangento apibrėžimas

Stebėkime, kaip mokykliniame matematikos kurse formuojasi sinuso, kosinuso, liestinės ir kotangento sąvokos. Geometrijos pamokose pateikiamas stačiojo trikampio smailiojo kampo sinuso, kosinuso, liestinės ir kotangento apibrėžimas. O vėliau tiriama trigonometrija, kuri reiškia sukimosi kampo ir skaičiaus sinusą, kosinusą, tangentą ir kotangentą. Pateikiame visus šiuos apibrėžimus, pateikiame pavyzdžių ir pateikiame reikiamas pastabas.

Smailusis kampas stačiakampiame trikampyje

Iš geometrijos eigos žinomi stačiojo trikampio smailiojo kampo sinuso, kosinuso, liestinės ir kotangento apibrėžimai. Jie pateikiami kaip stačiojo trikampio kraštinių santykis. Pateikiame jų formuluotes.

Apibrėžimas.

Stačiojo trikampio smailiojo kampo sinusas yra priešingos kojos ir hipotenuzės santykis.

Apibrėžimas.

Stačiojo trikampio smailiojo kampo kosinusas yra gretimos kojos ir hipotenuzės santykis.

Apibrėžimas.

Stačiojo trikampio smailiojo kampo liestinė yra priešingos kojos ir gretimos kojos santykis.

Apibrėžimas.

Stačiojo trikampio smailiojo kampo kotangentė yra gretimos kojos ir priešingos kojos santykis.

Čia taip pat įvedamas sinuso, kosinuso, liestinės ir kotangento žymėjimas - atitinkamai sin, cos, tg ir ctg.

Pavyzdžiui, jei ABC yra stačiakampis trikampis su stačiu kampu C, tai smailiojo kampo A sinusas yra lygus priešingos kojos BC santykiui su hipotenuze AB, tai yra sin∠A=BC/AB.

Šie apibrėžimai leidžia apskaičiuoti smailaus kampo sinuso, kosinuso, liestinės ir kotangento reikšmes iš žinomų stačiojo trikampio kraštinių ilgių, taip pat iš žinomų sinuso, kosinuso verčių, liestinė, kotangentas ir vienos iš kraštinių ilgis, raskite kitų kraštinių ilgius. Pavyzdžiui, jei žinotume, kad stačiakampiame trikampyje kojos AC yra 3, o hipotenuzė AB yra 7, tai smailiojo kampo A kosinusą galėtume apskaičiuoti pagal apibrėžimą: cos∠A=AC/AB=3/7 .

Sukimosi kampas

Trigonometrijoje jie pradeda žiūrėti į kampą plačiau – įveda sukimosi kampo sąvoką. Sukimosi kampas, skirtingai nuo smailaus kampo, neribojamas rėmeliais nuo 0 iki 90 laipsnių, sukimosi kampas laipsniais (ir radianais) gali būti išreikštas bet kokiu realiu skaičiumi nuo −∞ iki +∞.

Šioje šviesoje sinuso, kosinuso, liestinės ir kotangento apibrėžimai nebėra smailusis kampas, o savavališko dydžio kampas – sukimosi kampas. Jie pateikiami per taško A 1 x ir y koordinates, į kuriuos, pasisukus kampu α aplink tašką O - stačiakampės Dekarto koordinačių sistemos pradžia, patenka vadinamasis pradinis taškas A(1, 0). ir vieneto apskritimo centras.

Apibrėžimas.

Sukimosi kampo sinusasα yra taško A 1 ordinatė, tai yra sinα=y .

Apibrėžimas.

sukimosi kampo kosinusasα vadinama taško A 1 abscise, tai yra cosα=x .

Apibrėžimas.

Sukimosi kampo liestinėα yra taško A 1 ordinatės ir jo abscisių santykis, tai yra, tgα=y/x .

Apibrėžimas.

Sukimosi kampo kotangentasα – taško A 1 abscisių santykis su jo ordinatėmis, tai yra ctgα=x/y .

Sinusas ir kosinusas apibrėžiami bet kuriam kampui α, nes visada galime nustatyti taško abscisę ir ordinatę, kuri gaunama pasukus pradinį tašką kampu α. O tangentas ir kotangentas nėra apibrėžti jokiam kampui. Tokiems kampams α, kuriuose pradinis taškas eina į tašką su nuline abscise (0, 1) arba (0, −1) , liestinė neapibrėžta, o tai vyksta kampuose 90°+180° k , k∈Z (π /2+π k rad). Iš tiesų, esant tokiems sukimosi kampams, išraiška tgα=y/x neturi prasmės, nes joje yra dalijimas iš nulio. Kalbant apie kotangentą, jis neapibrėžtas tokiems kampams α, kuriuose pradžios taškas eina į tašką, kurio ordinatė yra nulinė (1, 0) arba (−1, 0), o tai yra 180° k kampų atveju, k ∈Z (π k rad).

Taigi sinusas ir kosinusas yra apibrėžti bet kokiems sukimosi kampams, liestinė apibrėžiama visiems kampams, išskyrus 90°+180° k , k∈Z (π/2+π k rad), o kotangentas yra visiems kampams, išskyrus 180 ° ·k , k∈Z (π·k rad).

Mums jau žinomi žymėjimai atsiranda apibrėžimuose sin, cos, tg ir ctg, jie taip pat naudojami žymėti sukimosi kampo sinusą, kosinusą, liestinę ir kotangentą (kartais galite rasti žymėjimą tan ir cot, atitinkantį liestinę ir kotangentas). Taigi 30 laipsnių sukimosi kampo sinusas gali būti parašytas kaip sin30°, įrašai tg(−24°17′) ir ctgα atitinka sukimosi kampo liestinę −24° 17 minučių ir sukimosi kampo α kotangentą. . Prisiminkite, kad rašant kampo radianinį matą, užrašas „rad“ dažnai praleidžiamas. Pavyzdžiui, trijų pi radų sukimosi kampo kosinusas paprastai žymimas cos3 π .

Apibendrinant šią pastraipą, verta paminėti, kad kalbant apie sukimosi kampo sinusą, kosinusą, liestinę ir kotangentą, frazė „sukimosi kampas“ arba žodis „sukimas“ dažnai praleidžiama. Tai yra, vietoj frazės „sukimosi kampo sinusas alfa“ dažniausiai vartojamas posakis „alfa kampo sinusas“ arba dar trumpesnis – „alfa sinusas“. Tas pats pasakytina apie kosinusą, tangentą ir kotangentą.

Taip pat tarkime, kad stačiojo trikampio smailaus kampo sinuso, kosinuso, liestinės ir kotangento apibrėžimai atitinka ką tik pateiktus sukimosi kampo sinuso, kosinuso, liestinės ir kotangento apibrėžimus, kurie svyruoja nuo 0 iki 90 laipsnių. Mes tai pagrįsime.

Skaičiai

Apibrėžimas.

Skaičiaus sinusas, kosinusas, liestinė ir kotangentas t yra skaičius, lygus sukimosi kampo sinusui, kosinusui, tangentui ir kotangentui atitinkamai t radianais.

Pavyzdžiui, 8 π kosinusas pagal apibrėžimą yra skaičius, lygus 8 π rad kampo kosinusui. O kampo kosinusas 8 π rad lygus vienetui, todėl skaičiaus 8 π kosinusas lygus 1.

Yra ir kitas skaičiaus sinuso, kosinuso, liestinės ir kotangento apibrėžimo būdas. Jį sudaro tai, kad kiekvienam realiajam skaičiui t priskiriamas vienetinio apskritimo taškas, kurio centras yra stačiakampės koordinačių sistemos pradžioje, o sinusas, kosinusas, liestinė ir kotangentas nustatomi per šio taško koordinates. Pakalbėkime apie tai išsamiau.

Parodykime, kaip nustatoma realiųjų skaičių ir apskritimo taškų atitiktis:

• skaičiui 0 priskiriamas pradžios taškas A(1, 0) ;
• teigiamas skaičius t yra susietas su vienetinio apskritimo tašku, į kurį pateksime, jei apeisime apskritimą nuo pradžios taško prieš laikrodžio rodyklę ir eisime t ilgio taku;
• neigiamas skaičius t yra susietas su vienetinio apskritimo tašku, į kurį pateksime, jei apvažiuosime apskritimą nuo pradžios taško pagal laikrodžio rodyklę ir eisime |t| .

Dabar pereikime prie skaičiaus t sinuso, kosinuso, liestinės ir kotangento apibrėžimų. Tarkime, kad skaičius t atitinka apskritimo tašką A 1 (x, y) (pavyzdžiui, skaičius &pi/2; atitinka tašką A 1 (0, 1) ).

Apibrėžimas.

Skaičiaus sinusas t yra vienetinio apskritimo taško, atitinkančio skaičių t, ordinatė, tai yra sint=y .

Apibrėžimas.

Skaičiaus kosinusas t vadinama vienetinio apskritimo taško, atitinkančio skaičių t, abscise, tai yra kaina=x .

Apibrėžimas.

Skaičiaus liestinė t yra vienetinio apskritimo taško, atitinkančio skaičių t, ordinatės ir abscisių santykis, tai yra tgt=y/x. Kitoje lygiavertėje formuluotėje skaičiaus t liestinė yra šio skaičiaus sinuso ir kosinuso santykis, ty tgt=sint/cost .

Apibrėžimas.

Skaičiaus kotangentas t yra abscisių santykis su vienetinio apskritimo taško, atitinkančio skaičių t, ordinatės, tai yra, ctgt=x/y. Kita formuluotė yra tokia: skaičiaus t liestinė yra skaičiaus t kosinuso ir skaičiaus t sinuso santykis: ctgt=kaina/sint .

Atkreipiame dėmesį, kad ką tik pateikti apibrėžimai atitinka šio poskyrio pradžioje pateiktą apibrėžimą. Iš tiesų, vienetinio apskritimo taškas, atitinkantis skaičių t, sutampa su tašku, gautu sukant pradinį tašką t radianų kampu.

Taip pat verta paaiškinti šį dalyką. Tarkime, kad turime sin3 įrašą. Kaip suprasti, ar kalbama apie skaičiaus 3 sinusą, ar apie 3 radianų sukimosi kampo sinusą? Paprastai tai aišku iš konteksto, kitu atveju tikriausiai nesvarbu.

Kampinio ir skaitinio argumento trigonometrinės funkcijos

Pagal ankstesnėje pastraipoje pateiktus apibrėžimus kiekvienas sukimosi kampas α atitinka tiksliai apibrėžtą reikšmę sin α , taip pat reikšmę cos α . Be to, visi sukimosi kampai, išskyrus 90°+180° k , k∈Z (π/2+π k rad), atitinka reikšmes tgα ir, išskyrus 180° k , k∈Z (π k rad ) yra ctgα reikšmės. Todėl sinα, cosα, tgα ir ctgα yra kampo α funkcijos. Kitaip tariant, tai yra kampinio argumento funkcijos.

Panašiai galime kalbėti apie skaitinio argumento sinuso, kosinuso, tangento ir kotangento funkcijas. Iš tiesų, kiekvienas tikrasis skaičius t atitinka tiksliai apibrėžtą sint reikšmę, taip pat kaštus. Be to, visi skaičiai, išskyrus π/2+π·k , k∈Z atitinka reikšmes tgt , o skaičiai π·k , k∈Z atitinka reikšmes ctgt .

Vadinamos funkcijos sinusas, kosinusas, liestinė ir kotangentas pagrindinės trigonometrinės funkcijos.

Iš konteksto paprastai aišku, kad kalbame apie kampinio argumento arba skaitinio argumento trigonometrines funkcijas. Kitu atveju nepriklausomą kintamąjį galime laikyti ir kampo matu (kampo argumentu), ir skaitiniu argumentu.

Tačiau mokykloje daugiausia tiriamos skaitinės funkcijos, tai yra funkcijos, kurių argumentai ir atitinkamos funkcijų reikšmės yra skaičiai. Todėl jei kalbame apie funkcijas, patartina trigonometrines funkcijas laikyti skaitinių argumentų funkcijomis.

Geometrijos ir trigonometrijos apibrėžimų jungtis

Jei atsižvelgsime į sukimosi kampą α nuo 0 iki 90 laipsnių, tada sukimosi kampo sinuso, kosinuso, tangento ir kotangento apibrėžimo trigonometrijos duomenys visiškai atitinka sinuso, kosinuso apibrėžimus. , stačiojo trikampio smailiojo kampo liestinė ir kotangentas, kurios pateiktos geometrijos kurse. Pagrįskime tai.

Stačiakampėje Dekarto koordinačių sistemoje Oxy nubrėžkite vienetinį apskritimą. Atkreipkite dėmesį į pradžios tašką A(1, 0) . Pasukime jį kampu α nuo 0 iki 90 laipsnių, gausime tašką A 1 (x, y) . Numeskime statmeną A 1 H nuo taško A 1 į Ox ašį.

Nesunku pastebėti, kad stačiakampiame trikampyje kampas A 1 OH lygus sukimosi kampui α, šiam kampui gretimos kojos OH ilgis lygus taško A 1 abscisei, tai yra |OH |=x, kampui priešingos kojos A 1 H ilgis lygus taško A 1 ordinatėms, tai yra |A 1 H|=y , o hipotenuzės ilgis OA 1 lygus vienetui , nes tai yra vienetinio apskritimo spindulys. Tada pagal geometrijos apibrėžimą smailaus kampo α sinusas stačiakampiame trikampyje A 1 OH yra lygus priešingos kojos ir hipotenuzos santykiui, tai yra sinα=|A 1 H|/|OA 1 |= y/1=y . Ir pagal trigonometrijos apibrėžimą, sukimosi kampo α sinusas yra lygus taško A 1 ordinatei, tai yra sinα=y. Tai rodo, kad stačiojo trikampio smailiojo kampo sinuso apibrėžimas yra lygiavertis sukimosi kampo α sinuso apibrėžimui, kai α nuo 0 iki 90 laipsnių.

Panašiai galima parodyti, kad smailiojo kampo α kosinuso, liestinės ir kotangento apibrėžimai atitinka sukimosi kampo α kosinuso, liestinės ir kotangento apibrėžimus.

Bibliografija.

1. Geometrija. 7-9 klasės: studijos. bendrajam lavinimui institucijos / [L. S. Atanasjanas, V. F. Butuzovas, S. B. Kadomcevas ir kiti]. – 20-asis leidimas. M.: Išsilavinimas, 2010. - 384 p.: iliustr. - ISBN 978-5-09-023915-8.
2. Pogorelovas A.V. Geometrija: Proc. 7-9 ląstelėms. bendrojo išsilavinimo institucijos / A. V. Pogorelovas. - 2 leidimas - M.: Švietimas, 2001. - 224 p.: iliustr. - ISBN 5-09-010803-X.
3. Algebra ir elementariosios funkcijos: Vadovėlis vidurinės mokyklos 9 klasių mokiniams / E. S. Kochetkov, E. S. Kochetkova; Redagavo fizinių ir matematikos mokslų daktaras O. N. Golovinas – 4 leidimas. Maskva: Švietimas, 1969 m.
4. Algebra: Proc. 9 ląstelėms. vid. mokykla / Yu. N. Makaryčiovas, N. G. Mindjukas, K. I. Neškovas, S. B. Suvorova; Red. S. A. Teljakovskis.- M.: Švietimas, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
5. Algebra ir analizės pradžia: Proc. 10-11 ląstelių. bendrojo išsilavinimo institucijos / A. N. Kolmogorovas, A. M. Abramovas, Yu. P. Dudnicynas ir kt.; Red. A. N. Kolmogorova.- 14 leid.- M.: Švietimas, 2004.- 384 p.: iliustr.- ISBN 5-09-013651-3.
6. Mordkovičius A. G. Algebra ir analizės pradžia. 10 klasė. 14 val. 1 dalis: vadovėlis švietimo įstaigoms (profilio lygis) / A. G. Mordkovich, P. V. Semenov. - 4-asis leidimas, pridėti. - M.: Mnemosyne, 2007. - 424 p.: iliustr. ISBN 978-5-346-00792-0.
7. Algebra ir matematinės analizės pradžia. 10 klasė: vadovėlis. bendrajam lavinimui institucijos: pagrindinės ir profilio. lygiai /[Yu. M. Kolyaginas, M. V. Tkačiova, N. E. Fedorova, M. I. Šabuninas]; red. A. B. Žižčenka. - 3 leidimas. - I .: Švietimas, 2010. - 368 p.: Ill. - ISBN 978-5-09-022771-1.
8. Bašmakovas M.I. Algebra ir analizės pradžia: Proc. 10-11 ląstelių. vid. mokykla - 3 leidimas. - M.: Švietimas, 1993. - 351 p.: iliustr. - ISBN 5-09-004617-4.
9. Gusevas V. A., Mordkovičius A. G. Matematika (vadovas stojantiesiems į technikos mokyklas): Proc. pašalpa.- M.; Aukščiau mokykla, 1984.-351 p., iliustr.

Iš grafikų matyti, kad:

1. Sinuso ir kosinuso grafikai svyruoja nuo -1 iki 1
2. Kosinuso kreivė yra tokios pat formos kaip sinuso kreivė, bet jos atžvilgiu yra pasislinkusi 90 o
3. Sinuso ir kosinuso kreivės yra ištisinės ir kartojasi 360 o periodu, liestinės kreivė turi nutrūkimų ir kartojasi su 180 o periodu.

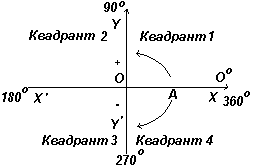Ant pav. kairėje pavaizduotos statmenos ašys XX" ir YY"; susikertanti ištakoje O. Dirbant su grafikais matavimai į dešinę ir aukštyn nuo O laikomi teigiamais, į kairę ir žemyn nuo O – neigiamais. Leiskite OA laisvai suktis O atžvilgiu. Kai OA pasukama prieš laikrodžio rodyklę, išmatuotas kampas laikomas teigiamu, o sukamas pagal laikrodžio rodyklę – neigiamas.

Tvarkaraštis. teigiamas ar neigiamas
kryptimi sukamaisiais judesiais.

Tegul OA sukasi prieš laikrodžio rodyklę taip, kad Θ 1 būtų bet koks kampas pirmajame kvadrante, ir sukonstruokite statmeną AB, kad gautumėte stačiakampį trikampį OAB pav. paliko. Kadangi visos trys trikampio kraštinės yra teigiamos, trigonometrinės funkcijos sinusas, kosinusas ir liestinė pirmajame kvadrante bus teigiamos. (Atkreipkite dėmesį, kad OA ilgis visada yra teigiamas, nes tai yra apskritimo spindulys.)
Tegul OA sukasi toliau taip, kad Θ 2 būtų bet koks kampas antrajame kvadrante, ir sukonstruokite AC taip, kad susidarytų stačiakampis trikampis OAC. Tada sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Tegul OA sukasi toliau taip, kad Θ 3 būtų bet koks kampas trečiajame kvadrante, ir sukonstruokite AD taip, kad susidarytų stačiakampis trikampis OAD. Tada sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

Tvarkaraštis. Kampų pastatymas
įvairūs kvadrantai.

Tegul OA sukasi toliau taip, kad Θ 4 būtų bet koks ketvirtojo kvadranto kampas, ir sukonstruokite AE taip, kad susidarytų stačiakampis trikampis OAE. Tada sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

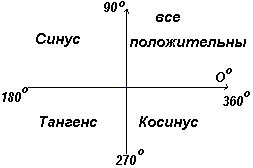
Pirmajame kvadrante visos trigonometrinės funkcijos turi teigiamas reikšmes, antrajame – teigiamas tik sinusas, trečiame – tik liestinė, ketvirtame – tik kosinusas, kuris parodytas 1 pav. paliko.

Žinios apie savavališko dydžio kampus būtinos, kai randame, pavyzdžiui, visus kampus nuo 0 o iki 360 o, kurių sinusas yra, tarkime, 0,3261. Į skaičiuotuvą įvedę 0,3261 ir paspaudę sin -1 mygtuką gausime atsakymą 19,03 o. Tačiau yra antras kampas nuo 0 o iki 360 o, kurio skaičiuotuvas nerodys. Sinusas taip pat yra teigiamas antrajame kvadrante. Kitas kampas parodytas fig. žemiau kaip kampas Θ, kur Θ=180 o - 19,03 o = 160,97 o . Taigi 19,03 o ir 160,97 o yra kampai diapazone nuo 0 o iki 360 o, kurių sinusas yra 0,3261.

Būk atsargus! Skaičiuoklė pateikia tik vieną iš šių reikšmių. Antroji vertė turėtų būti nustatyta pagal savavališko dydžio kampų teoriją.

1 pavyzdys

Raskite visus kampus nuo 0 o iki 360 o, kurių sinusas yra -0,7071

Sprendimas:
Kampai, kurių sinusas yra -0,7071 o, yra trečiajame ir ketvirtajame kvadrantuose, nes tuose kvadrantuose sinusas yra neigiamas (žr. paveikslą kairėje).

Tvarkaraštis. Visų kampų paieška pagal
duota sinuso reikšmė (pavyzdys)

Iš toliau pateikto paveikslo Θ = arcsin 0,7071 = 45 o . Du kampai diapazone nuo 0 o iki 360 o, kurių sinusas yra -0,7071, yra 180 o +45 o \u003d 225 o ir 360 o - 45 o \u003d 315 o.

Pastaba. Skaičiuoklė pateikia tik vieną atsakymą.
Tvarkaraštis. Visų kampų paieška pagal
duota sinuso reikšmė (pavyzdys)

2 pavyzdys

Raskite visus kampus nuo 0 o iki 360 o, kurių liestinė yra 1,327.

Sprendimas:
Pirmajame ir trečiajame kvadrantuose liestinė teigiama – pav. paliko.
Tvarkaraštis. Visų kampų paieška pagal

Iš žemiau esančio paveikslo Θ = arctan1,327= 53 o .
Du kampai diapazone nuo 0 o iki 360 o, kurių liestinė yra 1,327, yra 53 o ir 180 o + 53 o, t.y. 233o.
Tvarkaraštis. Visų kampų paieška pagal
duota liestinės reikšmė (pavyzdys)

Leiskite ARBA pav. kairėje yra vieneto ilgio vektorius, laisvai besisukantis prieš laikrodžio rodyklę aplink O. Vienu apsisukimu susidaro apskritimas, parodytas fig. ir padalintas iš 15 o sektorių. Kiekvienas spindulys turi horizontalią ir vertikalią sudedamąsias dalis. Pavyzdžiui, 30 o vertikalus komponentas yra TS, o horizontalus komponentas yra OS.

Iš trigonometrinių funkcijų apibrėžimo
sin30 o =TS/TO=TS/1, t.y. TS=sin30o ir cos30 o =OS/TO=OS/1, t.y. OS = cos30o

Vertikalioji komponentė TS gali būti nubraižyta kaip T"S", kuri yra lygi vertei, atitinkančiai 30° kampą y ir x kampo diagramoje. Jei visi vertikalūs komponentai, tokie kaip TS, perkeliami į grafiką, bus gauta sinusoidė, parodyta Fig. aukščiau.

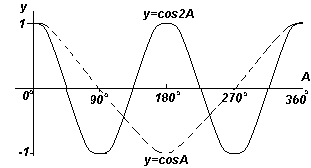
Jei visi horizontalūs komponentai, pvz., OS, yra projektuojami į y ir x diagramą, gausite kosinuso bangą. Šias projekcijas lengva vizualizuoti perbraižant apskritimą, kurio spindulys ARBA ir kampai iš vertikalios pusės, kaip parodyta paveikslėlyje kairėje.
Iš pav. kairėje pusėje matote, kad sinusoidė turi tokią pačią formą kaip ir kosinuso banga, bet pasislinkusi 90 o .

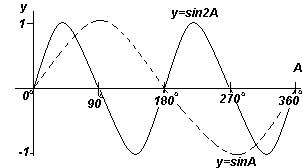Periodinės funkcijos ir laikotarpis
Kiekviena iš funkcijų grafikų, parodytų keturiuose Fig. aukščiau, kartojasi didėjant kampui A, todėl jie vadinami periodines funkcijas.
Funkcijos y=sinA ir y=cosA kartojasi kas 360 o (arba 2π radianus), todėl 360 o vadinama laikotarpįšias funkcijas. Funkcijos y=sin2A ir y=cos2A kartojasi kas 180 o (arba π radianų), taigi 180 o yra šių funkcijų periodas.
Apskritai, jei y=sinpA ir y=cospA (kur p yra konstanta), tai funkcijos periodas yra 360 o /p (arba 2π/p radianų). Todėl, jei y=sin3A, tai šios funkcijos periodas yra 360 o /3= 120 o , jei y=cos4A, tai šios funkcijos periodas yra 360 o /4= 90 o .

Amplitudė
Amplitudė vadinama maksimalia sinusoido verte. Kiekvienos iš 1–4 grafikų amplitudė yra +1 (t. y. jos svyruoja tarp +1 ir -1). Tačiau, jei y = 4sinA, kiekviena sinA reikšmė padauginama iš 4, taigi maksimali amplitudės reikšmė yra 4. Panašiai, kai y = 5cos2A, amplitudė yra 5, o periodas yra 360 o /2 = 180 o .

3 pavyzdys
Sukurkite y=3sin2A diapazone nuo A= 0 o iki A=360 o .

Sprendimas:
Amplitudė =3, periodas = 360 o /2 =180 o .

4 pavyzdys
Nubraižykite y=4cos2x diapazone nuo x=0 o iki x=360 o

Sprendimas:
Amplitudė = 4. periodas = 360 o /2 =180 o .

Atsilikimo ir švino kampai
Sinuso ir kosinuso kreivės ne visada prasideda nuo 0 o . Kad būtų atsižvelgta į šią aplinkybę, periodinė funkcija vaizduojama kaip y=sin(A± α), kur α yra fazės poslinkis y=sinA ir y=cosA atžvilgiu.

Sudarę reikšmių lentelę, galite nubraižyti funkciją y=sin(A-60 o), parodytą fig. paliko. Jei y=sinA kreivė prasideda nuo 0 o , tai kreivė y=sin(A-60 o ) prasideda nuo 60 o (ty jos nulinė reikšmė yra 60 o į dešinę). Taigi sakoma, kad y = sin(A-60 o) vėlai y=sinA atžvilgiu 60°.
Tvarkaraštis. y=sin(A-60 o) (sinuso banga).

Sudarę reikšmių lentelę, galite nubraižyti funkciją y=cos(A+45 o), parodytą fig. žemiau.
Jei kreivė y=cosA prasideda nuo 0 o , tai kreivė y=cos(A+45 o) prasideda 45 o į kairę (ty jos nulinė reikšmė yra 45 o anksčiau).
Taigi sakoma, kad sklypas yra y=cos(A+45 o) prieš diagrama y=cosA 45° kampu.
Tvarkaraštis. y=cos(A+45 o) (kosinusas).

Apskritai grafikas y=sin(A-α) atsilieka nuo y=sinA kampu α.
Kosinuso banga yra tokios pat formos kaip sinusoidė, bet prasideda 90 o į kairę, t.y. lenkia ją 90 o . Todėl cosA=sin(A+90o).

5 pavyzdys
Nubraižykite y=5sin(A+30 o) intervale nuo A=0 o iki A=360 o

Sprendimas:
Amplitudė = 5, periodas = 360 o /1 = 360 o .
5sin(A+30 o) pirmauja 5sinA 30 o t.y. prasideda 30 o anksčiau.
Grafikas y=5sin(A+30 o) (sinusoidas).

6 pavyzdys
Nubraižykite y=7sin(2A-π/3) intervale nuo A=0 o iki A=360 o .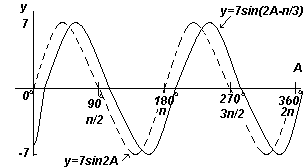

Sprendimas:
Amplitudė = 7, periodas = 2π/2= π radianai
Apskritai y=sin(pt-α) atsilieka nuo y=sinpt α/p, todėl 7sin(2A-π/3) atsilieka nuo 7sin2A (π/3)/2, t.y. už π/6 radianų arba 30 o

Asin(ωt±α) formos sinusoidas. fazės kampas. Fazės poslinkis.

Leiskite ARBA pav. kairėje yra vektorius, laisvai besisukantis prieš laikrodžio rodyklę aplink O ω radianų/s greičiu. Besisukantis vektorius vadinamas fazės vektorius. Po t sekundžių OR pasisuks kampu ωt radianais (paveiksle kairėje tai kampas TOR). Jei ST statomas statmenai OR, tai sinωt=ST/OT, t.y. ST = OTsinωt.
Jei visi tokie vertikalūs komponentai yra projektuojami į y ir ωt diagramą, bus gauta sinusoidė su amplitudė OR.

Jei fazės vektorius ARBA padaro vieną apsisukimą (ty 2π radianus) per T sekundes, tai kampinis greitis ω=2π/T rad/s, iš kur
Т=2π/ ω (s), kur
T yra laikotarpį
Vadinamas pilnų laikotarpių, praeinančių per 1 sekundę, skaičius dažnis f.
Dažnis = (periodų skaičius)/(sekundė) = 1/ T = ω/2π Hz, tie. f= ω/2π Hz
Todėl kampinis greitis
ω=2πf rad/s.

Jei apskritai sinusoidinė funkcija atrodo taip y=sin(ωt± α), tada
A – amplitudė
ω – kampinis greitis
2π/ ω - periodas T, s
ω/2π - dažnis f, Hz
α yra švino arba vėlavimo kampas (santykis su y=Аsinωt) radianais, jis taip pat vadinamas faziniu kampu.

7 pavyzdys
Kintamoji srovė pateikiama kaip i=20sin(90πt+0,26) amperų. Nustatykite amplitudę, periodą, dažnį ir fazės kampą (laipsniais)

Sprendimas:
i \u003d 20sin (90πt + 0,26) A, todėl
amplitudė yra 20 A
kampinis greitis ω= 90π, todėl
laikotarpis T= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
dažnis f\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
fazės kampas α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.

8 pavyzdys
Virpesių mechanizmo didžiausias poslinkis yra 3 m, o dažnis - 55 Hz. Laike t=0 poslinkis yra 100 cm. Poslinkį išreikškite bendra forma Аsin(ωt± α).

Sprendimas
Amplitudė = didžiausias poslinkis = 3 m
Kampinis greitis ω=2πf = 2π(55) = 110 rad/s
Todėl poslinkis yra 3sin(110πt + α) m.
Esant t = 0 poslinkis = 100 cm = 1 m.
Todėl 1= 3sin(0 + α), t.y. sinα=1/3=0,33
Todėl α=arcsin0,33=19 o
Taigi poslinkis yra 3sin(110 πt + 0,33).

9 pavyzdys
Momentinės įtampos reikšmė kintamosios srovės grandinėje bet kuriomis t sekundėmis pateikiama kaip v=350sin(40πt-0,542)V. Rasti:
a) Amplitudė, periodas, dažnis ir fazės kampas (laipsniais)
b) įtampos reikšmė, kai t = 0
c) įtampos reikšmė esant t = 10 ms
d) laikas, per kurį įtampa pirmą kartą pasiekia 200 V.
Sprendimas:
a) Amplitudė 350 V, kampinis greitis ω=40π
Vadinasi,
laikotarpis Т=2π/ ω=2π/40π=0,05 s =50 ms
dažnis f=1/T=1/0,05=20 Hz
fazės kampas \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o su vėlavimu, palyginti su v \u003d 350sin (40πt)
b) Jei t \u003d 0, tada v \u003d 350sin (0-0,542) \u003d 350sin (-31 o) \u003d -180,25 V
c) Jei t \u003d 10 ms, tada v \u003d 350sin (40π10 / 10 3 -0,542) \u003d 350sin (0,714) \u003d 350sin41 o \u003d V 22
d) Jei v = 200 IR, tada 200 = 350 sin(40πt-0,542) 200/350 = sin (40πt-0,542)

Tvarkaraštis. Virpesių mechanizmas
(pavyzdys, sinusoidas).

v=350sin(40πt-0,542) Todėl (40πt-0,542)=arcsin200/350=35 o arba 0,611 rad.
40πt= 0,611+0,542=1,153.
Taigi, jei v = 200 V, laikas t = 1,153/40π = 9,179 ms

Geometrinis sinuso ir kosinuso apibrėžimas

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α yra kampas, išreikštas radianais.

Sinusas yra kampo α tarp stačiojo trikampio hipotenuzės ir atšakos trigonometrinė funkcija, lygi priešingos kojos ilgio santykiui |BC| iki hipotenuzės ilgio |AB|.

Kosinusas (cos α) yra trigonometrinė kampo α tarp stačiojo trikampio hipotenuzės ir atšakos funkcija, lygi gretimos kojos ilgio santykiui |AC| iki hipotenuzės ilgio |AB|.

Trigonometrinis apibrėžimas

Naudodami aukščiau pateiktas formules galite rasti smailaus kampo sinusus ir kosinusus. Bet jūs turite išmokti apskaičiuoti savavališko dydžio kampo sinusus ir kosinusus. Stačiakampis trikampis tokios galimybės nesuteikia (pavyzdžiui, bukas kampas jame negali būti); todėl reikalingas bendresnis sinuso ir kosinuso apibrėžimas, įtraukiant šias formules kaip ypatingą atvejį.

Į pagalbą ateina trigonometrinis ratas. Leiskite pateikti tam tikrą kampą; jis atitinka to paties pavadinimo tašką trigonometriniame apskritime.

Ryžiai. 2. Trigonometrinis sinuso ir kosinuso apibrėžimas

Kampo kosinusas yra taško abscisė. Kampo sinusas yra taško ordinatė.

Ant pav. 2 kampas imamas smailiu, ir nesunku suprasti, kad šis apibrėžimas sutampa su bendruoju geometriniu apibrėžimu. Iš tiesų, matome stačiakampį trikampį su vienetine hipotenuze O ir smailiu kampu. Gretima šio trikampio kojelė yra cos (plg. su 1 pav.) ir tuo pačiu taško abscisė; priešinga kojelė yra nuodėmė (kaip 1 pav.) ir kartu taško ordinatė.

Tačiau dabar mūsų nebevaržo pirmasis ketvirtis ir gauname galimybę išplėsti šį apibrėžimą bet kokiu kampu. Ant pav. 3 parodyta, koks yra kampo sinusas ir kosinusas antrajame, trečiame ir ketvirtame ketvirčiuose.

Ryžiai. 3. Sinusas ir kosinusas II, III ir IV ketvirčiuose

Sinuso ir kosinuso lentelės reikšmės

Nulinis kampas \(\LARGE 0^(\circ ) \)

Taško 0 abscisė lygi 1 , taško 0 ordinatė lygi 0 . Vadinasi,

cos 0 = 1 sin 0 = 0

4 pav. Nulinis kampas

Kampas \(\LARGE \frac(\pi)(6) = 30^(\circ ) \)

Matome stačią trikampį su vienetine hipotenuze ir smailiu 30° kampu. Kaip žinote, koja, esanti priešais 30 ° kampą, yra lygi pusei hipotenuzės 1; kitaip tariant, vertikali kojelė yra lygi 1/2 ir todėl

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Horizontaliąją koją randame naudodami Pitagoro teoremą (arba, kas yra ta pati, randame kosinusą pagal pagrindinę trigonometrinę tapatybę):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 Kodėl taip atsitinka? Iškirpkite lygiakraštį trikampį su 2 kraštine išilgai jo aukščio! Jis skyla į du stačiuosius trikampius su 2 hipotenuze, smailiu kampu 30° ir mažesne 1 kojele.

5 pav. Kampas π / 6

Kampas \(\LARGE \frac(\pi)(4) = 45^(\circ ) \)

Šiuo atveju stačiakampis trikampis yra lygiašonis; 45° kampo sinusas ir kosinusas yra lygūs vienas kitam. Kol kas pažymėkime juos x. Mes turime:

\[ x^(2) + x^(2) = 1 \]

iš kur \(x=\frac(\sqrt(2) )(2) \). Vadinasi,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

5 pav. Kampas π / 4

Sinuso ir kosinuso savybės

Priimti pavadinimai

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Periodiškumas

Funkcijos y = sin x ir y = cos x yra periodinės, kurių periodas yra 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Paritetas

Sinuso funkcija yra nelyginė. Kosinuso funkcija yra lygi.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Apibrėžimo ir vertybių sritys, ekstremumai, padidėjimas, sumažėjimas

Pagrindinės sinuso ir kosinuso savybės pateiktos lentelėje ( n- sveikasis skaičius).

	\(\mažas< x < \)	\(\small -\pi + 2\pi n \) \(\mažas< x < \) \(\small 2\pi n \)
Mažėjantis	\(\small \dfrac(\pi)2 + 2\pi n \)\(\mažas< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \)	\(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \)
Maksimumai, \(\mažas x = \) \(\small \dfrac(\pi)2 + 2\pi n \)	\(\mažas x = 2\pi n \)
Minimalus, \(\mažas x = \) \(\small -\dfrac(\pi)2 + 2\pi n \)	\(\mažas x = \) \(\mažas \pi + 2\pi n \)
Nuliai, \(\small x = \pi n \)	\(\small x = \dfrac(\pi)2 + \pi n \)
Sankirtos taškai su y ašimi, x = 0	y=0	y = 1

Pagrindinės formulės, kuriose yra sinusas ir kosinusas

Kvadratų suma

\(\sin^2 x + \cos^2 x = 1 \)

Sinuso ir kosinuso sumos ir skirtumo formulės

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Sinusų ir kosinusų sandaugos formulės

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)

Sumos ir skirtumo formulės

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Sinuso raiška per kosinusą

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\(2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Kosinuso raiška per sinusą

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Išraiška liestine

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

At \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

At \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Sinusų ir kosinusų, liestinių ir kotangentų lentelė

Šioje lentelėje parodytos kai kurių argumento verčių sinusų ir kosinusų reikšmės.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="(!LANG: sinusų ir kosinusų lentelė" title="Sinusų ir kosinusų lentelė" ]!}

Išraiškos per sudėtingus kintamuosius

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Eulerio formulė

\(e^(iz) = \cos z + i \sin z \)

Išraiškos pagal hiperbolines funkcijas

\(\sin iz = i \shz \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Dariniai

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Formulių išvedimas >>>

n-osios eilės vediniai:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Integralai

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Taip pat žiūrėkite skyrių Neapibrėžtinių integralų lentelė >>>

Išplėtimas į serijas

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Sekantas, kosekantas

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

Atvirkštinės funkcijos

Atvirkštinės sinuso ir kosinuso funkcijos yra atitinkamai arcsinusas ir arkosinusas.

Arčinas, arcsin

\(y = \arcsin x \) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

Arkosinas, arkosas

\(y = \arccos x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Nuorodos:
I.N. Bronšteinas, K.A. Semendyaev, Matematikos vadovas inžinieriams ir aukštųjų mokyklų studentams, Lan, 2009 m.

„Javascript“ jūsų naršyklėje išjungtas.
„ActiveX“ valdikliai turi būti įjungti, kad būtų galima atlikti skaičiavimus!

Centruota taške A.
α yra kampas, išreikštas radianais.

Tangentas ( tgα) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi priešingos kojos ilgio santykiui |BC| iki gretimos kojos ilgio |AB| .

Kotangentas ( ctgα) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi gretimos kojos ilgio santykiui |AB| į priešingos kojos ilgį |BC| .

Tangentas

Kur n- visas.

Vakarų literatūroje liestinė žymima taip:
.
;
;
.

Tangentinės funkcijos grafikas, y = tg x

Kotangentas

Kur n- visas.

Vakarų literatūroje kotangentas žymimas taip:
.
Taip pat buvo priimtas toks užrašas:
;
;
.

Kotangentinės funkcijos grafikas, y = ctg x

Tangento ir kotangento savybės

Periodiškumas

Funkcijos y= tg x ir y= ctg x yra periodiniai su periodu π.

Paritetas

Funkcijos liestinė ir kotangentas yra nelyginės.

Apibrėžimo ir vertybių sritys, kylančios, mažėjančios

Funkcijos tangentas ir kotangentas yra ištisinės savo apibrėžimo srityje (žr. tęstinumo įrodymą). Pagrindinės liestinės ir kotangento savybės pateiktos lentelėje ( n- sveikasis skaičius).

	y= tg x	y= ctg x
Taikymo sritis ir tęstinumas
Vertybių diapazonas	-∞ < y < +∞	-∞ < y < +∞
Kylantis		-
Mažėjantis	-
Kraštutinumai	-	-
Nuliai, y= 0
Sankirtos taškai su y ašimi, x = 0	y= 0	-

Formulės

Išraiškos sinuso ir kosinuso terminais

; ;
; ;
;

Sumos ir skirtumo liestinės ir kotangento formulės

Pavyzdžiui, likusias formules lengva gauti

Tangentų sandauga

Tangentų sumos ir skirtumo formulė

Šioje lentelėje parodytos kai kurių argumento verčių liestinių ir kotangentų reikšmės.

Išraiškos kompleksiniais skaičiais

Išraiškos pagal hiperbolines funkcijas

;
;

Dariniai

; .

.
N-osios eilės išvestinė funkcijos kintamojo x atžvilgiu:
.
Tangento > > > formulių išvedimas ; kotangentui >>>

Integralai

Išplėtimas į serijas

Norėdami gauti x laipsnio liestinės išplėtimą, turite paimti keletą funkcijų plėtimosi narių laipsnių eilutėje nuodėmė x ir cos x ir padalinti šiuos daugianario vieni į kitus , . Dėl to gaunamos tokios formulės.

Prie .

adresu .
kur B n- Bernulio skaičiai. Jie nustatomi iš pasikartojimo santykio:
;
;
kur .
Arba pagal Laplaso formulę:

Atvirkštinės funkcijos

Atvirkštinės liestinės ir kotangentinės funkcijos yra atitinkamai arktangentas ir arkotangentas.

Arktangentas, arktg

, kur n- visas.

Lanko liestinė, arcctg

, kur n- visas.

Nuorodos:
I.N. Bronšteinas, K.A. Semendyaev, Matematikos vadovas inžinieriams ir aukštųjų mokyklų studentams, Lan, 2009 m.
G. Korn, Matematikos vadovas tyrėjams ir inžinieriams, 2012 m.

Centruota taške A.
α yra kampas, išreikštas radianais.

Apibrėžimas
Sinusas yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi priešingos kojos ilgio santykiui |BC| iki hipotenuzės ilgio |AC|.

Kosinusas (cos α) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi gretimos kojos ilgio santykiui |AB| iki hipotenuzės ilgio |AC|.

Priimti pavadinimai

;
;
.

;
;
.

Sinuso funkcijos grafikas, y = sin x

Kosinuso funkcijos grafikas, y = cos x

Sinuso ir kosinuso savybės

Periodiškumas

Funkcijos y= nuodėmė x ir y= cos x periodinis su tašku 2 pi.

Paritetas

Sinuso funkcija yra nelyginė. Kosinuso funkcija yra lygi.

Apibrėžimo ir vertybių sritis, ekstremumai, padidėjimas, sumažėjimas

Funkcijos sinusas ir kosinusas yra tolydžios savo apibrėžimo srityje, tai yra, visiems x (žr. tęstinumo įrodymą). Pagrindinės jų savybės pateiktos lentelėje (n – sveikas skaičius).

	y= nuodėmė x	y= cos x
Taikymo sritis ir tęstinumas	- ∞ < x < + ∞	- ∞ < x < + ∞
Vertybių diapazonas	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Kylantis
Mažėjantis
Maksimumai, y= 1
Minimalus, y = - 1
Nuliai, y= 0
Sankirtos taškai su y ašimi, x = 0	y= 0	y= 1

Pagrindinės formulės

Sinuso ir kosinuso kvadrato suma

Sumos ir skirtumo sinuso ir kosinuso formulės

;
;

Sinusų ir kosinusų sandaugos formulės

Sumos ir skirtumo formulės

Sinuso raiška per kosinusą

;
;
;
.

Kosinuso raiška per sinusą

;
;
;
.

Išraiška liestine

; .

Mes turime:
; .

adresu:
; .

Sinusų ir kosinusų, liestinių ir kotangentų lentelė

Šioje lentelėje parodytos kai kurių argumento verčių sinusų ir kosinusų reikšmės.

Išraiškos per sudėtingus kintamuosius

;

Eulerio formulė

Išraiškos pagal hiperbolines funkcijas

;
;

Dariniai

; . Formulių išvedimas >>>

n-osios eilės vediniai:
{ -∞ < x < +∞ }

Sekantas, kosekantas

Atvirkštinės funkcijos

Atvirkštinės sinuso ir kosinuso funkcijos yra atitinkamai arcsinusas ir arkosinusas.

Arčinas, arcsin

Arkosinas, arkosas

Nuorodos:
I.N. Bronšteinas, K.A. Semendyaev, Matematikos vadovas inžinieriams ir aukštųjų mokyklų studentams, Lan, 2009 m.