Proprietà del seno e del suo grafico. Proprietà di seno, coseno, tangente e cotangente

In questo articolo, mostreremo come definizioni di seno, coseno, tangente e cotangente di angolo e numero in trigonometria. Qui parleremo di notazione, forniremo esempi di record, forniremo illustrazioni grafiche. In conclusione, tracciamo un parallelo tra le definizioni di seno, coseno, tangente e cotangente in trigonometria e geometria.

Navigazione della pagina.

Definizione di seno, coseno, tangente e cotangente

Seguiamo come si forma il concetto di seno, coseno, tangente e cotangente nel corso di matematica della scuola. Nelle lezioni di geometria viene data la definizione di seno, coseno, tangente e cotangente di un angolo acuto in un triangolo rettangolo. E successivamente si studia la trigonometria, che si riferisce al seno, coseno, tangente e cotangente dell'angolo di rotazione e del numero. Diamo tutte queste definizioni, diamo esempi e diamo i commenti necessari.

Angolo acuto in un triangolo rettangolo

Dal corso della geometria sono note le definizioni di seno, coseno, tangente e cotangente di un angolo acuto in un triangolo rettangolo. Sono dati come rapporto tra i lati di un triangolo rettangolo. Vi presentiamo le loro formulazioni.

Definizione.

Seno di un angolo acuto in un triangolo rettangoloè il rapporto tra la gamba opposta e l'ipotenusa.

Definizione.

Coseno di un angolo acuto in un triangolo rettangoloè il rapporto tra la gamba adiacente e l'ipotenusa.

Definizione.

Tangente di un angolo acuto in un triangolo rettangoloè il rapporto tra la gamba opposta e la gamba adiacente.

Definizione.

Cotangente di un angolo acuto in un triangolo rettangoloè il rapporto tra la gamba adiacente e la gamba opposta.

Lì viene introdotta anche la notazione di seno, coseno, tangente e cotangente, rispettivamente sin, cos, tg e ctg.

Ad esempio, se ABC è un triangolo rettangolo con angolo retto C, allora il seno dell'angolo acuto A è uguale al rapporto tra la gamba opposta BC e l'ipotenusa AB, cioè sin∠A=BC/AB.

Queste definizioni consentono di calcolare i valori di seno, coseno, tangente e cotangente di un angolo acuto dalle lunghezze note dei lati di un triangolo rettangolo, nonché dai valori noti di seno, coseno, tangente, cotangente e la lunghezza di uno dei lati, trova le lunghezze degli altri lati. Ad esempio, se sapessimo che in un triangolo rettangolo la gamba AC è 3 e l'ipotenusa AB è 7 , allora potremmo calcolare il coseno dell'angolo acuto A per definizione: cos∠A=AC/AB=3/7 .

Angolo di rotazione

Nella trigonometria, iniziano a guardare l'angolo in modo più ampio: introducono il concetto di angolo di rotazione. L'angolo di rotazione, a differenza di un angolo acuto, non è limitato a fotogrammi da 0 a 90 gradi, l'angolo di rotazione in gradi (e in radianti) può essere espresso da qualsiasi numero reale da −∞ a +∞.

In questa luce, le definizioni di seno, coseno, tangente e cotangente non sono più un angolo acuto, ma un angolo di grandezza arbitraria: l'angolo di rotazione. Sono dati attraverso le coordinate xey del punto A 1 , in cui passa il cosiddetto punto iniziale A(1, 0) dopo aver ruotato di un angolo α attorno al punto O - l'inizio di un sistema di coordinate cartesiane rettangolari e il centro della circonferenza unitaria.

Definizione.

Seno di angolo di rotazioneα è l'ordinata del punto A 1 , cioè sinα=y .

Definizione.

coseno dell'angolo di rotazioneα è detta ascissa del punto A 1 , cioè cosα=x .

Definizione.

Tangente dell'angolo di rotazioneα è il rapporto tra l'ordinata del punto A 1 e la sua ascissa, cioè tgα=y/x .

Definizione.

La cotangente dell'angolo di rotazioneα è il rapporto tra l'ascissa del punto A 1 e la sua ordinata, cioè ctgα=x/y .

Il seno e il coseno sono definiti per qualsiasi angolo α , poiché possiamo sempre determinare l'ascissa e l'ordinata di un punto, che si ottiene ruotando il punto iniziale per l'angolo α . E tangente e cotangente non sono definiti per nessun angolo. La tangente non è definita per tali angoli α in cui il punto iniziale va ad un punto con ascisse zero (0, 1) o (0, −1) , e questo avviene ad angoli 90°+180° k , k∈Z (π /2+π krad). Infatti, a tali angoli di rotazione, l'espressione tgα=y/x non ha senso, poiché contiene una divisione per zero. Per quanto riguarda la cotangente, non è definita per tali angoli α in cui il punto di partenza va a un punto con ordinata zero (1, 0) o (−1, 0) , e questo è il caso per angoli 180° k , k ∈Z (π k rad).

Quindi, seno e coseno sono definiti per qualsiasi angolo di rotazione, la tangente è definita per tutti gli angoli tranne 90°+180° k , k∈Z (π/2+π k rad) e la cotangente è per tutti gli angoli tranne 180 ° ·k , k∈Z (π·k rad).

Le notazioni a noi già note compaiono nelle definizioni sin, cos, tg e ctg, sono usate anche per denotare il seno, coseno, tangente e cotangente dell'angolo di rotazione (a volte si può trovare la notazione tan e cot corrispondente a tangente e cotangente). Quindi il seno dell'angolo di rotazione di 30 gradi può essere scritto come sin30°, i record tg(−24°17′) e ctgα corrispondono alla tangente dell'angolo di rotazione −24 gradi 17 minuti e alla cotangente dell'angolo di rotazione α . Ricordiamo che quando si scrive la misura in radianti di un angolo, la notazione "rad" viene spesso omessa. Ad esempio, il coseno di un angolo di rotazione di tre pi rad è solitamente indicato con cos3 π .

In conclusione di questo paragrafo, vale la pena notare che quando si parla di seno, coseno, tangente e cotangente dell'angolo di rotazione si omette spesso la frase “angolo di rotazione” o la parola “rotazione”. Cioè, invece della frase "seno dell'angolo di rotazione alfa", viene solitamente utilizzata la frase "seno dell'angolo di alfa", o anche più breve - "seno di alfa". Lo stesso vale per coseno, tangente e cotangente.

Diciamo anche che le definizioni di seno, coseno, tangente e cotangente di un angolo acuto in un triangolo rettangolo sono coerenti con le definizioni appena date per seno, coseno, tangente e cotangente di un angolo di rotazione compreso tra 0 e 90 gradi. Lo sosterremo.

Numeri

Definizione.

Seno, coseno, tangente e cotangente di un numero t è un numero uguale rispettivamente a seno, coseno, tangente e cotangente dell'angolo di rotazione in t radianti.

Ad esempio, il coseno di 8 π è, per definizione, un numero uguale al coseno di un angolo di 8 π rad. E il coseno dell'angolo in 8 π rad è uguale a uno, quindi il coseno del numero 8 π è uguale a 1.

C'è un altro approccio alla definizione di seno, coseno, tangente e cotangente di un numero. Consiste nel fatto che ad ogni numero reale t viene assegnato un punto della circonferenza unitaria centrato all'origine del sistema di coordinate rettangolari, e attraverso le coordinate di questo punto si determinano seno, coseno, tangente e cotangente. Soffermiamoci su questo in modo più dettagliato.

Mostriamo come si stabilisce la corrispondenza tra numeri reali e punti della circonferenza:

• al numero 0 viene assegnato il punto di partenza A(1, 0) ;
• un numero positivo t è associato ad un punto della circonferenza unitaria, a cui si arriva se ci muoviamo dal punto di partenza in senso antiorario lungo la circonferenza e percorriamo un percorso di lunghezza t;
• un numero negativo t è associato ad un punto della circonferenza unitaria, a cui si arriva se ci muoviamo dal punto di partenza in senso orario lungo la circonferenza e percorriamo un percorso di lunghezza |t| .

Passiamo ora alle definizioni di seno, coseno, tangente e cotangente del numero t. Assumiamo che il numero t corrisponda ad un punto del cerchio A 1 (x, y) (ad esempio, il numero &pi/2; corrisponde al punto A 1 (0, 1) ).

Definizione.

Il seno di un numero t è l'ordinata del punto della circonferenza unitaria corrispondente al numero t , cioè sint=y .

Definizione.

Il coseno di un numero t è detta ascissa del punto della circonferenza unitaria corrispondente al numero t , cioè cost=x .

Definizione.

Tangente di un numero t è il rapporto tra l'ordinata e l'ascissa del punto della circonferenza unitaria corrispondente al numero t, cioè tgt=y/x. In un'altra formulazione equivalente, la tangente del numero t è il rapporto tra il seno di questo numero e il coseno, cioè tgt=sint/costo .

Definizione.

Cotangente di un numero t è il rapporto tra l'ascissa e l'ordinata del punto della circonferenza unitaria corrispondente al numero t, cioè ctgt=x/y. Un'altra formulazione è la seguente: la tangente del numero t è il rapporto tra il coseno del numero t e il seno del numero t : ctgt=costo/sint .

Qui notiamo che le definizioni appena fornite concordano con la definizione data all'inizio di questa sottosezione. Infatti, il punto della circonferenza unitaria corrispondente al numero t coincide con il punto ottenuto ruotando il punto iniziale di un angolo di t radianti.

Vale anche la pena chiarire questo punto. Diciamo che abbiamo una voce sin3. Come capire se è in questione il seno del numero 3 o il seno dell'angolo di rotazione di 3 radianti? Questo di solito è chiaro dal contesto, altrimenti probabilmente non ha importanza.

Funzioni trigonometriche di argomento angolare e numerico

Secondo le definizioni date nel paragrafo precedente, ad ogni angolo di rotazione α corrisponde un valore ben definito sin α , nonché il valore cos α . Inoltre, tutti gli angoli di rotazione diversi da 90°+180° k , k∈Z (π/2+π k rad) corrispondono ai valori tgα , e diversi da 180° k , k∈Z (π k rad ) sono i valori di ctga. Quindi sinα, cosα, tga e ctga sono funzioni dell'angolo α. In altre parole, queste sono funzioni dell'argomento angolare.

Allo stesso modo, possiamo parlare delle funzioni seno, coseno, tangente e cotangente di un argomento numerico. Ad ogni numero reale t corrisponde infatti un valore ben definito di sint , oltre che di costo . Inoltre, tutti i numeri diversi da π/2+π·k , k∈Z corrispondono ai valori tgt e i numeri π·k , k∈Z corrispondono ai valori ctgt .

Vengono chiamate le funzioni seno, coseno, tangente e cotangente funzioni trigonometriche di base.

Di solito è chiaro dal contesto che si tratta di funzioni trigonometriche di un argomento angolare o di un argomento numerico. Altrimenti, possiamo considerare la variabile indipendente sia come una misura dell'angolo (l'argomento dell'angolo) che come un argomento numerico.

Tuttavia, la scuola studia principalmente le funzioni numeriche, cioè le funzioni i cui argomenti, così come i loro corrispondenti valori di funzione, sono numeri. Pertanto, se stiamo parlando di funzioni, è consigliabile considerare le funzioni trigonometriche come funzioni di argomenti numerici.

Collegamento di definizioni da geometria e trigonometria

Se consideriamo l'angolo di rotazione α da 0 a 90 gradi, i dati nel contesto della trigonometria della definizione di seno, coseno, tangente e cotangente dell'angolo di rotazione sono pienamente coerenti con le definizioni di seno, coseno , tangenti e cotangenti di un angolo acuto in un triangolo rettangolo, che sono date nel corso di geometria. Confermiamo questo.

Disegna un cerchio unitario nel sistema di coordinate cartesiane rettangolari Oxy. Notare il punto di partenza A(1, 0) . Ruotiamolo di un angolo α compreso tra 0 e 90 gradi, otteniamo il punto A 1 (x, y) . Lasciamo cadere la perpendicolare A 1 H dal punto A 1 all'asse Ox.

È facile vedere che in un triangolo rettangolo l'angolo A 1 OH è uguale all'angolo di rotazione α, la lunghezza della gamba OH adiacente a tale angolo è uguale all'ascissa del punto A 1, cioè |OH |=x, la lunghezza della gamba A 1 H opposta all'angolo è uguale all'ordinata del punto A 1 , cioè |A 1 H|=y , e la lunghezza dell'ipotenusa OA 1 è uguale a uno , poiché è il raggio della circonferenza unitaria. Quindi, per definizione dalla geometria, il seno di un angolo acuto α in un triangolo rettangolo A 1 OH è uguale al rapporto tra la gamba opposta e l'ipotenusa, cioè sinα=|A 1 H|/|OA 1 |= y/1=y . E per definizione dalla trigonometria, il seno dell'angolo di rotazione α è uguale all'ordinata del punto A 1, cioè sinα=y. Ciò dimostra che la definizione del seno di un angolo acuto in un triangolo rettangolo è equivalente alla definizione del seno dell'angolo di rotazione α per α da 0 a 90 gradi.

Allo stesso modo, si può dimostrare che le definizioni di coseno, tangente e cotangente di un angolo acuto α sono coerenti con le definizioni di coseno, tangente e cotangente dell'angolo di rotazione α.

Bibliografia.

1. Geometria. 7-9 gradi: studi. per l'istruzione generale istituzioni / [L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev e altri]. - 20a ed. M.: Educazione, 2010. - 384 p.: ill. - ISBN 978-5-09-023915-8.
2. Pogorelov AV Geometria: proc. per 7-9 cellule. educazione generale istituzioni / A. V. Pogorelov. - 2a ed. - M.: Illuminismo, 2001. - 224 p.: ill. - ISBN 5-09-010803-X.
3. Algebra e funzioni elementari: Libro di testo per studenti di grado 9 della scuola secondaria / E. S. Kochetkov, E. S. Kochetkova; A cura del Dottore in Scienze Fisiche e Matematiche O. N. Golovin - 4a ed. Mosca: Istruzione, 1969.
4. Algebra: Proc. per 9 celle. media scuola / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; ed. SA Telyakovsky.- M.: Illuminismo, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
5. Algebra e l'inizio dell'analisi: Proc. per 10-11 cellule. educazione generale istituzioni / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn e altri; ed. A. N. Kolmogorova.- 14a ed.- M.: Enlightenment, 2004.- 384 p.: ill.- ISBN 5-09-013651-3.
6. Mordkovich A.G. L'algebra e gli inizi dell'analisi. Grado 10. Alle 14 Parte 1: un libro di testo per le istituzioni educative (livello di profilo) / A. G. Mordkovich, P. V. Semenov. - 4a ed., aggiungere. - M.: Mnemosyne, 2007. - 424 p.: ill. ISBN 978-5-346-00792-0.
7. Algebra e l'inizio dell'analisi matematica. Grado 10: libro di testo. per l'istruzione generale istituzioni: base e profilo. livelli /[Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; ed. AB Zhizhchenko. - 3a ed. - I.: Istruzione, 2010. - 368 p.: Ill. - ISBN 978-5-09-022771-1.
8. Bashmakov MI L'algebra e l'inizio dell'analisi: Proc. per 10-11 cellule. media scuola - 3a ed. - M.: Illuminismo, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
9. Gusev V.A., Mordkovich A.G. Matematica (un manuale per i candidati alle scuole tecniche): Proc. indennità.- M.; Più alto scuola, 1984.-351 p., ill.

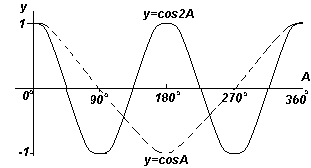
Si può notare dai grafici che:

1. I grafici seno e coseno oscillano tra -1 e 1
2. La curva del coseno ha la stessa forma della curva del seno, ma è spostata rispetto ad essa di 90°
3. Le curve seno e coseno sono continue e si ripetono con un periodo di 360°, la curva tangente ha discontinuità e si ripete con un periodo di 180°.

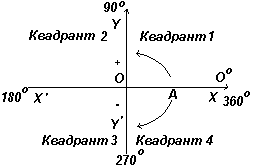Sulla fig. a sinistra sono mostrati gli assi perpendicolari XX" e YY"; intersecante all'origine O. Quando si lavora con i grafici, le misurazioni a destra e in alto da O sono considerate positive, a sinistra e in basso da O - negativo. Lascia che l'OA ruoti liberamente rispetto a O. Quando l'OA viene ruotato in senso antiorario, l'angolo misurato è considerato positivo e quando viene ruotato in senso orario è negativo.

Programma. positivo o negativo
direzione in moto circolare.

Lascia che OA ruoti in senso antiorario in modo tale che Θ 1 sia un angolo qualsiasi nel primo quadrante e costruisci una perpendicolare AB per ottenere un triangolo rettangolo OAB in fig. sinistra. Poiché tutti e tre i lati del triangolo sono positivi, le funzioni trigonometriche seno, coseno e tangente nel primo quadrante saranno positive. (Si noti che la lunghezza di OA è sempre positiva perché è il raggio del cerchio.)
Lascia che OA ruoti ulteriormente in modo tale che Θ 2 sia un angolo qualsiasi nel secondo quadrante e costruisci l'AC in modo che si formi un triangolo rettangolo OAC. Allora sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Lascia che OA ruoti ulteriormente in modo tale che Θ 3 sia un angolo qualsiasi nel terzo quadrante e costruisci AD in modo da formare un triangolo rettangolo OAD. Allora sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

Programma. Costruire angoli
vari quadranti.

Lascia che OA ruoti ulteriormente in modo tale che Θ 4 sia un angolo qualsiasi nel quarto quadrante e costruisci AE in modo che si formi un triangolo rettangolo OAE. Allora sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

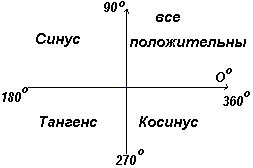
Nel primo quadrante tutte le funzioni trigonometriche hanno valori positivi, nel secondo solo il seno è positivo, nel terzo solo la tangente, nel quarto solo il coseno, che è mostrato in Fig. sinistra.

La conoscenza degli angoli di grandezza arbitraria è necessaria quando si trovano, ad esempio, tutti gli angoli compresi tra 0 o e 360 ​​o il cui seno è, diciamo, 0,3261. Se inserisci 0.3261 nella calcolatrice e premi il pulsante sin -1, otteniamo la risposta 19.03 o. Tuttavia, esiste un secondo angolo compreso tra 0 o e 360 ​​o che la calcolatrice non mostrerà. Il seno è positivo anche nel secondo quadrante. L'altro angolo è mostrato in Fig. sotto come angolo Θ, dove Θ=180 o - 19,03 o = 160,97 o . Pertanto, 19,03 o e 160,97 o sono angoli nell'intervallo da 0 o a 360 o il cui seno è 0,3261.

Stai attento! La calcolatrice fornisce solo uno di questi valori. Il secondo valore dovrebbe essere determinato secondo la teoria degli angoli di grandezza arbitraria.

Esempio 1

Trova tutti gli angoli compresi tra 0 o e 360 ​​o il cui seno è -0,7071

Soluzione:
Gli angoli il cui seno è -0,7071 o sono nel terzo e nel quarto quadrante perché il seno è negativo in quei quadranti (vedi figura a sinistra).

Programma. Trovare tutti gli angoli di
dato valore seno (esempio)

Dalla figura seguente Θ = arcsin 0,7071 = 45 o . Due angoli nell'intervallo da 0 o a 360 o il cui seno è -0,7071 sono 180 o +45 o \u003d 225 o e 360 ​​o - 45 o \u003d 315 o.

Nota. La calcolatrice fornisce una sola risposta.
Programma. Trovare tutti gli angoli di
dato valore seno (esempio)

Esempio 2

Trova tutti gli angoli compresi tra 0 o e 360 ​​o la cui tangente è 1.327.

Soluzione:
La tangente è positiva nel primo e nel terzo quadrante - fig. sinistra.
Programma. Trovare tutti gli angoli di

Dalla figura sotto Θ = arctan1,327= 53 o .
Due angoli nell'intervallo da 0 o a 360 o la cui tangente è 1.327 sono 53 o e 180 o + 53 o , cioè 233o.
Programma. Trovare tutti gli angoli di
dato valore tangente (esempio)

Sia OR in Fig. a sinistra c'è un vettore di lunghezza unitaria, che ruota liberamente in senso antiorario attorno a O. Un giro produce il cerchio mostrato in fig. e diviso per settori di 15 o . Ogni raggio ha una componente orizzontale e una verticale. Ad esempio, per 30 o la componente verticale è TS e la componente orizzontale è OS.

Dalla definizione di funzioni trigonometriche
sin30 o =TS/TO=TS/1, cioè TS=sin30o e cos30 o =OS/TO=OS/1, cioè OS=cos30o

La componente verticale TS può essere tracciata come T"S", che è uguale al valore corrispondente all'angolo di 30° nel grafico dell'angolo y rispetto a x. Se tutte le componenti verticali, come TS, vengono trasferite al grafico, si otterrà una sinusoide, mostrata in Fig. sopra.

Se tutte le componenti orizzontali, come OS, sono proiettate su un grafico di y vs. x, ottieni un'onda coseno. Queste proiezioni sono facilmente visualizzabili ridisegnando un cerchio con raggio OR e angoli originati dalla verticale, come mostrato nella figura a sinistra.
Dalla fig. a sinistra puoi vedere che la sinusoide ha la stessa forma dell'onda coseno, ma spostata di 90°.

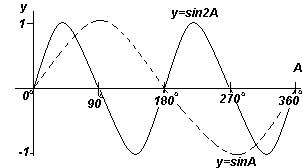Funzioni periodiche e periodo
Ciascuno dei grafici di funzione mostrati nelle quattro Figg. sopra, si ripete all'aumentare dell'angolo A, quindi sono chiamati funzioni periodiche.
Le funzioni y=sinA e y=cosA si ripetono ogni 360 o (o 2π radianti), quindi si chiama 360 o periodo queste funzioni. Le funzioni y=sin2A e y=cos2A si ripetono ogni 180 o (o π radianti), quindi 180 o è il periodo per queste funzioni.
In generale, se y=sinpA e y=cospA (dove p è una costante), allora il periodo della funzione è 360 o /p (o 2π/p radianti). Pertanto, se y=sin3A, il periodo di questa funzione è 360 o /3= 120 o , se y=cos4A, il periodo di questa funzione è 360 o /4= 90 o .

Ampiezza
Ampiezza detto valore massimo della sinusoide. Ciascuno dei grafici 1-4 ha un'ampiezza di +1 (cioè oscillano tra +1 e -1). Tuttavia, se y=4sinA, ciascuno dei valori sinA viene moltiplicato per 4, quindi il valore di ampiezza massima è 4. Allo stesso modo, per y=5cos2A, l'ampiezza è 5 e il periodo è 360 o /2= 180 o .

Esempio 3
Costruisci y=3sin2A nell'intervallo da A= 0 o a A=360 o .

Soluzione:
Ampiezza =3, periodo = 360 o /2 =180 o .

Esempio 4
Traccia y=4cos2x nell'intervallo da x=0 o a x=360 o

Soluzione:
Ampiezza = 4. periodo = 360 o /2 =180 o .

Lag e angoli di attacco
Le curve seno e coseno non iniziano sempre con 0 o . Per tenere conto di questa circostanza, la funzione periodica è rappresentata come y=sin(A± α), dove α è lo sfasamento rispetto a y=sinA e y=cosA.

Dopo aver compilato una tabella di valori, è possibile tracciare la funzione y=sin(A-60 o), mostrata in fig. sinistra. Se la curva y=sinA inizia a 0 o , allora la curva y=sin(A-60 o ) inizia a 60 o (cioè il suo valore zero è 60 o a destra). Quindi, si dice che y=sin(A-60 o) tardi rispetto a y=sinA di 60°.
Programma. y=sin(A-60 o) (onda sinusoidale).

Dopo aver compilato una tabella di valori, è possibile tracciare la funzione y=cos(A+45 o), mostrata in fig. qui di seguito.
Se la curva y=cosA inizia da 0 o , allora la curva y=cos(A+45 o) inizia 45 o a sinistra (cioè il suo valore zero è 45 o prima).
Quindi, il grafico si dice y=cos(A+45 o) davanti a traccia y=cosA a 45°.
Programma. y=cos(A+45 o) (coseno).

In generale, il grafico y=sin(A-α) è in ritardo rispetto a y=sinA di un angolo α.
L'onda coseno ha la stessa forma della sinusoide, ma inizia a 90° a sinistra, cioè davanti a lei di 90 o . Quindi cosA=sin(A+90o).

Esempio 5
Tracciare y=5sin(A+30 o) nell'intervallo da A=0 o a A=360 o

Soluzione:
Ampiezza = 5, periodo = 360 o /1 = 360 o .
5sin(A+30 o) conduce 5sinA di 30 o cioè inizia 30 o prima.
Grafico y=5sin(A+30 o) (sinusoide).

Esempio 6
Tracciare y=7sin(2A-π/3) nell'intervallo da A=0 o a A=360 o .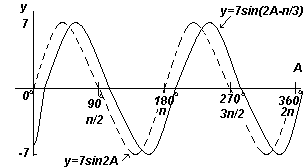

Soluzione:
Ampiezza = 7, periodo = 2π/2= π radianti
Generalmente y=sin(pt-α) è in ritardo rispetto a y=sinpt di α/p, quindi 7sin(2A-π/3) è in ritardo rispetto a 7sin2A di (π/3)/2, cioè per π/6 radianti o 30 o

Sinusoide della forma Asin(ωt±α). angolo di fase. Sfasamento.

Sia OR in fig. a sinistra c'è un vettore che ruota liberamente in senso antiorario attorno a O ad una velocità di ω radianti/s. Viene chiamato il vettore rotante vettore di fase. Dopo un tempo di t secondi, OR ruoterà per l'angolo ωt radianti (nella figura a sinistra, questo è l'angolo TOR). Se ST è costruito perpendicolarmente a OR, allora sinωt=ST/OT, cioè ST=OTsinωt.
Se tutte queste componenti verticali sono proiettate su un grafico di y rispetto a ωt, si otterrà una sinusoide con ampiezza OR.

Se il vettore di fase OR compie un giro (cioè 2π radianti) in T secondi, allora la velocità angolare ω=2π/T rad/s, da cui
Т=2π/ ω (s), dove
T è periodo
Viene chiamato il numero di periodi completi che passano in 1 secondo frequenza F.
Frequenza = (numero di periodi)/(secondi) = 1/ T = ω/2π Hz, quelli. f= ω/2π Hz
Pertanto, la velocità angolare
ω=2πf rad/s.

Se in generale la funzione sinusoidale appare come y=sin(ωt± α), allora
A - ampiezza
ω - velocità angolare
2π/ ω - periodo T, s
ω/2π - frequenza f, Hz
α è l'angolo di anticipo o di ritardo (relativo a y=Аsinωt) in radianti, è anche chiamato angolo di fase.

Esempio 7
La corrente alternata è data come i=20sin(90πt+0,26) ampere. Determina ampiezza, periodo, frequenza e angolo di fase (in gradi)

Soluzione:
i \u003d 20sin (90πt + 0,26) A, quindi,
l'ampiezza è 20 A
velocità angolare ω=90π, quindi,
periodo t= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
frequenza F\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
angolo di fase α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.

Esempio 8
Il meccanismo oscillante ha una cilindrata massima di 3 m e una frequenza di 55 Hz. All'istante t=0 lo spostamento è di 100 cm. Esprimi lo spostamento nella forma generale Аsin(ωt± α).

Soluzione
Ampiezza = spostamento massimo = 3 m
Velocità angolare ω=2πf = 2π(55) = 110 rad/s
Pertanto, lo spostamento è 3sin(110πt + α) m.
A t=0 offset = 100 cm=1 m.
Pertanto, 1= 3sin(0 + α), cioè sinα=1/3=0,33
Quindi α=arcosin0,33=19 o
Quindi l'offset è 3sin(110 πt + 0,33).

Esempio 9
Il valore della tensione istantanea nel circuito AC ad ogni t secondi è dato come v=350sin(40πt-0.542)V. Trovare:
a) Ampiezza, periodo, frequenza e angolo di fase (in gradi)
b) valore di tensione a t = 0
c) valore di tensione a t = 10 ms
d) il tempo necessario affinché la tensione raggiunga per la prima volta i 200 V.
Soluzione:
a) L'ampiezza è 350 V, la velocità angolare è ω=40π
Quindi,
periodo Т=2π/ ω=2π/40π=0,05 s =50ms
frequenza f=1/T=1/0.05=20 Hz
angolo di fase \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o con un ritardo rispetto a v \u003d 350sin (40πt)
b) Se t \u003d 0, allora v \u003d 350sin (0-0,542) \u003d 350sin (-31 o) \u003d -180,25 V
c) Se t \u003d 10 ms, allora v \u003d 350sin (40π10 / 10 3 -0,542) \u003d 350sin (0,714) \u003d 350sin41 o \u003d 229,6 V
d) Se v=200 AND, allora 200=350sin(40πt-0.542) 200/350=sin(40πt-0.542)

Programma. Meccanismo oscillante
(esempio, sinusoide).

v=350sin(40πt-0.542) Pertanto, (40πt-0.542)=arcsin200/350=35 o o 0.611 rad.
40πt= 0,611+0,542=1,153.
Pertanto, se v=200V, allora il tempo t=1.153/40π=9.179 ms

Definizione geometrica di seno e coseno

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α è un angolo espresso in radianti.

Senoè una funzione trigonometrica dell'angolo α tra l'ipotenusa e il cateto di un triangolo rettangolo, uguale al rapporto tra la lunghezza del cateto opposto |BC| alla lunghezza dell'ipotenusa |AB|.

Coseno (cos α)è una funzione trigonometrica dell'angolo α tra l'ipotenusa e il cateto di un triangolo rettangolo, uguale al rapporto tra la lunghezza del cateto adiacente |AC| alla lunghezza dell'ipotenusa |AB|.

Definizione trigonometrica

Usando le formule sopra, puoi trovare il seno e il coseno di un angolo acuto. Ma devi imparare a calcolare il seno e il coseno di un angolo di dimensioni arbitrarie. Un triangolo rettangolo non offre tale opportunità (un angolo ottuso, ad esempio, non può trovarsi al suo interno); pertanto, è necessaria una definizione più generale di seno e coseno, che contenga queste formule come caso speciale.

Il cerchio trigonometrico viene in soccorso. Sia dato un angolo; corrisponde al punto omonimo del cerchio trigonometrico.

Riso. 2. Definizione trigonometrica di seno e coseno

Il coseno di un angolo è l'ascissa di un punto. Il seno di un angolo è l'ordinata di un punto.

Sulla fig. 2 l'angolo è preso acuto, ed è facile comprendere che questa definizione coincide con la definizione geometrica generale. Infatti, vediamo un triangolo rettangolo con un'unità di ipotenusa O e un angolo acuto. La gamba adiacente di questo triangolo è cos (confronta con la Fig. 1) e nello stesso tempo l'ascissa del punto; la gamba opposta è sin (come in Fig. 1) e allo stesso tempo l'ordinata del punto.

Ma ora non siamo più vincolati dal primo trimestre e abbiamo l'opportunità di estendere questa definizione a qualsiasi angolazione. Sulla fig. 3 mostra quali sono il seno e il coseno dell'angolo nel secondo, terzo e quarto quarto.

Riso. 3. Seno e coseno nel II, III e IV quarto

Valori della tabella di seno e coseno

Angolo zero \(\LARGE 0^(\circ ) \)

L'ascissa del punto 0 è 1, l'ordinata del punto 0 è 0. Quindi,

cos 0 = 1 peccato 0 = 0

Fig 4. Angolo zero

Angolo \(\LARGE \frac(\pi)(6) = 30^(\circ ) \)

Vediamo un triangolo rettangolo con un'unità di ipotenusa e un angolo acuto di 30°. Come sapete, la gamba opposta all'angolo 30° è uguale alla metà dell'ipotenusa 1; in altre parole, la gamba verticale è pari a 1/2 e, quindi,

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Troviamo la gamba orizzontale usando il teorema di Pitagora (o, che è lo stesso, troviamo il coseno secondo l'identità trigonometrica principale):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 Perché questo accade? Taglia un triangolo equilatero con il lato 2 lungo la sua altezza! Si divide in due triangoli rettangoli con ipotenusa 2, angolo acuto 30° e gamba più piccola 1.

Fig 5. Angolo π / 6

Angolo \(\LARGE \frac(\pi)(4) = 45^(\circ ) \)

In questo caso, il triangolo rettangolo è isoscele; il seno e il coseno di un angolo di 45° sono uguali tra loro. Indichiamoli con x per ora. Abbiamo:

\[ x^(2) + x^(2) = 1 \]

da cui \(x=\frac(\sqrt(2) )(2) \). Quindi,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Fig 5. Angolo π / 4

Proprietà di seno e coseno

Designazioni accettate

\(\peccato^2 x \equiv (\peccato x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Periodicità

Le funzioni y = sin x e y = cos x sono periodiche con un periodo di 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Parità

La funzione seno è dispari. La funzione coseno è pari.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Domini di definizione e valori, extrema, aumento, diminuzione

Le principali proprietà di seno e coseno sono presentate nella tabella ( n- numero intero).

	\(\piccolo< x < \)	\(\piccolo -\pi + 2\pi n \) \(\piccolo< x < \) \(\small 2\pi n \)
Discendente	\(\piccolo \dfrac(\pi)2 + 2\pi n \)\(\piccolo< x < \) \(\piccolo \dfrac(3\pi)2 + 2\pi n \)	\(\piccolo 2\pi n \) \(\piccolo< x < \) \(\pi + \small 2\pi n \)
Massimi, \(\piccolo x = \) \(\piccolo \dfrac(\pi)2 + 2\pi n \)	\(\piccolo x = 2\pi n\)
Minimo, \(\piccolo x = \) \(\piccolo -\dfrac(\pi)2 + 2\pi n \)	\(\piccolo x = \) \(\piccolo \pi + 2\pi n \)
Zeri, \(\piccolo x = \pi n \)	\(\piccolo x = \dfrac(\pi)2 + \pi n \)
Punti di intersezione con l'asse y, x = 0	y=0	y=1

Formule di base contenenti seno e coseno

Somma dei quadrati

\(\peccato^2 x + \cos^2 x = 1 \)

Formule di somma e differenza di seno e coseno

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \peccato^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Formule per il prodotto di seni e coseni

\(\peccato x \cos y = \) \(\dfrac12 (\Grande [) \sin(x - y) + \sin(x + y) (\Grande ]) \)
\(\peccato x \peccato y = \) \(\dfrac12 (\Grande [) \cos(x - y) - \cos(x + y) (\Grande ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Grande [) \cos(x - y) + \cos(x + y) (\Grande ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Grande [) 1 - \cos 2x (\Grande ]) \)
\(\cos^2 x = \dfrac12 (\Grande [) 1 + \cos 2x (\Grande ]) \)

Formule di somma e differenza

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Espressione da seno a coseno

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\peccato^2 x = 1 - \cos^2 x \) \(\peccato x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\peccato x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Espressione del coseno attraverso il seno

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \peccato^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Espressione in termini di tangente

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

A \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

A \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Tabella di seni e coseni, tangenti e cotangenti

Questa tabella mostra i valori di seno e coseno per alcuni valori dell'argomento.
[ img style="larghezza-max:500px;altezza-max:1080px;" src="tablitsa.png" alt="(!LANG: Tabella di seni e coseni" title="Tabella dei seni e dei coseni" ]!}

Espressioni attraverso variabili complesse

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

formula di Eulero

\(e^(iz) = \cos z + i \sin z \)

Espressioni in termini di funzioni iperboliche

\(\sin iz = io \sh z \) \(\cos iz = \ch z \)
\(\sh iz = io \sin z \) \(\ch iz = \cos z \)

Derivati

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Derivazione di formule > > >

Derivati ​​dell'ennesimo ordine:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Integrali

\(\int \peccato x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Vedi anche la sezione Tabella degli integrali indefiniti >>>

Espansioni in serie

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Secante, cosecante

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

Funzioni inverse

Le funzioni inverse a seno e coseno sono rispettivamente arcoseno e arcocoseno.

Arcseno, arcsino

\(y = \arcsin x \) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

Arcoseno, arccos

\(y = \arccos x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Riferimenti:
IN. Bronstein, KA Semendyaev, Manuale di matematica per ingegneri e studenti di istituti di istruzione superiore, Lan, 2009.

Javascript è disattivato nel tuo browser.
I controlli ActiveX devono essere abilitati per poter fare calcoli!

Centrato nel punto A.
α è l'angolo espresso in radianti.

tangente ( tga) è una funzione trigonometrica dipendente dall'angolo α tra l'ipotenusa e il cateto di un triangolo rettangolo, uguale al rapporto tra la lunghezza del cateto opposto |BC| alla lunghezza del ramo adiacente |AB| .

cotangente ( ctga) è una funzione trigonometrica dipendente dall'angolo α tra l'ipotenusa e il cateto di un triangolo rettangolo, uguale al rapporto tra la lunghezza del cateto adiacente |AB| alla lunghezza della gamba opposta |BC| .

Tangente

Dove n- totale.

Nella letteratura occidentale, la tangente è indicata come segue:
.
;
;
.

Grafico della funzione tangente, y = tg x

Cotangente

Dove n- totale.

Nella letteratura occidentale, la cotangente è indicata come segue:
.
È stata inoltre adottata la seguente notazione:
;
;
.

Grafico della funzione cotangente, y = ctg x

Proprietà di tangente e cotangente

Periodicità

Funzioni y= tg x e y= ctg x sono periodiche con periodo π.

Parità

Le funzioni tangente e cotangente sono dispari.

Domini di definizione e valori, ascendente, discendente

Le funzioni tangente e cotangente sono continue nel loro dominio di definizione (vedi dimostrazione di continuità). Le principali proprietà della tangente e della cotangente sono presentate nella tabella ( n- numero intero).

	y= tg x	y= ctg x
Ambito e continuità
Intervallo di valori	-∞ < y < +∞	-∞ < y < +∞
Ascendente		-
Discendente	-
Estremi	-	-
Zero, y= 0
Punti di intersezione con l'asse y, x = 0	y= 0	-

Formule

Espressioni in termini di seno e coseno

; ;
; ;
;

Formule per tangente e cotangente di somma e differenza

Il resto delle formule sono facili da ottenere, per esempio

Prodotto di tangenti

La formula per la somma e la differenza delle tangenti

Questa tabella mostra i valori di tangenti e cotangenti per alcuni valori dell'argomento.

Espressioni in termini di numeri complessi

Espressioni in termini di funzioni iperboliche

;
;

Derivati

; .

.
Derivata dell'n-esimo ordine rispetto alla variabile x della funzione:
.
Derivazione di formule per tangenti > > > ; per cotangente > > >

Integrali

Espansioni in serie

Per ottenere l'espansione della tangente in potenze di x, devi prendere diversi termini dell'espansione in una serie di potenze per le funzioni peccato x e cos x e dividere questi polinomi l'uno nell'altro, . Ciò si traduce nelle seguenti formule.

A .

in .
dove B n- Numeri di Bernoulli. Sono determinati o dalla relazione di ricorrenza:
;
;
dove .
O secondo la formula di Laplace:

Funzioni inverse

Le funzioni inverse a tangente e cotangente sono rispettivamente arcotangente e arcocotangente.

Arctangente, arct

, dove n- totale.

Arco tangente, arcctg

, dove n- totale.

Riferimenti:
IN. Bronstein, KA Semendyaev, Manuale di matematica per ingegneri e studenti di istituti di istruzione superiore, Lan, 2009.
G. Korn, Manuale di matematica per ricercatori e ingegneri, 2012.

Centrato in un punto UN.
α è un angolo espresso in radianti.

Definizione
Senoè una funzione trigonometrica dipendente dall'angolo α tra l'ipotenusa e il cateto di un triangolo rettangolo, uguale al rapporto tra la lunghezza del cateto opposto |BC| alla lunghezza dell'ipotenusa |AC|.

Coseno (cos α)è una funzione trigonometrica dipendente dall'angolo α tra l'ipotenusa e il cateto di un triangolo rettangolo, uguale al rapporto tra la lunghezza del cateto adiacente |AB| alla lunghezza dell'ipotenusa |AC|.

Designazioni accettate

;
;
.

;
;
.

Grafico della funzione seno, y = sin x

Grafico della funzione coseno, y = cos x

Proprietà di seno e coseno

Periodicità

Funzioni y= peccato x e y= cos x periodico con un punto 2 pi.

Parità

La funzione seno è dispari. La funzione coseno è pari.

Dominio di definizione e valori, extrema, aumento, diminuzione

Le funzioni seno e coseno sono continue nel loro dominio di definizione, cioè per ogni x (vedi la prova di continuità). Le loro proprietà principali sono presentate nella tabella (n - intero).

	y= peccato x	y= cos x
Ambito e continuità	- ∞ < x < + ∞	- ∞ < x < + ∞
Intervallo di valori	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Ascendente
Discendente
Massimi, y= 1
Minimo, y = - 1
Zero, y= 0
Punti di intersezione con l'asse y, x = 0	y= 0	y= 1

Formule di base

Somma di seno e coseno al quadrato

Formule seno e coseno per somma e differenza

;
;

Formule per il prodotto di seni e coseni

Formule di somma e differenza

Espressione da seno a coseno

;
;
;
.

Espressione del coseno attraverso il seno

;
;
;
.

Espressione in termini di tangente

; .

Per , abbiamo:
; .

A :
; .

Tabella di seni e coseni, tangenti e cotangenti

Questa tabella mostra i valori di seno e coseno per alcuni valori dell'argomento.

Espressioni attraverso variabili complesse

;

formula di Eulero

Espressioni in termini di funzioni iperboliche

;
;

Derivati

; . Derivazione di formule > > >

Derivati ​​dell'ennesimo ordine:
{ -∞ < x < +∞ }

Secante, cosecante

Funzioni inverse

Le funzioni inverse a seno e coseno sono rispettivamente arcoseno e arcocoseno.

Arcseno, arcsino

Arcoseno, arccos

Riferimenti:
IN. Bronstein, KA Semendyaev, Manuale di matematica per ingegneri e studenti di istituti di istruzione superiore, Lan, 2009.