Svojstva sinusa i njegovog grafa. Svojstva sinusa, kosinusa, tangenta i kotangensa

U ovom članku ćemo pokazati kako definicije sinusa, kosinusa, tangenta i kotangensa kuta i broja u trigonometriji. Ovdje ćemo govoriti o notaciji, navesti primjere zapisa, dati grafičke ilustracije. Zaključno, povlačimo paralelu između definicija sinusa, kosinusa, tangente i kotangensa u trigonometriji i geometriji.

Navigacija po stranici.

Definicija sinusa, kosinusa, tangenta i kotangensa

Pratimo kako se u školskom kolegiju matematike formira pojam sinusa, kosinusa, tangente i kotangensa. U nastavi geometrije daje se definicija sinusa, kosinusa, tangente i kotangensa oštrog kuta u pravokutnom trokutu. A kasnije se proučava trigonometrija koja se odnosi na sinus, kosinus, tangent i kotangens kuta rotacije i broja. Dajemo sve ove definicije, dajemo primjere i dajemo potrebne komentare.

Oštar kut u pravokutnom trokutu

Iz kolegija geometrije poznate su definicije sinusa, kosinusa, tangente i kotangensa oštrog kuta u pravokutnom trokutu. Oni su dati kao omjer stranica pravokutnog trokuta. Predstavljamo njihove formulacije.

Definicija.

Sinus oštrog kuta u pravokutnom trokutu je omjer suprotnog kraka i hipotenuze.

Definicija.

Kosinus oštrog kuta u pravokutnom trokutu je omjer susjednog kraka i hipotenuze.

Definicija.

Tangenta oštrog kuta u pravokutnom trokutu je omjer suprotne noge i susjedne noge.

Definicija.

Kotangens oštrog kuta u pravokutnom trokutu je omjer susjedne noge i suprotne noge.

Tu se također uvodi oznaka sinusa, kosinusa, tangenta i kotangensa - sin, cos, tg i ctg, redom.

Na primjer, ako je ABC pravokutni trokut s pravim kutom C, tada je sinus oštrog kuta A jednak omjeru suprotnog kraka BC i hipotenuze AB, odnosno sin∠A=BC/AB.

Ove definicije vam omogućuju da izračunate vrijednosti sinusa, kosinusa, tangenta i kotangensa oštrog kuta iz poznatih duljina stranica pravokutnog trokuta, kao i iz poznatih vrijednosti sinusa, kosinusa, tangenta, kotangens i duljina jedne od stranica, pronađite duljine ostalih stranica. Na primjer, kada bismo znali da je u pravokutnom trokutu krak AC 3, a hipotenuza AB 7, tada bismo mogli izračunati kosinus oštrog kuta A po definiciji: cos∠A=AC/AB=3/7.

Kut rotacije

U trigonometriji počinju šire gledati na kut – uvode pojam kuta rotacije. Kut rotacije, za razliku od oštrog kuta, nije ograničen na okvire od 0 do 90 stupnjeva, kut rotacije u stupnjevima (i u radijanima) može se izraziti bilo kojim realnim brojem od −∞ do +∞.

U tom svjetlu, definicije sinusa, kosinusa, tangente i kotangensa više nisu akutni kut, već kut proizvoljne veličine – kut rotacije. Zadane su kroz x i y koordinate točke A 1 , u koju prolazi tzv. početna točka A(1, 0) nakon što se zarotira za kut α oko točke O - početka pravokutnog kartezijanskog koordinatnog sustava i središte jedinične kružnice.

Definicija.

Sinus kuta rotacijeα je ordinata točke A 1 , odnosno sinα=y .

Definicija.

kosinus kuta rotacijeα naziva se apscisa točke A 1 , odnosno cosα=x .

Definicija.

Tangent kuta rotacijeα je omjer ordinate točke A 1 i njezine apscise, odnosno tgα=y/x .

Definicija.

Kotangens kuta rotacijeα je omjer apscise točke A 1 i njezine ordinate, odnosno ctgα=x/y .

Sinus i kosinus su definirani za bilo koji kut α, budući da uvijek možemo odrediti apscisu i ordinatu točke koja se dobiva rotacijom početne točke za kut α. A tangenta i kotangens nisu definirani ni za jedan kut. Tangenta nije definirana za takve kutove α u kojima početna točka ide u točku s nultom apscisom (0, 1) ili (0, −1), a to se događa pod kutovima 90°+180° k , k∈Z (π /2+π k rad). Doista, pri takvim kutovima rotacije, izraz tgα=y/x nema smisla, budući da sadrži dijeljenje s nulom. Što se tiče kotangensa, on nije definiran za takve kutove α kod kojih početna točka ide u točku s nultom ordinatom (1, 0) ili (−1, 0) , a to je slučaj za kutove 180° k , k ∈Z (π k rad).

Dakle, sinus i kosinus su definirani za sve kutove rotacije, tangenta je definirana za sve kutove osim 90°+180° k , k∈Z (π/2+π k rad), a kotangens je za sve kutove osim 180 ° ·k , k∈Z (π·k rad).

Oznake koje su nam već poznate pojavljuju se u definicijama sin, cos, tg i ctg, također se koriste za označavanje sinusa, kosinusa, tangenta i kotangensa kuta rotacije (ponekad možete pronaći zapis tan i cot koji odgovara tangenti i kotangens). Dakle, sinus kuta rotacije od 30 stupnjeva može se zapisati kao sin30°, zapisi tg(−24°17′) i ctgα odgovaraju tangentu kuta rotacije −24 stupnja 17 minuta i kotangensu kuta rotacije α . Podsjetimo da se prilikom pisanja radijanske mjere kuta često izostavlja oznaka "rad". Na primjer, kosinus kuta rotacije od tri pi rada obično se označava cos3 π .

U zaključku ovog odlomka, vrijedno je napomenuti da se u govoru o sinusu, kosinusu, tangentu i kotangensu kuta rotacije često izostavlja izraz "kut rotacije" ili riječ "rotacija". Odnosno, umjesto izraza "sinus kuta rotacije alfa" obično se koristi izraz "sinus kuta alfa", ili još kraće - "sinus alfa". Isto vrijedi i za kosinus, i tangentu i kotangens.

Recimo i da su definicije sinusa, kosinusa, tangenta i kotangensa oštrog kuta u pravokutnom trokutu u skladu s definicijama upravo danim za sinus, kosinus, tangent i kotangens kuta rotacije u rasponu od 0 do 90 stupnjeva. To ćemo potkrijepiti.

Brojevi

Definicija.

Sinus, kosinus, tangent i kotangens broja t je broj jednak sinusu, kosinusu, tangentu i kotangensu kuta rotacije u t radijanima.

Na primjer, kosinus od 8 π je, po definiciji, broj jednak kosinusu kuta od 8 π rad. A kosinus kuta u 8 π rad jednak je jedan, dakle, kosinus broja 8 π jednak je 1.

Postoji još jedan pristup definiciji sinusa, kosinusa, tangenta i kotangensa broja. Sastoji se u tome da je svakom realnom broju t dodijeljena točka jedinične kružnice sa središtem na ishodištu pravokutnog koordinatnog sustava, a sinus, kosinus, tangenta i kotangens određuju se kroz koordinate te točke. Zaustavimo se na ovome detaljnije.

Pokažimo kako se uspostavlja korespondencija između realnih brojeva i točaka kružnice:

• broju 0 ​​dodjeljuje se početna točka A(1, 0) ;
• pozitivan broj t pridružuje se točki na jediničnoj kružnici, do koje ćemo doći ako se krećemo oko kružnice od početne točke u smjeru suprotnom od kazaljke na satu i prođemo put duljine t;
• negativan broj t pridružuje se točki na jediničnoj kružnici, do koje ćemo doći ako se pomičemo po kružnici od početne točke u smjeru kazaljke na satu i prođemo put duljine |t| .

Prijeđimo sada na definicije sinusa, kosinusa, tangenta i kotangensa broja t. Pretpostavimo da broj t odgovara točki kružnice A 1 (x, y) (na primjer, broj &pi/2; odgovara točki A 1 (0, 1) ).

Definicija.

Sinus broja t je ordinata točke jedinične kružnice koja odgovara broju t, odnosno sint=y.

Definicija.

Kosinus broja t se naziva apscisa točke jedinične kružnice koja odgovara broju t, odnosno trošak=x.

Definicija.

Tangent broja t je omjer ordinate i apscise točke jedinične kružnice koja odgovara broju t, odnosno tgt=y/x. U drugoj ekvivalentnoj formulaciji, tangent broja t je omjer sinusa ovog broja i kosinusa, to jest, tgt=sint/cost .

Definicija.

Kotangens broja t je omjer apscise i ordinate točke jedinične kružnice koja odgovara broju t, odnosno ctgt=x/y. Druga formulacija je sljedeća: tangent broja t je omjer kosinusa broja t i sinusa broja t : ctgt=cost/sint .

Ovdje napominjemo da se upravo navedene definicije slažu s definicijom danom na početku ovog pododjeljka. Doista, točka jedinične kružnice koja odgovara broju t podudara se s točkom dobivenom rotacijom početne točke kroz kut od t radijana.

Također je vrijedno pojasniti ovu točku. Recimo da imamo sin3 unos. Kako razumjeti je li u pitanju sinus broja 3 ili sinus kuta rotacije od 3 radijana? To je obično jasno iz konteksta, inače vjerojatno nije važno.

Trigonometrijske funkcije kutnog i numeričkog argumenta

Prema definicijama danim u prethodnom paragrafu, svakom kutu rotacije α odgovara dobro definirana vrijednost sin α , kao i vrijednost cos α . Osim toga, svi kutovi rotacije osim 90°+180° k, k∈Z (π/2+π k rad) odgovaraju vrijednostima tgα, a osim 180° k, k∈Z (π k rad) su vrijednosti ctgα . Stoga su sinα, cosα, tgα i ctgα funkcije kuta α. Drugim riječima, to su funkcije kutnog argumenta.

Slično, možemo govoriti o funkcijama sinus, kosinus, tangent i kotangens numeričkog argumenta. Doista, svaki realni broj t odgovara dobro definiranoj vrijednosti sint , kao i trošku . Osim toga, svi brojevi osim π/2+π·k, k∈Z odgovaraju vrijednostima tgt, a brojevi π·k, k∈Z odgovaraju vrijednostima ctgt.

Funkcije sinus, kosinus, tangent i kotangens se nazivaju osnovne trigonometrijske funkcije.

Obično je iz konteksta jasno da imamo posla s trigonometrijskim funkcijama kutnog argumenta ili numeričkog argumenta. Inače, nezavisnu varijablu možemo smatrati i mjerom kuta (argument kuta) i numeričkim argumentom.

No, škola uglavnom proučava numeričke funkcije, odnosno funkcije čiji su argumenti, kao i odgovarajuće vrijednosti funkcije, brojevi. Stoga, ako govorimo o funkcijama, onda je preporučljivo razmotriti trigonometrijske funkcije kao funkcije brojčanih argumenata.

Povezivanje definicija iz geometrije i trigonometrije

Ako uzmemo u obzir kut rotacije α od 0 do 90 stupnjeva, tada su podaci u kontekstu trigonometrije definicije sinusa, kosinusa, tangenta i kotangensa kuta rotacije u potpunosti u skladu s definicijama sinusa, kosinusa , tangenta i kotangens oštrog kuta u pravokutnom trokutu, koji su dati u tečaju geometrije. Potkrijepimo ovo.

Nacrtajte jediničnu kružnicu u pravokutnom Dekartovom koordinatnom sustavu Oxy. Zabilježite početnu točku A(1, 0) . Zarotirajmo ga za kut α u rasponu od 0 do 90 stupnjeva, dobit ćemo točku A 1 (x, y) . Ispustimo okomicu A 1 H iz točke A 1 na os Ox.

Lako je vidjeti da je u pravokutnom trokutu kut A 1 OH jednak kutu rotacije α, duljina kraka OH koja je susjedna ovom kutu jednaka je apscisi točke A 1, odnosno |OH | |=x, duljina kraka A 1 H nasuprot kuta jednaka je ordinati točke A 1 , odnosno |A 1 H|=y , a duljina hipotenuze OA 1 jednaka je jedan , budući da je to polumjer jedinične kružnice. Tada je, prema definiciji iz geometrije, sinus oštrog kuta α u pravokutnom trokutu A 1 OH jednak omjeru suprotne katete i hipotenuze, odnosno sinα=|A 1 H|/|OA 1 |= y/1=y . A po definiciji iz trigonometrije, sinus kuta rotacije α jednak je ordinati točke A 1, odnosno sinα=y. To pokazuje da je definicija sinusa oštrog kuta u pravokutnom trokutu ekvivalentna definiciji sinusa kuta rotacije α za α od 0 do 90 stupnjeva.

Slično, može se pokazati da su definicije kosinusa, tangenta i kotangensa oštrog kuta α u skladu s definicijama kosinusa, tangenta i kotangensa kuta rotacije α.

Bibliografija.

1. Geometrija. 7-9 razreda: studije. za opće obrazovanje institucije / [L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev i drugi]. - 20. izd. M.: Obrazovanje, 2010. - 384 str.: ilustr. - ISBN 978-5-09-023915-8.
2. Pogorelov A.V. Geometrija: Proc. za 7-9 ćelija. opće obrazovanje ustanove / A. V. Pogorelov. - 2. izd. - M.: Prosvjeta, 2001. - 224 str.: ilustr. - ISBN 5-09-010803-X.
3. Algebra i elementarne funkcije: Udžbenik za učenike 9. razreda srednje škole / E. S. Kochetkov, E. S. Kochetkova; Uredio doktor fizikalno-matematičkih znanosti O. N. Golovin - 4. izd. Moskva: Prosveta, 1969.
4. Algebra: Proc. za 9 ćelija. prosječno škola / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Prosvjeta, 1990.- 272 str.: Ill.- ISBN 5-09-002727-7
5. Algebra i početak analize: Proc. za 10-11 ćelija. opće obrazovanje institucije / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn i drugi; Ed. A. N. Kolmogorova.- 14. izd.- M.: Prosvjeta, 2004.- 384 str.: ilustr.- ISBN 5-09-013651-3.
6. Mordkovich A. G. Algebra i počeci analize. 10. razred. U 14 sati 1. dio: udžbenik za obrazovne ustanove (profilna razina) / A. G. Mordkovich, P. V. Semenov. - 4. izd., dodaj. - M.: Mnemosyne, 2007. - 424 str.: ilustr. ISBN 978-5-346-00792-0.
7. Algebra i početak matematičke analize. 10. razred: udžbenik. za opće obrazovanje ustanove: osnovne i profilne. razine /[Yu. M. Koljagin, M. V. Tkačeva, N. E. Fedorova, M. I. Šabunjin]; izd. A. B. Zhizhchenko. - 3. izd. - I .: Prosvjeta, 2010. - 368 str.: Ill. - ISBN 978-5-09-022771-1.
8. Bašmakov M.I. Algebra i početak analize: Zbornik. za 10-11 ćelija. prosječno škola - 3. izd. - M.: Prosvjeta, 1993. - 351 str.: ilustr. - ISBN 5-09-004617-4.
9. Gusev V. A., Mordkovich A. G. Matematika (priručnik za pristupnike tehničkih škola): Proc. dodatak.- M.; Viša škola, 1984.-351 str., ilustr.

Iz grafikona se može vidjeti da:

1. Sinusni i kosinusni grafikoni fluktuiraju između -1 i 1
2. Kosinusna krivulja ima isti oblik kao i sinusna krivulja, ali je pomaknuta u odnosu na nju za 90 o
3. Sinusne i kosinusne krivulje su kontinuirane i ponavljaju se s periodom od 360 o, tangentna krivulja ima diskontinuitete i ponavlja se s periodom od 180 o.

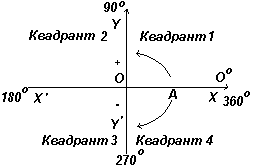Na sl. lijevo su prikazane okomite osi XX" i YY"; sijeku se u ishodištu O. Kod rada s grafovima mjerenja desno i gore od O smatraju se pozitivnim, lijevo i dolje od O - negativnim. Neka OA rotira slobodno u odnosu na O. Kada se OA okrene suprotno od kazaljke na satu, izmjereni kut se smatra pozitivnim, a kada se okrene u smjeru kazaljke na satu, negativan je.

Raspored. pozitivno ili negativno
smjer u kružnom kretanju.

Neka OA rotira u smjeru suprotnom od kazaljke na satu na način da je Θ 1 bilo koji kut u prvom kvadrantu i konstruirajte okomitu AB kako biste dobili pravokutni trokut OAB na sl. lijevo. Budući da su sve tri strane trokuta pozitivne, trigonometrijske funkcije sinus, kosinus i tangenta u prvom kvadrantu bit će pozitivne. (Imajte na umu da je duljina OA uvijek pozitivna jer je to polumjer kružnice.)
Neka OA rotira dalje na način da je Θ 2 bilo koji kut u drugom kvadrantu i konstruirajte AC tako da nastane pravokutni trokut OAC. Tada sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Neka OA rotira dalje na način da je Θ 3 bilo koji kut u trećem kvadrantu i konstruirajte AD tako da nastane pravokutni trokut OAD. Tada je sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

Raspored. Izgradnja kutova u
raznim kvadrantima.

Neka OA rotira dalje na način da je Θ 4 bilo koji kut u četvrtom kvadrantu i konstruirajte AE tako da nastane pravokutni trokut OAE. Tada je sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

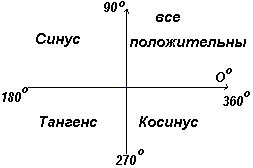
U prvom kvadrantu sve trigonometrijske funkcije imaju pozitivne vrijednosti, u drugom je pozitivan samo sinus, u trećem samo tangenta, u četvrtom samo kosinus, što je prikazano na sl. lijevo.

Poznavanje kutova proizvoljne veličine potrebno je pri pronalaženju, na primjer, svih kutova između 0 o i 360 o čiji je sinus, recimo, 0,3261. Ako u kalkulator unesete 0,3261 i pritisnete tipku sin -1, dobit ćemo odgovor 19.03 o. Međutim, postoji drugi kut između 0 o i 360 o koji kalkulator neće prikazati. Sinus je također pozitivan u drugom kvadrantu. Drugi kut je prikazan na sl. ispod kao kut Θ, gdje je Θ=180 o - 19,03 o = 160,97 o . Dakle, 19,03 o i 160,97 o su kutovi u rasponu od 0 o do 360 o čiji je sinus 0,3261.

Budi oprezan! Kalkulator daje samo jednu od ovih vrijednosti. Drugu vrijednost treba odrediti prema teoriji kutova proizvoljne veličine.

Primjer 1

Pronađite sve kutove između 0 o i 360 o čiji je sinus -0,7071

Riješenje:
Kutovi čiji je sinus -0,7071 o nalaze se u trećem i četvrtom kvadrantu jer je sinus negativan u tim kvadrantima (vidi sliku lijevo).

Raspored. Pronalaženje svih kutova po
zadana vrijednost sinusa (primjer)

Sa sljedeće slike Θ = arcsin 0,7071 = 45 o . Dva kuta u rasponu od 0 o do 360 o čiji je sinus -0,7071 su 180 o +45 o \u003d 225 o i 360 o - 45 o \u003d 315 o.

Bilješka. Kalkulator daje samo jedan odgovor.
Raspored. Pronalaženje svih kutova po
zadana vrijednost sinusa (primjer)

Primjer 2

Pronađite sve kutove između 0 o i 360 o čija je tangenta 1,327.

Riješenje:
Tangenta je pozitivna u prvom i trećem kvadrantu - sl. lijevo.
Raspored. Pronalaženje svih kutova po

Sa donje slike Θ = arctan1,327= 53 o .
Dva kuta u rasponu od 0 o do 360 o čiji je tangent 1,327 su 53 o i 180 o + 53 o , t.j. 233o.
Raspored. Pronalaženje svih kutova po
zadana vrijednost tangente (primjer)

Neka ILI na sl. s lijeve strane je vektor jedinične duljine, koji se slobodno okreće u smjeru suprotnom od kazaljke na satu oko O. Jedan okret stvara krug prikazan na sl. i podijeljena po sektorima od 15 o . Svaki radijus ima horizontalnu i vertikalnu komponentu. Na primjer, za 30 o vertikalna komponenta je TS, a horizontalna komponenta OS.

Iz definicije trigonometrijskih funkcija
sin30 o =TS/TO=TS/1, tj. TS=sin30o i cos30 o =OS/TO=OS/1, tj. OS=cos30o

Vertikalna komponenta TS može se nacrtati kao T"S", što je jednako vrijednosti koja odgovara kutu od 30° na dijagramu kuta y naspram x. Ako se sve vertikalne komponente, poput TS, prenesu na graf, tada će se dobiti sinusoida, prikazana na sl. iznad.

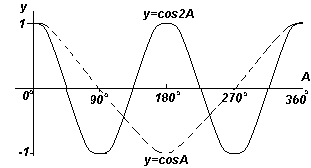
Ako se sve horizontalne komponente, poput OS, projiciraju na dijagram y vs. x, dobit ćete kosinusni val. Ove je projekcije lako vizualizirati ponovnim crtanjem kruga s polumjerom OR i kutovima koji potječu od vertikale, kao što je prikazano na slici lijevo.
Od sl. na lijevoj strani možete vidjeti da sinusoida ima isti oblik kao kosinusni val, ali pomaknut za 90o.

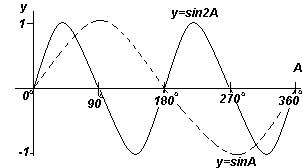Periodične funkcije i period
Svaki od grafova funkcija prikazanih na četiri Sl. gore, ponavlja se kako se kut A povećava, pa se nazivaju periodične funkcije.
Funkcije y=sinA i y=cosA ponavljaju se svakih 360 o (ili 2π radijana), pa se 360 ​​o naziva razdoblje ove funkcije. Funkcije y=sin2A i y=cos2A ponavljaju se svakih 180 o (ili π radijana), tako da je 180 o razdoblje za ove funkcije.
Općenito, ako je y=sinpA i y=cospA (gdje je p konstanta), tada je period funkcije 360 ​​o /p (ili 2π/p radijana). Stoga, ako je y=sin3A, tada je period ove funkcije 360 ​​o /3= 120 o , ako je y=cos4A, tada je period ove funkcije 360 ​​o /4= 90 o .

Amplituda
Amplituda naziva maksimalnom vrijednošću sinusoida. Svaki od grafikona 1-4 ima amplitudu od +1 (tj. fluktuira između +1 i -1). Međutim, ako je y=4sinA, svaka od vrijednosti sinA se množi sa 4, tako da je maksimalna vrijednost amplitude 4. Slično, za y=5cos2A, amplituda je 5, a period je 360 ​​o /2= 180 o .

Primjer 3
Izgradite y=3sin2A u rasponu od A= 0 o do A=360 o .

Riješenje:
Amplituda =3, period = 360 o /2 =180 o .

Primjer 4
Nacrtajte y=4cos2x u rasponu od x=0 o do x=360 o

Riješenje:
Amplituda = 4. period = 360 o /2 =180 o .

Lag i vodeći kutovi
Sinusne i kosinusne krivulje ne počinju uvijek od 0 o. Kako bismo uzeli u obzir ovu okolnost, periodična funkcija je predstavljena kao y=sin(A± α), gdje je α fazni pomak u odnosu na y=sinA i y=cosA.

Nakon što ste sastavili tablicu vrijednosti, možete nacrtati funkciju y=sin(A-60 o), prikazanu na sl. lijevo. Ako krivulja y=sinA počinje od 0 o, tada krivulja y=sin(A-60 o) počinje od 60 o (tj. njena nulta vrijednost je 60 o udesno). Dakle, kaže se da je y=sin(A-60 o) kasno u odnosu na y=sinA za 60°.
Raspored. y=sin(A-60 o) (sinusni val).

Nakon što ste sastavili tablicu vrijednosti, možete nacrtati funkciju y=cos(A+45 o), prikazanu na sl. ispod.
Ako krivulja y=cosA počinje od 0 o, tada krivulja y=cos(A+45 o) počinje 45 o ulijevo (tj. njena nulta vrijednost je 45 o ranije).
Dakle, za dijagram se kaže da je y=cos(A+45 o) ispred nečega crta y=cosA na 45°.
Raspored. y=cos(A+45 o) (kosinus).

Općenito, graf y=sin(A-α) zaostaje u odnosu na y=sinA za kut α.
Kosinusni val ima isti oblik kao sinusoida, ali počinje 90 o lijevo, t.j. ispred nje za 90 o . Prema tome, cosA=sin(A+90o).

Primjer 5
Nacrtajte y=5sin(A+30 o) u rasponu od A=0 o do A=360 o

Riješenje:
Amplituda = 5, period = 360 o /1 = 360 o .
5sin(A+30 o) vodi 5sinA za 30 o, tj. počinje 30 sati ranije.
Grafikon y=5sin(A+30 o) (sinusoida).

Primjer 6
Nacrtajte y=7sin(2A-π/3) u rasponu od A=0 o do A=360 o .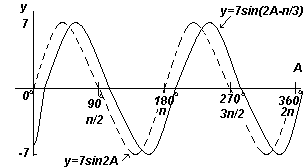

Riješenje:
Amplituda = 7, period = 2π/2= π radijana
Općenito y=sin(pt-α) zaostaje u odnosu na y=sinpt za α/p, dakle 7sin(2A-π/3) kasni u odnosu na 7sin2A za (π/3)/2, tj. po π/6 radijana ili 30 o

Sinusoida oblika Asin(ωt±α). fazni kut. Pomak faze.

Neka ILI na sl. lijevo je vektor koji slobodno rotira u smjeru suprotnom od kazaljke na satu oko O brzinom od ω radiana/s. Rotirajući vektor naziva se fazni vektor. Nakon vremena od t sekundi, OR će se rotirati za kut ωt radijana (na slici lijevo, ovo je kut TOR). Ako je ST konstruiran okomit na OR, tada je sinωt=ST/OT, tj. ST=OTsinωt.
Ako se sve takve okomite komponente projiciraju na dijagram y naspram ωt, dobit će se sinusoida s amplitudom OR.

Ako fazni vektor OR napravi jedan okret (tj. 2π radijana) u T sekundi, tada je kutna brzina ω=2π/T rad/s, odakle
T=2π/ ω (s), gdje je
T je razdoblje
Zove se broj potpunih razdoblja koja prođu u 1 sekundi frekvencija f.
Frekvencija = (broj razdoblja)/(sekunda) = 1/ T = ω/2π Hz, oni. f= ω/2π Hz
Prema tome, kutna brzina
ω=2πf rad/s.

Ako općenito sinusoidna funkcija izgleda kao y=sin(ωt± α), onda
A - amplituda
ω - kutna brzina
2π/ ω - period T, s
ω/2π - frekvencija f, Hz
α je vodeći ili zaostali kut (u odnosu na y=Asinωt) u radijanima, naziva se i fazni kut.

Primjer 7
Izmjenična struja je data kao i=20sin(90πt+0,26) ampera. Odredite amplitudu, period, frekvenciju i fazni kut (u stupnjevima)

Riješenje:
i \u003d 20sin (90πt + 0,26) A, dakle,
amplituda je 20 A
kutna brzina ω=90π, dakle,
razdoblje T= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
frekvencija f\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
fazni kut α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.

Primjer 8
Oscilirajući mehanizam ima maksimalni pomak od 3 m i frekvenciju od 55 Hz. U trenutku t=0 pomak je 100cm. Izrazite pomak u općem obliku Asin(ωt± α).

Riješenje
Amplituda = maksimalni pomak = 3m
Kutna brzina ω=2πf = 2π(55) = 110 rad/s
Prema tome, pomak je 3sin(110πt + α) m.
Kod t=0 pomak = 100cm=1m.
Prema tome, 1= 3sin(0 + α), tj. sinα=1/3=0,33
Stoga je α=arcsin0,33=19 o
Dakle, pomak je 3sin(110 πt + 0,33).

Primjer 9
Vrijednost trenutnog napona u strujnom krugu izmjenične struje u bilo koje t sekundi je data kao v=350sin(40πt-0,542)V. Pronaći:
a) Amplituda, period, frekvencija i fazni kut (u stupnjevima)
b) vrijednost napona pri t = 0
c) vrijednost napona pri t = 10 ms
d) vrijeme potrebno da napon prvi put dosegne 200 V.
Riješenje:
a) Amplituda je 350 V, kutna brzina je ω=40π
Stoga,
period T=2π/ ω=2π/40π=0,05 s =50ms
frekvencija f=1/T=1/0.05=20 Hz
fazni kut \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o s kašnjenjem u odnosu na v = 350sin (40πt)
b) Ako je t = 0, tada v = 350 sin (0-0,542) = 350 sin (-31 o) = -180,25 V
c) Ako je t = 10 ms, tada v = 350sin (40π10 / 10 3 -0,542) = 350sin (0,714) = 350sin41 o = 229,6 V
d) Ako je v=200 I, onda je 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

Raspored. Oscilirajući mehanizam
(primjer, sinusoida).

v=350sin(40πt-0,542) Dakle, (40πt-0,542)=arcsin200/350=35 o ili 0,611 rad.
40πt= 0,611+0,542=1,153.
Stoga, ako je v=200V, tada je vrijeme t=1,153/40π=9,179 ms

Geometrijska definicija sinusa i kosinusa

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α je kut izražen u radijanima.

Sinus je trigonometrijska funkcija kuta α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine suprotnog kraka |BC| na duljinu hipotenuze |AB|.

kosinus (cos α) je trigonometrijska funkcija kuta α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine susjednog kraka |AC| na duljinu hipotenuze |AB|.

Trigonometrijska definicija

Koristeći gornje formule, možete pronaći sinus i kosinus oštrog kuta. Ali morate naučiti kako izračunati sinus i kosinus kuta proizvoljne veličine. Pravokutni trokut ne daje takvu priliku (tupi kut, na primjer, ne može biti u njemu); stoga je potrebna općenitija definicija sinusa i kosinusa, koja sadrži ove formule kao poseban slučaj.

Trigonometrijski krug dolazi u pomoć. Neka je zadan neki kut; odgovara točki istog imena na trigonometrijskoj kružnici.

Riža. 2. Trigonometrijska definicija sinusa i kosinusa

Kosinus kuta je apscisa točke. Sinus kuta je ordinata točke.

Na sl. 2 kut je uzet oštar i lako je razumjeti da se ova definicija podudara s općom geometrijskom definicijom. Doista, vidimo pravokutni trokut s jediničnom hipotenuzom O i oštrim kutom. Susjedni krak ovog trokuta je cos (usporedi sa slikom 1) i istovremeno apscisa točke; suprotni krak je sin (kao na slici 1) i ujedno ordinata točke.

Ali sada više nismo ograničeni prvom četvrtinom i imamo priliku proširiti ovu definiciju na bilo koji kut. Na sl. 3 pokazuje koliki su sinus i kosinus kuta u drugoj, trećoj i četvrtoj četvrtini.

Riža. 3. Sinus i kosinus u II, III i IV četvrtini

Vrijednosti sinusa i kosinusa u tablici

Nulti kut \(\ LARGE 0^(\circ ) \)

Apscisa točke 0 je 1, ordinata točke 0 je 0. Stoga,

cos 0 = 1 sin 0 = 0

Slika 4. Nulti kut

Kut \(\ LARGE \frac(\pi)(6) = 30^(\circ ) \)

Vidimo pravokutni trokut s jediničnom hipotenuzom i oštrim kutom od 30°. Kao što znate, krak nasuprot kuta od 30 ° jednak je polovici hipotenuze 1; drugim riječima, okomita noga je jednaka 1/2 i, prema tome,

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Horizontalnu nogu nalazimo pomoću Pitagorinog teorema (ili, što je isto, nalazimo kosinus prema glavnom trigonometrijskom identitetu):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 Zašto se to događa? Izrežite jednakostranični trokut sa stranom 2 po visini! Raspada se na dva pravokutna trokuta s hipotenuzom 2, oštrim kutom 30° i manjim krakom 1.

Slika 5. Kut π / 6

Kut \(\ LARGE \frac(\pi)(4) = 45^(\circ ) \)

U ovom slučaju, pravokutni trokut je jednakokračan; sinus i kosinus kuta od 45° su međusobno jednaki. Označimo ih za sada s x. Imamo:

\[ x^(2) + x^(2) = 1 \]

odakle \(x=\frac(\sqrt(2) )(2) \). Stoga,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Slika 5. Kut π / 4

Svojstva sinusa i kosinusa

Prihvaćene oznake

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Periodičnost

Funkcije y = sin x i y = cos x su periodične s periodom od 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Paritet

Funkcija sinusa je neparna. Kosinusna funkcija je parna.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Područja definicije i vrijednosti, ekstremi, povećanje, smanjenje

Glavna svojstva sinusa i kosinusa prikazana su u tablici ( n- cijeli broj).

	\(\mali< x < \)	\(\mali -\pi + 2\pi n \) \(\mali< x < \) \(\small 2\pi n \)
Silazni	\(\small \dfrac(\pi)2 + 2\pi n \)\(\mali< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \)	\(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \)
Maksimumi, \(\mali x = \) \(\small \dfrac(\pi)2 + 2\pi n \)	\(\mali x = 2\pi n\)
Minimum, \(\mali x = \) \(\mali -\dfrac(\pi)2 + 2\pi n \)	\(\mali x = \) \(\mali \pi + 2\pi n \)
Nule, \(\mali x = \pi n \)	\(\mali x = \dfrac(\pi)2 + \pi n \)
Točke presjeka s y-osi, x = 0	y=0	y=1

Osnovne formule koje sadrže sinus i kosinus

Zbroj kvadrata

\(\sin^2 x + \cos^2 x = 1 \)

Formule sinusa i kosinusa zbroja i razlike

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \desno) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \desno) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Formule za umnožak sinusa i kosinusa

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large]) \)

Formule zbroja i razlike

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Izraz sinusa kroz kosinus

\(\sin x = \cos\lijevo(\dfrac(\pi)2 - x \desno) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Izraz kosinusa kroz sinus

\(\cos x = \sin\lijevo(\dfrac(\pi)2 - x \desno) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Izraz u terminima tangente

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

Na \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

Na \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Tablica sinusa i kosinusa, tangenta i kotangensa

Ova tablica prikazuje vrijednosti sinusa i kosinusa za neke vrijednosti argumenta.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="(!LANG: Tablica sinusa i kosinusa" title="Tablica sinusa i kosinusa" ]!}

Izrazi kroz kompleksne varijable

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Eulerova formula

\(e^(iz) = \cos z + i \sin z \)

Izrazi u terminima hiperboličkih funkcija

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Derivati

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Izvođenje formula > > >

Derivati ​​n-tog reda:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Integrali

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Vidi također odjeljak Tablica neodređenih integrala >>>

Proširenja u serije

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Sekans, kosekans

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x) \)

Inverzne funkcije

Inverzne funkcije sinusima i kosinusima su arksinus, odnosno arkosinus.

Arcsin, arcsin

\(y = \arcsin x \) \(\lijevo\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \desno\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\lijevo\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \desno\) \)

Arkosinus, arccos

\(y = \arccos x\) \(\lijevo\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \desno\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente visokih učilišta, Lan, 2009.

Javascript je onemogućen u vašem pregledniku.
ActiveX kontrole moraju biti omogućene za izračune!

Centrirano u točki A.
α je kut izražen u radijanima.

tangenta ( tgα) je trigonometrijska funkcija ovisno o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine suprotnog kraka |BC| na duljinu susjedne noge |AB| .

kotangens ( ctgα) je trigonometrijska funkcija ovisno o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine susjednog kraka |AB| na duljinu suprotne noge |BC| .

Tangens

Gdje n- cijeli.

U zapadnoj literaturi tangenta se označava na sljedeći način:
.
;
;
.

Grafikon tangentne funkcije, y = tg x

Kotangens

Gdje n- cijeli.

U zapadnoj literaturi kotangens se označava na sljedeći način:
.
Također je usvojena sljedeća oznaka:
;
;
.

Graf kotangens funkcije, y = ctg x

Svojstva tangente i kotangensa

Periodičnost

Funkcije y= tg x i y= ctg x periodični su s periodom π.

Paritet

Funkcije tangenta i kotangensa su neparne.

Područja definicija i vrijednosti, uzlazno, silazno

Funkcije tangenta i kotangens su kontinuirane u svojoj domeni definicije (vidi dokaz kontinuiteta). Glavna svojstva tangente i kotangensa prikazana su u tablici ( n- cijeli broj).

	y= tg x	y= ctg x
Opseg i kontinuitet
Raspon vrijednosti	-∞ < y < +∞	-∞ < y < +∞
Uzlazni		-
Silazni	-
Ekstremi	-	-
Nule, y= 0
Točke presjeka s y-osi, x = 0	y= 0	-

Formule

Izrazi u terminima sinusa i kosinusa

; ;
; ;
;

Formule za tangente i kotangense zbroja i razlike

Ostale formule lako je dobiti, na primjer

Umnožak tangenti

Formula za zbroj i razliku tangenta

Ova tablica prikazuje vrijednosti tangenta i kotangensa za neke vrijednosti argumenta.

Izrazi u terminima kompleksnih brojeva

Izrazi u terminima hiperboličkih funkcija

;
;

Derivati

; .

.
Derivat n-tog reda s obzirom na varijablu x funkcije:
.
Izvođenje formula za tangentu > > > ; za kotangens > > >

Integrali

Proširenja u serije

Da biste dobili ekspanziju tangente u potencijama x, trebate uzeti nekoliko članova proširenja u nizu potencija za funkcije grijeh x i cos x i podijeliti ove polinome jedan u drugi , . To rezultira sljedećim formulama.

Na .

na .
gdje B n- Bernoullijevi brojevi. One se određuju ili iz relacije ponavljanja:
;
;
gdje .
Ili prema Laplaceovoj formuli:

Inverzne funkcije

Inverzne funkcije tangenti i kotangensu su arktangens, odnosno arkkotangens.

Arktangent, arctg

, gdje n- cijeli.

Arc tangenta, arcctg

, gdje n- cijeli.

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente visokih učilišta, Lan, 2009.
G. Korn, Priručnik za matematiku za istraživače i inženjere, 2012.

Centrirano u točki A.
α je kut izražen u radijanima.

Definicija
Sinus je trigonometrijska funkcija ovisno o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine suprotnog kraka |BC| na duljinu hipotenuze |AC|.

kosinus (cos α) je trigonometrijska funkcija ovisno o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine susjednog kraka |AB| na duljinu hipotenuze |AC|.

Prihvaćene oznake

;
;
.

;
;
.

Grafikon funkcije sinusa, y = sin x

Grafikon kosinusne funkcije, y = cos x

Svojstva sinusa i kosinusa

Periodičnost

Funkcije y= grijeh x i y= cos x periodično s točkom 2 pi.

Paritet

Funkcija sinusa je neparna. Kosinusna funkcija je parna.

Područje definicije i vrijednosti, ekstremi, povećanje, smanjenje

Sinusne i kosinusne funkcije su kontinuirane u svojoj domeni definicije, odnosno za sve x (vidi dokaz kontinuiteta). Njihova glavna svojstva prikazana su u tablici (n - cijeli broj).

	y= grijeh x	y= cos x
Opseg i kontinuitet	- ∞ < x < + ∞	- ∞ < x < + ∞
Raspon vrijednosti	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Uzlazni
Silazni
Maksimumi, y= 1
Minimum, y = - 1
Nule, y= 0
Točke presjeka s y-osi, x = 0	y= 0	y= 1

Osnovne formule

Zbroj kvadrata sinusa i kosinusa

Sinusne i kosinusne formule za zbroj i razliku

;
;

Formule za umnožak sinusa i kosinusa

Formule zbroja i razlike

Izraz sinusa kroz kosinus

;
;
;
.

Izraz kosinusa kroz sinus

;
;
;
.

Izraz u terminima tangente

; .

Za, imamo:
; .

u:
; .

Tablica sinusa i kosinusa, tangenta i kotangensa

Ova tablica prikazuje vrijednosti sinusa i kosinusa za neke vrijednosti argumenta.

Izrazi kroz kompleksne varijable

;

Eulerova formula

Izrazi u terminima hiperboličkih funkcija

;
;

Derivati

; . Izvođenje formula > > >

Derivati ​​n-tog reda:
{ -∞ < x < +∞ }

Sekans, kosekans

Inverzne funkcije

Inverzne funkcije sinusima i kosinusima su arksinus, odnosno arkosinus.

Arcsin, arcsin

Arkosinus, arccos

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente visokih učilišta, Lan, 2009.