साइन और उसके ग्राफ के गुण। साइन, कोसाइन, टेंगेंट और कोटैंजेंट के गुण

05.02.2022

इस लेख में, हम दिखाएंगे कि कैसे त्रिकोणमिति में साइन, कोसाइन, टेंगेंट और कोण और संख्या के कोटेंगेंट की परिभाषाएं. यहां हम अंकन के बारे में बात करेंगे, अभिलेखों के उदाहरण देंगे, ग्राफिक चित्रण देंगे। अंत में, हम त्रिकोणमिति और ज्यामिति में साइन, कोसाइन, स्पर्शरेखा और कोटैंजेंट की परिभाषाओं के बीच एक समानांतर रेखा खींचते हैं।

पृष्ठ नेविगेशन।

साइन, कोसाइन, टेंगेंट और कोटैंजेंट की परिभाषा

आइए देखें कि स्कूल गणित पाठ्यक्रम में साइन, कोसाइन, टेंगेंट और कॉटेंजेंट की अवधारणा कैसे बनती है। ज्यामिति के पाठों में, एक समकोण त्रिभुज में ज्या, कोज्या, स्पर्शरेखा और स्पर्शज्या की परिभाषा दी जाती है। और बाद में त्रिकोणमिति का अध्ययन किया जाता है, जो रोटेशन के कोण और संख्या के साइन, कोसाइन, टेंगेंट और कोटैंजेंट को संदर्भित करता है। हम ये सभी परिभाषाएँ देते हैं, उदाहरण देते हैं और आवश्यक टिप्पणियाँ देते हैं।

समकोण त्रिभुज में न्यून कोण

ज्यामिति के पाठ्यक्रम से, एक समकोण त्रिभुज में एक न्यून कोण की ज्या, कोज्या, स्पर्शरेखा और कोटंगेंट की परिभाषाएँ ज्ञात होती हैं। उन्हें एक समकोण त्रिभुज की भुजाओं के अनुपात के रूप में दिया जाता है। हम उनके सूत्र प्रस्तुत करते हैं।

परिभाषा।

समकोण त्रिभुज में न्यून कोण की ज्याविपरीत पैर का कर्ण से अनुपात है।

परिभाषा।

समकोण त्रिभुज में न्यून कोण की कोज्याआसन्न पैर का कर्ण से अनुपात है।

परिभाषा।

समकोण त्रिभुज में न्यून कोण की स्पर्श रेखाविपरीत पैर का आसन्न पैर से अनुपात है।

परिभाषा।

समकोण त्रिभुज में न्यून कोण का कोटैंजेंटआसन्न पैर का विपरीत पैर का अनुपात है।

साइन, कोसाइन, टेंगेंट और कोटैंजेंट का अंकन भी वहां पेश किया जाता है - क्रमशः पाप, कॉस, टीजी और सीटीजी।

उदाहरण के लिए, यदि ABC समकोण C वाला एक समकोण त्रिभुज है, तो न्यून कोण A की ज्या विपरीत पैर BC और कर्ण AB के अनुपात के बराबर है, अर्थात sin∠A=BC/AB।

ये परिभाषाएँ आपको एक समकोण त्रिभुज की भुजाओं की ज्ञात लंबाई के साथ-साथ साइन, कोसाइन के ज्ञात मानों से एक तीव्र कोण की साइन, कोसाइन, स्पर्शरेखा और कोटेंजेंट के मूल्यों की गणना करने की अनुमति देती हैं। स्पर्शरेखा, कोटैंजेंट और एक भुजा की लंबाई, अन्य भुजाओं की लंबाई ज्ञात कीजिए। उदाहरण के लिए, यदि हम जानते हैं कि एक समकोण त्रिभुज में पैर AC 3 है और कर्ण AB 7 है, तो हम न्यून कोण A की कोज्या की गणना परिभाषा के अनुसार कर सकते हैं: cos∠A=AC/AB=3/7 ।

घूर्णन कोण

त्रिकोणमिति में, वे कोण को अधिक व्यापक रूप से देखना शुरू करते हैं - वे रोटेशन के कोण की अवधारणा का परिचय देते हैं। एक तीव्र कोण के विपरीत, रोटेशन का कोण 0 से 90 डिग्री तक के फ्रेम तक सीमित नहीं है, डिग्री में रोटेशन के कोण (और रेडियन में) को −∞ से +∞ तक किसी भी वास्तविक संख्या द्वारा व्यक्त किया जा सकता है।

इस प्रकाश में, ज्या, कोसाइन, स्पर्शरेखा और कोटांगेंट की परिभाषाएं अब एक न्यून कोण नहीं हैं, बल्कि मनमाने परिमाण का कोण हैं - रोटेशन का कोण। वे बिंदु ए 1 के एक्स और वाई निर्देशांक के माध्यम से दिए गए हैं, जिसमें तथाकथित प्रारंभिक बिंदु ए (1, 0) बिंदु ओ के चारों ओर एक कोण α के माध्यम से घूमने के बाद गुजरता है - एक आयताकार कार्टेशियन समन्वय प्रणाली की शुरुआत और यूनिट सर्कल का केंद्र।

परिभाषा।

घूर्णन कोण की ज्याα बिंदु A 1 की कोटि है, अर्थात sinα=y ।

परिभाषा।

घूर्णन कोण की कोज्याα को बिंदु A 1 का भुज कहा जाता है, अर्थात cosα=x ।

परिभाषा।

घूर्णन कोण की स्पर्शरेखाα, बिंदु A 1 की कोटि का उसके भुज, यानी tgα=y/x से अनुपात है।

परिभाषा।

रोटेशन के कोण का कोटैंजेंटα, बिंदु A 1 के भुज का उसके कोटि से अनुपात है, अर्थात ctgα=x/y ।

साइन और कोसाइन को किसी भी कोण α के लिए परिभाषित किया जाता है, क्योंकि हम हमेशा बिंदु के भुज और कोटि को निर्धारित कर सकते हैं, जो कोण α द्वारा प्रारंभिक बिंदु को घुमाकर प्राप्त किया जाता है। और स्पर्शरेखा और कोटैंजेंट किसी भी कोण के लिए परिभाषित नहीं हैं। स्पर्शरेखा ऐसे कोणों के लिए परिभाषित नहीं है α जिस पर प्रारंभिक बिंदु शून्य भुज (0, 1) या (0, -1) के साथ एक बिंदु पर जाता है, और यह कोणों पर होता है 90°+180° k , k∈Z (π /2+π के रेड)। दरअसल, रोटेशन के ऐसे कोणों पर, अभिव्यक्ति tgα=y/x का कोई मतलब नहीं है, क्योंकि इसमें शून्य से विभाजन होता है। कोटेंजेंट के लिए, यह ऐसे कोणों α के लिए परिभाषित नहीं है, जिस पर प्रारंभिक बिंदु शून्य कोटि (1, 0) या (-1, 0) के साथ एक बिंदु पर जाता है, और यह 180° k , k कोणों के लिए मामला है। Z (π k rad)।

तो, साइन और कोसाइन को किसी भी रोटेशन कोण के लिए परिभाषित किया गया है, स्पर्शरेखा को 90 ° + 180 ° k, k∈Z (π/2+π k rad) को छोड़कर सभी कोणों के लिए परिभाषित किया गया है, और कोटैंजेंट 180 को छोड़कर सभी कोणों के लिए है। ° · k , k∈Z (π·k rad)।

हमारे लिए पहले से ज्ञात संकेतन पाप, कॉस, टीजी और सीटीजी की परिभाषाओं में प्रकट होते हैं, उनका उपयोग रोटेशन के कोण के साइन, कोसाइन, स्पर्शरेखा और कोटेंजेंट को दर्शाने के लिए भी किया जाता है (कभी-कभी आप टैंगेंट के अनुरूप नोटेशन टैन और कोट पा सकते हैं और कोटैंजेंट)। तो 30 डिग्री के रोटेशन कोण की साइन को sin30° के रूप में लिखा जा सकता है, रिकॉर्ड tg(−24°17′) और ctgα रोटेशन कोण −24 डिग्री 17 मिनट के स्पर्शरेखा के अनुरूप होते हैं और रोटेशन कोण α के कोटेंजेंट के अनुरूप होते हैं। . याद रखें कि कोण के रेडियन माप को लिखते समय, अंकन "रेड" को अक्सर छोड़ दिया जाता है। उदाहरण के लिए, तीन पाई रेड के घूर्णन कोण की कोज्या को आमतौर पर cos3 से दर्शाया जाता है।

इस पैराग्राफ के निष्कर्ष में, यह ध्यान देने योग्य है कि रोटेशन के कोण के साइन, कोसाइन, टेंगेंट और कोटेंजेंट के बारे में बात करते समय, वाक्यांश "रोटेशन का कोण" या "रोटेशन" शब्द अक्सर छोड़ा जाता है। यही है, "रोटेशन अल्फा के कोण की साइन" वाक्यांश के बजाय, "अल्फा के कोण की साइन" वाक्यांश आमतौर पर प्रयोग किया जाता है, या इससे भी छोटा - "अल्फा की साइन"। वही कोसाइन, और स्पर्शरेखा, और कोटैंजेंट पर लागू होता है।

आइए यह भी कहें कि एक समकोण त्रिभुज में एक न्यून कोण की साइन, कोसाइन, स्पर्शरेखा और कोटेंजेंट की परिभाषाएं 0 से 90 तक के रोटेशन कोण के साइन, कोसाइन, स्पर्शरेखा और कोटैंजेंट के लिए दी गई परिभाषाओं के अनुरूप हैं। डिग्री। हम इसकी पुष्टि करेंगे।

नंबर

परिभाषा।

किसी संख्या की ज्या, कोज्या, स्पर्शज्या और कोटंगेंट t, t रेडियन में घूर्णन कोण की ज्या, कोज्या, स्पर्शरेखा और कोटैंजेंट के बराबर एक संख्या है।

उदाहरण के लिए, 8 की कोज्या, परिभाषा के अनुसार, 8 रेड के कोण के कोज्या के बराबर एक संख्या है। और 8 रेड में कोण की कोज्या एक के बराबर है, इसलिए संख्या 8 की कोज्या 1 के बराबर है।

किसी संख्या की ज्या, कोज्या, स्पर्शरेखा और कोटंगेंट की परिभाषा के लिए एक और दृष्टिकोण है। यह इस तथ्य में समाहित है कि प्रत्येक वास्तविक संख्या t को आयताकार समन्वय प्रणाली के मूल में केंद्रित इकाई सर्कल का एक बिंदु सौंपा गया है, और साइन, कोसाइन, स्पर्शरेखा और कोटेंजेंट इस बिंदु के निर्देशांक के माध्यम से निर्धारित किए जाते हैं। आइए इस पर अधिक विस्तार से ध्यान दें।

आइए हम दिखाते हैं कि वृत्त की वास्तविक संख्याओं और बिंदुओं के बीच पत्राचार कैसे स्थापित होता है:

संख्या 0 को प्रारंभिक बिंदु A(1, 0) सौंपा गया है;
एक धनात्मक संख्या t इकाई वृत्त पर एक बिंदु के साथ जुड़ा हुआ है, जो हमें तब मिलेगा जब हम वृत्त के चारों ओर प्रारंभिक बिंदु से वामावर्त दिशा में घूमते हैं और लंबाई t के पथ से गुजरते हैं;
एक ऋणात्मक संख्या t इकाई वृत्त पर एक बिंदु के साथ जुड़ा हुआ है, जो हमें तब मिलेगा जब हम वृत्त के चारों ओर प्रारंभिक बिंदु से दक्षिणावर्त दिशा में घूमते हैं और लंबाई के पथ से गुजरते हैं |t| .

आइए अब संख्या t की ज्या, कोज्या, स्पर्शरेखा और कोटंगेंट की परिभाषाओं पर चलते हैं। आइए मान लें कि संख्या टी सर्कल ए 1 (एक्स, वाई) के एक बिंदु से मेल खाती है (उदाहरण के लिए, संख्या &pi/2; बिंदु ए 1 (0, 1) से मेल खाती है)।

परिभाषा।

एक संख्या की ज्या t संख्या t के संगत इकाई वृत्त बिंदु की कोटि है, जो कि sint=y है।

परिभाषा।

एक संख्या की कोज्या t को संख्या t के संगत इकाई वृत्त के बिंदु का भुज कहा जाता है, अर्थात लागत=x।

परिभाषा।

एक संख्या की स्पर्शरेखा t, संख्या t के संगत इकाई वृत्त के बिंदु के भुज से कोटि का अनुपात है, जो कि tgt=y/x है। एक अन्य समकक्ष सूत्रीकरण में, संख्या t की स्पर्शरेखा इस संख्या की ज्या का कोज्या से अनुपात है, जो कि tgt=sint/cost है।

परिभाषा।

किसी संख्या का स्पर्शज्या t संख्या t के संगत इकाई वृत्त के बिंदु की कोटि से भुज का अनुपात है, अर्थात ctgt=x/y. एक अन्य सूत्रीकरण इस प्रकार है: संख्या t की स्पर्शरेखा संख्या t की कोज्या का संख्या t: ctgt=cost/sint की ज्या से अनुपात है।

यहां हम ध्यान दें कि अभी दी गई परिभाषाएं इस उपखंड की शुरुआत में दी गई परिभाषा से मेल खाती हैं। वास्तव में, संख्या t के संगत इकाई वृत्त का बिंदु t रेडियन के कोण के माध्यम से प्रारंभिक बिंदु को घुमाकर प्राप्त बिंदु के साथ मेल खाता है।

इस बिंदु को स्पष्ट करना भी उचित है। मान लें कि हमारे पास sin3 प्रविष्टि है। कैसे समझें कि संख्या 3 की ज्या या 3 रेडियन के घूर्णन कोण की ज्या प्रश्न में है? यह आमतौर पर संदर्भ से स्पष्ट होता है, अन्यथा शायद इससे कोई फर्क नहीं पड़ता।

कोणीय और संख्यात्मक तर्क के त्रिकोणमितीय कार्य

पिछले पैराग्राफ में दी गई परिभाषाओं के अनुसार, प्रत्येक रोटेशन कोण α sinα के एक अच्छी तरह से परिभाषित मान के साथ-साथ cosα के मान से मेल खाता है। इसके अलावा, 90°+180° k , k∈Z (π/2+π k rad) के अलावा सभी रोटेशन कोण tgα और 180° k , k∈Z (π k rad ) के अलावा अन्य मानों के अनुरूप हैं। ctgα के मान हैं। इसलिए sinα, cosα, tgα और ctgα कोण α के कार्य हैं। दूसरे शब्दों में, ये कोणीय तर्क के कार्य हैं।

इसी तरह, हम एक संख्यात्मक तर्क के साइन, कोसाइन, स्पर्शरेखा और कोटेंजेंट के कार्यों के बारे में बात कर सकते हैं। वास्तव में, प्रत्येक वास्तविक संख्या t sint के सुपरिभाषित मान के साथ-साथ लागत से मेल खाती है। इसके अलावा, π/2+π·k , k∈Z के अलावा अन्य सभी संख्याएँ tgt के मान से मेल खाती हैं, और ·k , k∈Z की संख्या ctgt के मानों से मेल खाती है।

साइन, कोसाइन, टेंगेंट और कोटैंजेंट के कार्यों को कहा जाता है बुनियादी त्रिकोणमितीय कार्य.

संदर्भ से यह आमतौर पर स्पष्ट है कि हम कोणीय तर्क या संख्यात्मक तर्क के त्रिकोणमितीय कार्यों के साथ काम कर रहे हैं। अन्यथा, हम स्वतंत्र चर को कोण के माप (कोण तर्क) और संख्यात्मक तर्क दोनों के रूप में मान सकते हैं।

हालांकि, स्कूल मुख्य रूप से संख्यात्मक कार्यों का अध्ययन करता है, यानी ऐसे कार्य जिनके तर्क, साथ ही साथ संबंधित फ़ंक्शन मान संख्याएं हैं। इसलिए, यदि हम कार्यों के बारे में बात कर रहे हैं, तो त्रिकोणमितीय कार्यों को संख्यात्मक तर्कों के कार्यों के रूप में माना जाना उचित है।

ज्यामिति और त्रिकोणमिति से परिभाषाओं का कनेक्शन

यदि हम रोटेशन के कोण α को 0 से 90 डिग्री तक मानते हैं, तो रोटेशन के कोण के साइन, कोसाइन, स्पर्शरेखा और कोटेंजेंट की परिभाषा के त्रिकोणमिति के संदर्भ में डेटा पूरी तरह से साइन, कोसाइन की परिभाषाओं के अनुरूप है। , समकोण त्रिभुज में न्यून कोण की स्पर्श रेखा और कोटेंजेंट, जो ज्यामिति पाठ्यक्रम में दिए गए हैं। आइए इसकी पुष्टि करते हैं।

आयताकार कार्टेशियन निर्देशांक प्रणाली ऑक्सी में एक इकाई वृत्त बनाएं। प्रारंभिक बिंदु A(1, 0) पर ध्यान दें। आइए इसे 0 से 90 डिग्री के कोण α से घुमाएं, हमें बिंदु A 1 (x, y) मिलता है। आइए बिंदु A 1 से ऑक्‍स अक्ष पर लंब A 1 H को छोड़ते हैं।

यह देखना आसान है कि एक समकोण त्रिभुज में कोण A 1 OH घूर्णन कोण α के बराबर होता है, इस कोण से सटे पैर OH की लंबाई बिंदु A 1 के भुज के बराबर होती है, अर्थात |OH |=x, कोण के विपरीत पैर A 1 H की लंबाई बिंदु A 1 की कोटि के बराबर है, अर्थात |A 1 H|=y, और कर्ण OA 1 की लंबाई एक के बराबर है , क्योंकि यह इकाई वृत्त की त्रिज्या है। फिर, ज्यामिति से परिभाषा के अनुसार, एक समकोण त्रिभुज A 1 OH में एक न्यून कोण α की ज्या कर्ण के विपरीत पैर के अनुपात के बराबर होती है, अर्थात sinα=|A 1 H|/|OA 1 |= वाई/1 = वाई। और त्रिकोणमिति से परिभाषा के अनुसार, रोटेशन के कोण की ज्या α बिंदु A 1 की कोटि के बराबर है, जो कि sinα=y है। इससे पता चलता है कि एक समकोण त्रिभुज में न्यून कोण की ज्या की परिभाषा 0 से 90 डिग्री के लिए α के रोटेशन के कोण की साइन की परिभाषा के बराबर है।

इसी तरह, यह दिखाया जा सकता है कि एक न्यून कोण α के कोसाइन, स्पर्शरेखा और कोटैंजेंट की परिभाषाएं रोटेशन के कोण के कोसाइन, स्पर्शरेखा और कोटैंजेंट की परिभाषाओं के अनुरूप हैं।

ग्रंथ सूची।

ज्यामिति। 7-9 ग्रेड: अध्ययन करते हैं। सामान्य शिक्षा के लिए संस्थान / [एल. एस। अतानासियन, वी। एफ। बुटुज़ोव, एस। बी। कदोमत्सेव और अन्य]। - 20 वां संस्करण। एम.: शिक्षा, 2010. - 384 पी .: बीमार। - आईएसबीएन 978-5-09-023915-8।
पोगोरेलोव ए.वी.ज्यामिति: प्रो. 7-9 कोशिकाओं के लिए। सामान्य शिक्षा संस्थान / ए वी पोगोरेलोव। - दूसरा संस्करण। - एम .: ज्ञानोदय, 2001. - 224 पी .: बीमार। - आईएसबीएन 5-09-010803-एक्स।
बीजगणित और प्राथमिक कार्य: माध्यमिक विद्यालय / ई.एस. कोचेतकोव, ई.एस. कोचेतकोवा के ग्रेड 9 के छात्रों के लिए पाठ्यपुस्तक; डॉक्टर ऑफ फिजिकल एंड मैथमैटिकल साइंसेज ओ एन गोलोविन द्वारा संपादित - चौथा संस्करण। मॉस्को: शिक्षा, 1969।
बीजगणित:प्रोक। 9 कोशिकाओं के लिए। औसत स्कूल / यू. एन। मकारिचेव, एन। जी। मिंड्युक, के। आई। नेशकोव, एस। बी। सुवोरोवा; ईडी। एस.ए. तेल्याकोवस्की.- एम.: एनलाइटेनमेंट, 1990.- 272 पी.: बीमार.- आईएसबीएन 5-09-002727-7
बीजगणितऔर विश्लेषण की शुरुआत: प्रोक। 10-11 कोशिकाओं के लिए। सामान्य शिक्षा संस्थान / ए। एन। कोलमोगोरोव, ए। एम। अब्रामोव, यू। पी। डुडनित्सिन और अन्य; ईडी। ए.एन. कोलमोगोरोवा.- 14वां संस्करण.- एम.: एनलाइटेनमेंट, 2004.- 384 पी.: बीमार.- आईएसबीएन 5-09-013651-3।
मोर्दकोविच ए. जी.बीजगणित और विश्लेषण की शुरुआत। ग्रेड 10। दोपहर 2 बजे भाग 1: शैक्षणिक संस्थानों के लिए एक पाठ्यपुस्तक (प्रोफाइल स्तर) / ए। जी। मोर्दकोविच, पी। वी। सेमेनोव। - चौथा संस्करण।, जोड़ें। - एम .: मेनेमोसिन, 2007. - 424 पी .: बीमार। आईएसबीएन 978-5-346-00792-0।
बीजगणितऔर गणितीय विश्लेषण की शुरुआत। ग्रेड 10: पाठ्यपुस्तक। सामान्य शिक्षा के लिए संस्थान: बुनियादी और प्रोफाइल। स्तर / [यू। एम। कोल्यागिन, एम। वी। तकाचेवा, एन। ई। फेडोरोवा, एम। आई। शबुनिन]; ईडी। ए बी झिझचेंको। - तीसरा संस्करण। - मैं।: शिक्षा, 2010। - 368 पी।: बीमार। - आईएसबीएन 978-5-09-022771-1।
बश्माकोव एम.आई.बीजगणित और विश्लेषण की शुरुआत: प्रोक। 10-11 कोशिकाओं के लिए। औसत विद्यालय - तीसरा संस्करण। - एम .: ज्ञानोदय, 1993. - 351 पी .: बीमार। - आईएसबीएन 5-09-004617-4।
गुसेव वी.ए., मोर्दकोविच ए.जी.गणित (तकनीकी स्कूलों के आवेदकों के लिए एक मैनुअल): प्रोक। भत्ता।- एम .; उच्चतर स्कूल, 1984.-351 पी।, बीमार।

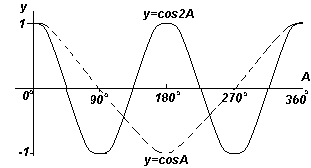
यह रेखांकन से देखा जा सकता है कि:

साइन और कोसाइन प्लॉट -1 और 1 . के बीच उतार-चढ़ाव करते हैं
कोज्या वक्र का आकार ज्या वक्र के समान होता है, लेकिन इसके सापेक्ष 90 o . स्थानांतरित हो जाता है
ज्या और कोज्या वक्र निरंतर हैं और 360 o की अवधि के साथ दोहराए जाते हैं, स्पर्शरेखा वक्र में असंतुलन होता है और 180 o की अवधि के साथ दोहराता है।

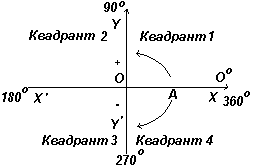अंजीर पर। बाईं ओर लंबवत अक्ष XX" और YY" दिखाए गए हैं; मूल O पर प्रतिच्छेद करना। ग्राफ़ के साथ काम करते समय, O से दाईं और ऊपर की माप को सकारात्मक माना जाता है, बाईं ओर और O से नीचे की ओर - नकारात्मक। ओए के सापेक्ष ओए को स्वतंत्र रूप से घूमने दें। जब ओए को वामावर्त घुमाया जाता है, तो मापा कोण सकारात्मक माना जाता है, और जब दक्षिणावर्त घुमाया जाता है, तो यह नकारात्मक होता है।

अनुसूची। सकारात्मक या नकारात्मक
परिपत्र गति में दिशा।

मान लीजिए OA वामावर्त इस प्रकार घुमाता है कि Θ 1 पहले चतुर्थांश में कोई कोण है, और अंजीर में एक समकोण त्रिभुज OAB प्राप्त करने के लिए एक लंबवत AB की रचना करें। बाएं। चूँकि त्रिभुज की तीनों भुजाएँ धनात्मक हैं, इसलिए पहले चतुर्थांश में त्रिकोणमितीय फलन साइन, कोसाइन और स्पर्शरेखा धनात्मक होंगे। (ध्यान दें कि OA की लंबाई हमेशा धनात्मक होती है क्योंकि यह वृत्त की त्रिज्या होती है।)
OA को आगे इस प्रकार घुमाएँ कि 2 दूसरे चतुर्थांश में कोई कोण हो, और AC की रचना इस प्रकार कीजिए कि एक समकोण त्रिभुज OAC बन जाए। तब पाप 2 =+/+ = +; क्योंकि 2 =+/- = -; टीजी 2 = +/- = -। मान लीजिए OA आगे इस प्रकार घूमता है कि 3 तीसरे चतुर्थांश में कोई कोण है, और AD की रचना कीजिए जिससे एक समकोण त्रिभुज OAD बन जाए। तब पाप 3 = -/+ = -; क्योंकि 3 = -/+ = -; टीजी Θ 3 = -/- =+।

अनुसूची। बिल्डिंग एंगल्स in
विभिन्न चतुर्भुज।

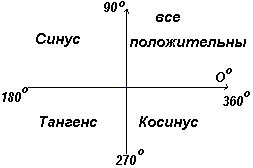मान लीजिए कि OA आगे इस प्रकार घूमता है कि 4 चौथे चतुर्थांश में कोई कोण है, और AE की रचना कीजिए जिससे एक समकोण त्रिभुज OAE बन जाए। तब पाप 4 = -/+= -; क्योंकि 4 =+/+=+; टीजी 4 = -/+= -.

पहले चतुर्थांश में सभी त्रिकोणमितीय फलनों का धनात्मक मान होता है, दूसरे में केवल ज्या धनात्मक होती है, तीसरे में केवल स्पर्शरेखा होती है, चौथे में केवल कोसाइन होती है, जो चित्र में दिखाया गया है। बाएं।

मनमाने परिमाण के कोणों का ज्ञान आवश्यक है, उदाहरण के लिए, 0 o और 360 o के बीच के सभी कोण जिनकी ज्या, मान लीजिए, 0.3261 है। यदि आप कैलकुलेटर में 0.3261 दर्ज करते हैं और पाप -1 बटन दबाते हैं, तो हमें उत्तर 19.03 ओ मिलता है। हालाँकि, 0 o और 360 o के बीच एक दूसरा कोण है जो कैलकुलेटर नहीं दिखाएगा। ज्या द्वितीय चतुर्थांश में भी धनात्मक है। दूसरा कोण अंजीर में दिखाया गया है। कोण Θ के रूप में नीचे, जहां Θ=180 o - 19.03 o = 160.97 o। इस प्रकार, 19.03 o और 160.97 o 0 o से 360 o तक के कोण हैं जिनकी ज्या 0.3261 है।

सावधान रहे! कैलकुलेटर इनमें से केवल एक मान देता है। दूसरा मान मनमाना परिमाण के कोणों के सिद्धांत के अनुसार निर्धारित किया जाना चाहिए।

उदाहरण 1

0 o और 360 o के बीच के सभी कोण ज्ञात कीजिए जिनकी ज्या -0.7071 . है

समाधान:
कोण जिनकी ज्या -0.7071 o है वे तीसरे और चौथे चतुर्थांश में हैं क्योंकि उन चतुर्थांशों में ज्या ऋणात्मक है (बाईं ओर आकृति देखें)।

अनुसूची। द्वारा सभी कोणों का पता लगाना
दिया गया साइन मान (उदाहरण)

निम्नलिखित आकृति से = चाप 0.7071 = 45 o. 0 o से 360 o की सीमा में दो कोण जिनकी ज्या -0.7071 180 o +45 o \u003d 225 o और 360 o - 45 o \u003d 315 o है।

ध्यान दें।कैलकुलेटर केवल एक उत्तर देता है।
अनुसूची। द्वारा सभी कोणों का पता लगाना
दिया गया साइन मान (उदाहरण)

उदाहरण 2

0 o और 360 o के बीच के सभी कोण ज्ञात कीजिए जिनकी स्पर्श रेखा 1.327 है।

समाधान:
पहले और तीसरे चतुर्थांश में स्पर्शरेखा धनात्मक होती है - अंजीर। बाएं।
अनुसूची। द्वारा सभी कोणों का पता लगाना

नीचे दिए गए चित्र से = arctan1,327= 53 o.
0 o से 360 o के परास में दो कोण जिनकी स्पर्श रेखा 1.327 है वे 53 o और 180 o + 53 o हैं, अर्थात्। 233ओ.
अनुसूची। द्वारा सभी कोणों का पता लगाना
दिया गया स्पर्शरेखा मान (उदाहरण)

मान लीजिए या अंजीर में। बाईं ओर इकाई लंबाई का एक वेक्टर है, जो स्वतंत्र रूप से O के चारों ओर वामावर्त घूमता है। एक चक्कर अंजीर में दिखाया गया वृत्त बनाता है। और 15 ओ के क्षेत्रों से विभाजित। प्रत्येक त्रिज्या में एक क्षैतिज और एक ऊर्ध्वाधर घटक होता है। उदाहरण के लिए, 30 o के लिए लंबवत घटक TS है और क्षैतिज घटक OS है।

त्रिकोणमितीय कार्यों की परिभाषा से
sin30 o =TS/TO=TS/1, अर्थात। टीएस = पाप 30oतथा cos30 ओ =ओएस/टीओ=ओएस/1, यानी। ओएस = cos30o

लंबवत घटक टीएस को टी "एस" के रूप में प्लॉट किया जा सकता है, जो कि वाई बनाम एक्स कोण प्लॉट में 30 डिग्री कोण के अनुरूप मान के बराबर है। यदि सभी ऊर्ध्वाधर घटकों, जैसे टीएस, को ग्राफ में स्थानांतरित कर दिया जाता है, तो एक साइनसॉइड प्राप्त होगा, जैसा कि अंजीर में दिखाया गया है। के ऊपर।

यदि सभी क्षैतिज घटकों, जैसे OS, को y बनाम x के प्लॉट पर प्रक्षेपित किया जाता है, तो आपको कोसाइन तरंग प्राप्त होती है। जैसा कि बाईं ओर की आकृति में दिखाया गया है, इन अनुमानों को त्रिज्या OR के साथ एक वृत्त और ऊर्ध्वाधर से उत्पन्न होने वाले कोणों को फिर से बनाकर कल्पना करना आसान है।
अंजीर से। बाईं ओर आप देख सकते हैं कि साइनसॉइड का आकार कोसाइन तरंग के समान है, लेकिन 90 o से स्थानांतरित हो गया है।

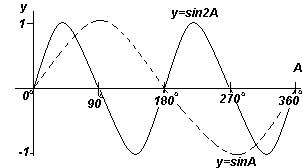आवधिक कार्य और अवधि
चार अंजीर में दिखाए गए प्रत्येक फ़ंक्शन ग्राफ़। ऊपर, कोण A के बढ़ने पर दोहराया जाता है, इसलिए उन्हें कहा जाता है आवधिक कार्य.
फलन y=sinA और y=cosA प्रत्येक 360 o (या 2π रेडियन) दोहराए जाते हैं, इसलिए 360 o कहा जाता है अवधिइन कार्यों। फलन y=sin2A और y=cos2A प्रत्येक 180 o (या रेडियन) दोहराते हैं, इसलिए 180 o इन कार्यों की अवधि है।
सामान्य तौर पर, यदि y=sinpA और y=cospA (जहाँ p एक स्थिरांक है), तो फलन की अवधि 360 o /p (या 2π/p रेडियन) है। इसलिए, यदि y=sin3A, तो इस फलन की अवधि 360 o /3= 120 o है, यदि y=cos4A है, तो इस फलन की अवधि 360 o /4= 90 o है।

आयाम
आयामसाइनसॉइड का अधिकतम मूल्य कहा जाता है। प्रत्येक ग्राफ़ 1-4 में +1 का आयाम होता है (अर्थात वे +1 और -1 के बीच उतार-चढ़ाव करते हैं)। हालाँकि, यदि y=4sinA, प्रत्येक sinA मान को 4 से गुणा किया जाता है, तो अधिकतम आयाम मान 4 है। इसी तरह, y=5cos2A के लिए, आयाम 5 है और अवधि 360 o /2= 180 o है।

उदाहरण 3
y=3sin2A को A= 0 o से A=360 o की सीमा में बनाएं।

समाधान:
आयाम =3, आवर्त = 360 o /2 =180 o ।

उदाहरण 4
प्लॉट y=4cos2x x=0 o से x=360 o . की सीमा में

समाधान:
आयाम = 4. आवर्त = 360 o /2 = 180 o .

अंतराल और सीसा कोण
ज्या और कोज्या वक्र हमेशा 0 o से प्रारंभ नहीं होते हैं। इस परिस्थिति को ध्यान में रखने के लिए, आवधिक कार्य को y=sin(A± α) के रूप में दर्शाया जाता है, जहां α y=sinA और y=cosA के संबंध में चरण बदलाव है।

मूल्यों की एक तालिका संकलित करने के बाद, आप अंजीर में दिखाए गए फ़ंक्शन y=sin(A-60 o) को प्लॉट कर सकते हैं। बाएं। यदि y=sinA वक्र 0 o से प्रारंभ होता है, तो y=sin(A-60 o ) वक्र 60 o से प्रारंभ होता है (अर्थात इसका शून्य मान दाईं ओर 60 o है)। इस प्रकार, यह कहा जाता है कि y=sin(A-60 o) देर y=sinA के सापेक्ष 60°।
अनुसूची। y=sin(A-60 o) (साइन वेव)।

मूल्यों की एक तालिका संकलित करने के बाद, आप अंजीर में दिखाए गए फ़ंक्शन y=cos(A+45 o) को प्लॉट कर सकते हैं। नीचे।
यदि वक्र y=cosA 0 o से प्रारंभ होता है, तो वक्र y=cos(A+45 o) बाईं ओर 45 o प्रारंभ होता है (अर्थात इसका शून्य मान 45 o पहले होता है)।
इस प्रकार, प्लॉट को y=cos(A+45 o) कहा जाता है से आगेप्लॉट y=cosA 45° पर।
अनुसूची। y=cos(A+45 o) (कोज्या)।

सामान्य तौर पर, ग्राफ y=sin(A-α) कोण α से y=sinA के सापेक्ष पिछड़ जाता है।
कोसाइन तरंग का आकार साइनसॉइड के समान होता है, लेकिन 90 o बाईं ओर शुरू होता है, अर्थात। उसके आगे 90 o तक। इसलिए, cosA=sin(A+90o)।

उदाहरण 5
प्लॉट y=5sin(A+30 o) A=0 o से A=360 o की सीमा में

समाधान:
आयाम = 5, आवर्त = 360 o /1 = 360 o.
5sin(A+30 o) 5sinA को 30 o तक ले जाता है अर्थात। 30 o पहले शुरू होता है।
ग्राफ y=5sin(A+30 o) (साइनसॉइड)।

उदाहरण 6
प्लॉट y=7sin(2A-π/3) A=0 o से A=360 o की सीमा में।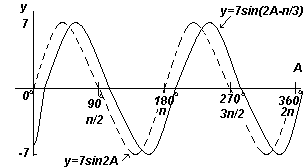

समाधान:
आयाम = 7, आवर्त = 2π/2= रेडियन
सामान्य रूप में y=sin(pt-α) y=sinpt से α/p . के सापेक्ष पिछड़ जाता है, इसलिए 7sin(2A-π/3) 7sin2A के सापेक्ष (π/3)/2 से पिछड़ जाता है, अर्थात। प्रति π/6 रेडियन या 30 o

असिन (ωt±α) के रूप का साइनसॉइड। अवस्था कोण। चरण में बदलाव।

चलो या अंजीर में। बाईं ओर एक सदिश है जो रेडियन/सेकेंड की गति से O के चारों ओर स्वतंत्र रूप से वामावर्त घूम रहा है। घूमने वाले वेक्टर को कहा जाता है चरण वेक्टर. t सेकंड के समय के बाद, OR कोण ωt रेडियन से घूमेगा (बाईं ओर की आकृति में, यह कोण TOR है)। यदि ST को OR के लंबवत बनाया गया है, तो sinωt=ST/OT, यानी। एसटी = ओटीसिनωt।
यदि ऐसे सभी ऊर्ध्वाधर घटकों को y बनाम t के एक भूखंड पर प्रक्षेपित किया जाता है, तो आयाम के साथ एक साइनसॉइड OR प्राप्त किया जाएगा।

यदि चरण सदिश OR T सेकंड में एक चक्कर (अर्थात 2π रेडियन) बनाता है, तो कोणीय वेग ω=2π/T rad/s, कहाँ से
Т=2π/ (ओं), जहां
टी is अवधि
1 सेकंड में गुजरने वाले पूर्ण आवर्त की संख्या कहलाती है आवृत्तिएफ।
आवृत्ति = (अवधि की संख्या)/(सेकंड) = 1/ टी = ω/2π हर्ट्ज,वे। च = ω/2π हर्ट्ज
इसलिए, कोणीय वेग
=2πf रेड/एस।

यदि सामान्य रूप से साइनसोइडल फ़ंक्शन y=sin(ωt± α) जैसा दिखता है, तो
ए - आयाम
- कोणीय वेग
2π/ - अवधि टी, एस
ω/2π - आवृत्ति च, हर्ट्ज
α रेडियन में लेड या लैग एंगल (y=Аsinωt के सापेक्ष) है, इसे फेज एंगल भी कहा जाता है।

उदाहरण 7
प्रत्यावर्ती धारा के रूप में दिया जाता है i=20sin(90πt+0.26) amps। आयाम, अवधि, आवृत्ति और चरण कोण (डिग्री में) निर्धारित करें

समाधान:
मैं \u003d 20sin (90πt + 0.26) ए, इसलिए,
आयाम है 20 ए
कोणीय वेग=90π, इसलिए,
अवधि टी= 2π/ = 2π/ 90π = 0.022 s = 22ms
आवृत्ति एफ\u003d 1 / टी \u003d 1 / 0.022 \u003d 45.46 हर्ट्ज
चरण कोण α= 0.26 रेड। \u003d (0.26 * 180 / ) ओ \u003d 14.9 ओ।

उदाहरण 8
ऑसिलेटिंग मैकेनिज्म का अधिकतम विस्थापन 3 मीटर और आवृत्ति 55 हर्ट्ज है। समय t=0 पर विस्थापन 100cm है। बदलाव को सामान्य रूप Аsin(ωt± α) में व्यक्त करें।

समाधान
आयाम = अधिकतम विस्थापन = 3m
कोणीय वेग ω=2πf = 2π(55) = 110 rad/s
इसलिए, विस्थापन 3sin(110πt + α) m है।
टी = 0 ऑफसेट = 100 सेमी = 1 मीटर पर।
इसलिए, 1= 3sin(0 + α), यानी। sinα=1/3=0.33
इसलिए α=arcsin0,33=19 o
तो ऑफसेट 3sin (110 t + 0.33) है।

उदाहरण 9
किसी भी t सेकंड में AC परिपथ में तात्कालिक वोल्टेज का मान v=350sin(40πt-0.542)V के रूप में दिया जाता है। पाना:
ए) आयाम, अवधि, आवृत्ति और चरण कोण (डिग्री में)
बी) टी = 0 . पर वोल्टेज मान
सी) टी = 10 एमएस . पर वोल्टेज मान
d) पहली बार वोल्टेज को 200 V तक पहुंचने में लगने वाला समय।
समाधान:
ए) आयाम 350 वी है, कोणीय वेग ω=40π . है
इसलिये,
अवधि Т=2π/ ω=2π/40π=0.05 s =50ms
आवृत्ति f=1/T=1/0.05=20 हर्ट्ज
चरण कोण \u003d 0.542 रेड (0.542 * 180 / π) \u003d 31 ओ v \u003d 350sin (40πt) के सापेक्ष देरी के साथ
बी) यदि टी \u003d 0, तो वी \u003d 350sin (0-0.542) \u003d 350sin (-31 ओ) \u003d -180.25 वी
ग) यदि t \u003d 10 ms, तो v \u003d 350sin (40π10 / 10 3 -0.542) \u003d 350sin (0.714) \u003d 350sin41 o \u003d 229.6 V
d) यदि v=200 और, तो 200=350sin(40πt-0.542) 200/350=sin(40πt-0.542)

अनुसूची। दोलन तंत्र
(उदाहरण, साइनसॉइड)।

v=350sin(40πt-0.542) इसलिए, (40πt-0.542)=arcsin200/350=35 o या 0.611 रेड।
40πt= 0.611+0.542=1.153।
इसलिए, यदि v=200V, तो समय t=1.153/40π=9.179 ms

ज्या और कोज्या की ज्यामितीय परिभाषा

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α रेडियन में व्यक्त कोण है।

साइनससमकोण त्रिभुज के कर्ण और टांग के बीच कोण α का एक त्रिकोणमितीय फलन है, जो विपरीत पैर की लंबाई के अनुपात के बराबर है |BC| कर्ण की लंबाई तक |AB|।

कोसाइन (cos α)एक समकोण त्रिभुज के कर्ण और टांग के बीच कोण α का एक त्रिकोणमितीय फलन है, जो आसन्न पैर की लंबाई के अनुपात के बराबर है |AC| कर्ण की लंबाई तक |AB|।

त्रिकोणमितीय परिभाषा

उपरोक्त सूत्रों का उपयोग करके, आप एक न्यून कोण की ज्या और कोज्या ज्ञात कर सकते हैं। लेकिन आपको यह सीखने की ज़रूरत है कि मनमाने आकार के कोण के साइन और कोसाइन की गणना कैसे करें। एक समकोण त्रिभुज ऐसा अवसर नहीं देता है (एक अधिक कोण, उदाहरण के लिए, इसमें नहीं हो सकता); इसलिए, इन सूत्रों को एक विशेष मामले के रूप में शामिल करते हुए, साइन और कोसाइन की अधिक सामान्य परिभाषा की आवश्यकता है।

त्रिकोणमितीय वृत्त बचाव के लिए आता है। कुछ कोण दिया जाए; यह त्रिकोणमितीय वृत्त पर उसी नाम के बिंदु से मेल खाता है।

चावल। 2. साइन और कोसाइन की त्रिकोणमितीय परिभाषा

एक कोण की कोज्या एक बिंदु का भुज है। कोण की ज्या एक बिंदु की कोटि होती है।

अंजीर पर। 2 कोण को तीव्र लिया जाता है, और यह समझना आसान है कि यह परिभाषा सामान्य ज्यामितीय परिभाषा से मेल खाती है। वास्तव में, हम एक समकोण त्रिभुज देखते हैं जिसमें एक इकाई कर्ण O और एक न्यून कोण होता है। इस त्रिभुज का आसन्न पैर cos है (चित्र 1 से तुलना करें) और साथ ही बिंदु का भुज; विपरीत पैर पाप है (जैसा कि चित्र 1 में है) और साथ ही बिंदु की कोटि।

लेकिन अब हम पहली तिमाही के लिए बाध्य नहीं हैं और इस परिभाषा को किसी भी कोण तक विस्तारित करने का अवसर प्राप्त करते हैं। अंजीर पर। 3 दिखाता है कि कोण की ज्या और कोज्या दूसरी, तीसरी और चौथी तिमाही में क्या हैं।

चावल। 3. ज्या और कोज्या द्वितीय, तृतीय और चतुर्थ तिमाही में

ज्या और कोज्या का तालिका मान

शून्य कोण \(\LARGE 0^(\circ ) \)

बिंदु 0 का भुज 1 है, बिंदु 0 की कोटि 0 है। इसलिये,

cos 0 = 1 पाप 0 = 0

चित्र 4. शून्य कोण

कोण \(\LARGE \frac(\pi)(6) = 30^(\circ ) \)

हम एक समकोण त्रिभुज देखते हैं जिसमें एक इकाई कर्ण और 30° का न्यून कोण होता है। जैसा कि आप जानते हैं, 30 ° कोण के विपरीत पैर आधा कर्ण 1 के बराबर है; दूसरे शब्दों में, लंबवत पैर 1/2 के बराबर है और इसलिए,

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

हम पाइथागोरस प्रमेय का उपयोग करके क्षैतिज पैर पाते हैं (या, जो समान है, हम मूल त्रिकोणमितीय पहचान के अनुसार कोसाइन पाते हैं):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 ऐसा क्यों होता है? एक समबाहु त्रिभुज को काटें जिसकी ऊँचाई 2 भुजा हो! यह कर्ण 2, न्यून कोण 30° और छोटे पैर 1 के साथ दो समकोण त्रिभुजों में टूट जाता है।

अंजीर 5. कोण π / 6

कोण \(\LARGE \frac(\pi)(4) = 45^(\circ ) \)

इस मामले में, समकोण त्रिभुज समद्विबाहु है; 45° के कोण की ज्या और कोज्या एक दूसरे के बराबर होती हैं। आइए उन्हें अभी के लिए x से निरूपित करें। हमारे पास है:

\[ x^(2) + x^(2) = 1 \]

जहां से \(x=\frac(\sqrt(2) )(2) \). इसलिये,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

अंजीर 5. कोण π / 4

साइन और कोसाइन के गुण

स्वीकृत पदनाम

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

दौरा

फलन y = sin x और y = cos x 2π आवर्त आवर्त हैं।

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

समानता

साइन फ़ंक्शन विषम है। कोसाइन फ़ंक्शन सम है।

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

परिभाषा और मूल्यों के डोमेन, एक्स्ट्रेमा, वृद्धि, कमी

साइन और कोसाइन के मुख्य गुण तालिका में प्रस्तुत किए गए हैं ( एन- पूर्णांक)।

	\(\छोटा< x < \)	\(\छोटा -\pi + 2\pi n \) \(\small< x < \) \(\small 2\pi n \)
अवरोही	\(\छोटा \dfrac(\pi)2 + 2\pi n \)\(\छोटा< x < \) \(\छोटा \dfrac(3\pi)2 + 2\pi n \)	\(\छोटा 2\pi n \) \(\छोटा< x < \) \(\pi + \small 2\pi n \)
अधिकतम, \(\छोटा x = \) \(\छोटा \dfrac(\pi)2 + 2\pi n \)	\(\छोटा x = 2\pi n \)
मिनिमा, \(\छोटा x = \) \(\छोटा -\dfrac(\pi)2 + 2\pi n \)	\(\छोटा x = \) \(\छोटा \pi + 2\pi n \)
शून्य, \(\छोटा x = \pi n \)	\(\छोटा x = \dfrac(\pi)2 + \pi n \)
y-अक्ष के साथ प्रतिच्छेदन बिंदु, x = 0	वाई = 0	वाई = 1

साइन और कोसाइन युक्त मूल सूत्र

वर्गों का योग

\(\sin^2 x + \cos^2 x = 1 \)

ज्या और कोज्या योग और अंतर सूत्र

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

ज्या और कोज्या के गुणनफल के सूत्र

\(\sin x \cos y = \) \(\dfrac12 (\बड़ा [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\बड़ा [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\बड़ा [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\बड़ा [) 1 + \cos 2x (\बड़ा]) \)

योग और अंतर सूत्र

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

कोज्या द्वारा ज्या का व्यंजक

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

ज्या द्वारा कोज्या का व्यंजक

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

स्पर्शरेखा के रूप में अभिव्यक्ति

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

पर \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x)) \).

पर \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x)) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x)) \).

साइन और कोसाइन, स्पर्शरेखा और कोटैंजेंट की तालिका

यह तालिका तर्क के कुछ मूल्यों के लिए साइन और कोसाइन के मूल्यों को दर्शाती है।
[ img शैली = "अधिकतम-चौड़ाई: 500 पीएक्स; अधिकतम-ऊंचाई: 1080 पीएक्स;" src="tablitsa.png" alt="(!LANG: ज्या और कोज्या की तालिका" title="ज्या और कोज्या की तालिका" ]!}

जटिल चरों के माध्यम से व्यंजक

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

यूलर सूत्र

\(e^(iz) = \cos z + i \sin z \)

अतिपरवलयिक कार्यों के संदर्भ में व्यंजक

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

संजात

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) । सूत्रों की व्युत्पत्ति > > >

nवें क्रम के व्युत्पन्न:
\(\बाएं(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\बाएं(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

अभिन्न

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
यह भी देखें खंड अनिश्चितकालीन समाकलों की तालिका >>>

श्रृंखला में विस्तार

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

सेकेंट, कोसेकेंट

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

उलटा कार्य

साइन और कोसाइन के व्युत्क्रम कार्य क्रमशः आर्क्साइन और आर्ककोसाइन हैं।

आर्कसिन, आर्क्सिन

\(y = \arcsin x \) \(\बाएं\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\बाएं\(- \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

आर्ककोसाइन, आर्ककोस

\(y = \arccos x\) \(\बाएं\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

सन्दर्भ:
में। ब्रोंस्टीन, के.ए. सेमेंडेव, हायर एजुकेशनल इंस्टीट्यूशंस के इंजीनियरों और छात्रों के लिए गणित की हैंडबुक, लैन, 2009।

आपके ब्राउजर में जावास्क्रिप्ट अक्षम है।
गणना करने के लिए ActiveX नियंत्रण सक्षम होना चाहिए!

बिंदु A पर केंद्रित।
α रेडियन में व्यक्त कोण है।

स्पर्शरेखा ( tgα) एक त्रिकोणमितीय फलन है जो समकोण त्रिभुज के कर्ण और टांग के बीच के कोण α पर निर्भर करता है, जो विपरीत पैर की लंबाई के अनुपात के बराबर होता है |BC| आसन्न पैर की लंबाई तक |AB| .

कोटैंजेंट ( सीटीजीα) एक त्रिकोणमितीय फलन है जो एक समकोण त्रिभुज के कर्ण और टांग के बीच के कोण α पर निर्भर करता है, जो आसन्न टांग की लंबाई के अनुपात के बराबर है |AB| विपरीत पैर की लंबाई तक |BC| .

स्पर्शरेखा

कहां एन- पूरा का पूरा।

पश्चिमी साहित्य में, स्पर्शरेखा को निम्नानुसार दर्शाया गया है:
.
;
;
.

स्पर्शरेखा फलन का आलेख, y = tg x

कोटैंजेंट

कहां एन- पूरा का पूरा।

पश्चिमी साहित्य में, कोटैंजेंट को निम्नानुसार दर्शाया गया है:
.
निम्नलिखित संकेतन भी अपनाया गया है:
;
;
.

सहस्पर्शी फलन का आलेख, y = ctg x

स्पर्शरेखा और कोटैंजेंट के गुण

दौरा

कार्य y= टीजी एक्सऔर y= सीटीजी एक्सअवधि के साथ आवधिक हैं।

समानता

स्पर्शरेखा और कोटैंजेंट के फलन विषम हैं।

परिभाषा और मूल्यों के डोमेन, आरोही, अवरोही

फलन स्पर्शरेखा और कोटैंजेंट अपनी परिभाषा के क्षेत्र में निरंतर होते हैं (निरंतरता का प्रमाण देखें)। टेंगेंट और कोटैंजेंट के मुख्य गुण तालिका में प्रस्तुत किए गए हैं ( एन- पूर्णांक)।

	वाई = टीजी एक्स	वाई = सीटीजी एक्स
दायरा और निरंतरता
मूल्यों की श्रृंखला	-∞ < y < +∞	-∞ < y < +∞
आरोही		-
अवरोही	-
चरम	-	-
शून्य, y= 0
y-अक्ष के साथ प्रतिच्छेदन बिंदु, x = 0	वाई = 0	-

सूत्रों

ज्या और कोज्या के संदर्भ में व्यंजक

; ;
; ;
;

योग और अंतर के स्पर्शरेखा और कोटंगेंट के लिए सूत्र

शेष सूत्र प्राप्त करना आसान है, उदाहरण के लिए

स्पर्शरेखा का उत्पाद

स्पर्शरेखाओं के योग और अंतर का सूत्र

यह तालिका तर्क के कुछ मूल्यों के लिए स्पर्शरेखा और स्पर्शरेखा के मान दिखाती है।

सम्मिश्र संख्याओं के पदों में व्यंजक

अतिपरवलयिक कार्यों के संदर्भ में व्यंजक

;
;

संजात

; .

.
फ़ंक्शन के चर x के संबंध में nवें क्रम का व्युत्पन्न:
.
स्पर्शरेखा के लिए सूत्रों की व्युत्पत्ति > > > ; स्पर्शज्या के लिए > > >

अभिन्न

श्रृंखला में विस्तार

x की घातों में स्पर्शरेखा का विस्तार प्राप्त करने के लिए, आपको कार्यों के लिए एक घात श्रृंखला में विस्तार के कई पद लेने होंगे पाप xतथा क्योंकि xऔर इन बहुपदों को एक दूसरे में विभाजित करें। इससे निम्नलिखित सूत्र प्राप्त होते हैं।

पर ।

पर ।
कहाँ पे बी नहीं- बर्नौली संख्या। वे या तो पुनरावृत्ति संबंध से निर्धारित होते हैं:
;
;
कहाँ पे ।
या लाप्लास सूत्र के अनुसार:

उलटा कार्य

स्पर्शरेखा और कोटैन्जेन्ट के प्रतिलोम फलन क्रमशः चापस्पर्शी और चाप-स्पर्शी रेखा हैं।

आर्कटिक, आर्कटिक

, कहाँ पे एन- पूरा का पूरा।

चाप स्पर्शरेखा, arcctg

, कहाँ पे एन- पूरा का पूरा।

सन्दर्भ:
में। ब्रोंस्टीन, के.ए. सेमेंडेव, हायर एजुकेशनल इंस्टीट्यूशंस के इंजीनियरों और छात्रों के लिए गणित की हैंडबुक, लैन, 2009।
जी. कॉर्न, शोधार्थियों और इंजीनियरों के लिए गणित की पुस्तिका, 2012।

एक बिंदु पर केंद्रित ए.
α रेडियन में व्यक्त कोण है।

परिभाषा
साइनसएक त्रिकोणमितीय फलन है जो समकोण त्रिभुज के कर्ण और टांग के बीच के कोण α पर निर्भर करता है, जो विपरीत पैर की लंबाई के अनुपात के बराबर होता है |BC| कर्ण की लंबाई तक |AC|.

कोसाइन (cos α)एक त्रिकोणमितीय फलन है जो एक समकोण त्रिभुज के कर्ण और टांग के बीच के कोण α पर निर्भर करता है, जो आसन्न टांग की लंबाई के अनुपात के बराबर है |AB| कर्ण की लंबाई तक |AC|.

स्वीकृत पदनाम

;
;
.

ज्या फलन का ग्राफ, y = sin x

कोज्या फलन का ग्राफ, y = cos x

साइन और कोसाइन के गुण

दौरा

कार्य y= पाप xऔर y= क्योंकि xअवधि के साथ आवधिक 2 पाई.

समानता

साइन फ़ंक्शन विषम है। कोसाइन फ़ंक्शन सम है।

परिभाषा और मूल्यों का क्षेत्र, एक्स्ट्रेमा, वृद्धि, कमी

ज्या और कोज्या फलन उनकी परिभाषा के क्षेत्र पर निरंतर होते हैं, अर्थात सभी x के लिए (निरंतरता का प्रमाण देखें)। उनके मुख्य गुण तालिका (n - पूर्णांक) में प्रस्तुत किए गए हैं।

	वाई = पाप x	वाई = क्योंकि x
दायरा और निरंतरता	- ∞ < x < + ∞	- ∞ < x < + ∞
मूल्यों की श्रृंखला	-1 वाई 1	-1 वाई 1
आरोही
अवरोही
अधिकतम, y= 1
मिनिमा, y=- 1
शून्य, y= 0
y-अक्ष के साथ प्रतिच्छेदन बिंदु, x = 0	वाई = 0	वाई = 1

मूल सूत्र

वर्ग ज्या और कोज्या का योग

योग और अंतर के लिए ज्या और कोज्या सूत्र

;
;

ज्या और कोज्या के गुणनफल के सूत्र

योग और अंतर सूत्र

कोज्या द्वारा ज्या का व्यंजक

;
;
;
.

ज्या द्वारा कोज्या का व्यंजक

;
;
;
.

स्पर्शरेखा के रूप में अभिव्यक्ति

; .

के लिए, हमारे पास है:
; .

पर :
; .

साइन और कोसाइन, स्पर्शरेखा और कोटैंजेंट की तालिका

यह तालिका तर्क के कुछ मूल्यों के लिए साइन और कोसाइन के मूल्यों को दर्शाती है।

जटिल चरों के माध्यम से व्यंजक

;

यूलर सूत्र

अतिपरवलयिक कार्यों के संदर्भ में व्यंजक

;
;

संजात

; . सूत्रों की व्युत्पत्ति > > >

nवें क्रम के व्युत्पन्न:
{ -∞ < x < +∞ }

सेकेंट, कोसेकेंट

उलटा कार्य

साइन और कोसाइन के व्युत्क्रम कार्य क्रमशः आर्क्साइन और आर्ककोसाइन हैं।