Свойства на синуса и неговата графика. Свойства на синус, косинус, тангенс и котангенс

В тази статия ще покажем как дефиниции на синус, косинус, тангенс и котангенс на ъгъл и число в тригонометрията. Тук ще говорим за нотация, ще дадем примери за записи, ще дадем графични илюстрации. В заключение правим паралел между дефинициите на синус, косинус, тангенс и котангенс в тригонометрията и геометрията.

Навигация в страницата.

Определение на синус, косинус, тангенс и котангенс

Нека проследим как се формира понятието синус, косинус, тангенс и котангенс в училищния курс по математика. В уроците по геометрия се дава дефиницията на синус, косинус, тангенс и котангенс на остър ъгъл в правоъгълен триъгълник. И по-късно се изучава тригонометрията, която се отнася до синуса, косинуса, тангенса и котангенса на ъгъла на въртене и числото. Ние даваме всички тези определения, даваме примери и даваме необходимите коментари.

Остър ъгъл в правоъгълен триъгълник

От курса на геометрията са известни дефинициите на синуса, косинуса, тангенса и котангенса на остър ъгъл в правоъгълен триъгълник. Те са дадени като съотношение на страните на правоъгълен триъгълник. Представяме техните формулировки.

Определение.

Синус на остър ъгъл в правоъгълен триъгълнике съотношението на противоположния катет към хипотенузата.

Определение.

Косинус на остър ъгъл в правоъгълен триъгълнике съотношението на съседния катет към хипотенузата.

Определение.

Тангенс на остър ъгъл в правоъгълен триъгълнике съотношението на противоположния крак към съседния крак.

Определение.

Котангенс на остър ъгъл в правоъгълен триъгълнике съотношението на съседния крак към противоположния крак.

Там също се въвежда обозначението на синус, косинус, тангенс и котангенс – съответно sin, cos, tg и ctg.

Например, ако ABC е правоъгълен триъгълник с прав ъгъл C, тогава синусът на острия ъгъл A е равен на отношението на противоположния катет BC към хипотенузата AB, тоест sin∠A=BC/AB.

Тези дефиниции ви позволяват да изчислите стойностите на синуса, косинуса, тангенса и котангенса на остър ъгъл от известни дължини на страните на правоъгълен триъгълник, както и от известните стойности на синуса, косинуса, допирателна, котангенс и дължината на една от страните, намерете дължините на другите страни. Например, ако знаехме, че в правоъгълен триъгълник катетът AC е 3, а хипотенузата AB е 7, тогава бихме могли да изчислим косинуса на острия ъгъл A по дефиниция: cos∠A=AC/AB=3/7.

Ъгъл на въртене

В тригонометрията те започват да гледат на ъгъла по-широко – въвеждат понятието ъгъл на въртене. Ъгълът на въртене, за разлика от острия ъгъл, не е ограничен до кадри от 0 до 90 градуса, ъгълът на въртене в градуси (и в радиани) може да бъде изразен с всяко реално число от −∞ до +∞.

В тази светлина дефинициите на синуса, косинуса, тангенса и котангенса вече не са остър ъгъл, а ъгъл с произволна величина - ъгълът на въртене. Те са дадени чрез координатите x и y на точка A 1 , в която преминава т. нар. начална точка A(1, 0), след като се завърти на ъгъл α около точка O - началото на правоъгълна декартова координатна система и центъра на единичната окръжност.

Определение.

Синус на ъгъла на въртенеα е ордината на точка A 1 , тоест sinα=y .

Определение.

косинус на ъгъла на въртенеα се нарича абсцисата на точка A 1 , тоест cosα=x .

Определение.

Тангенс на ъгъла на въртенеα е отношението на ординатата на точка A 1 към нейната абсцисса, тоест tgα=y/x .

Определение.

Котангенс на ъгъла на въртенеα е отношението на абсцисата на точка A 1 към нейната ордината, тоест ctgα=x/y .

Синусът и косинусът са дефинирани за всеки ъгъл α, тъй като винаги можем да определим абсцисата и ординатата на точката, която се получава чрез завъртане на началната точка за ъгъла α. И тангенсът и котангенсът не са определени за нито един ъгъл. Тангенсът не е дефиниран за такива ъгли α, при които началната точка отива в точка с нулева абциса (0, 1) или (0, −1) и това става при ъгли 90°+180° k , k∈Z (π /2+π k rad). Всъщност при такива ъгли на завъртане изразът tgα=y/x няма смисъл, тъй като съдържа деление на нула. Що се отнася до котангенса, той не е дефиниран за такива ъгли α, при които началната точка отива в точка с нулева ордината (1, 0) или (−1, 0) и това е случаят за ъгли 180° k , k ∈Z (π k rad).

И така, синусът и косинусът са дефинирани за всякакви ъгли на въртене, тангенсът е дефиниран за всички ъгли с изключение на 90°+180° k , k∈Z (π/2+π k rad), а котангенсът е за всички ъгли с изключение на 180 ° ·k , k∈Z (π·k rad).

Вече познатите ни нотации се появяват в дефинициите sin, cos, tg и ctg, те също се използват за означаване на синус, косинус, тангенс и котангенс на ъгъла на въртене (понякога можете да намерите нотацията tan и cot, съответстваща на тангенс и котангенс). Така синусът на ъгъла на въртене от 30 градуса може да бъде записан като sin30°, записите tg(−24°17′) и ctgα съответстват на тангенса на ъгъла на въртене −24 градуса 17 минути и котангенса на ъгъла на въртене α . Припомнете си, че когато се записва радианската мярка на ъгъл, обозначението "rad" често се пропуска. Например, косинусът на ъгъл на завъртане от три pi rads обикновено се означава cos3 π .

В заключение на този параграф си струва да се отбележи, че когато говорим за синуса, косинуса, тангенса и котангенса на ъгъла на въртене, фразата „ъгъл на въртене“ или думата „въртене“ често се пропуска. Тоест, вместо фразата "синус на ъгъла на въртене алфа", обикновено се използва фразата "синус на ъгъла на алфа" или дори по-кратко - "синус на алфа". Същото важи и за косинус, допирателна и котангенс.

Да кажем също, че дефинициите на синуса, косинуса, тангенса и котангенса на остър ъгъл в правоъгълен триъгълник са в съответствие с току-що дадените дефиниции за синуса, косинуса, тангенса и котангенса на ъгъл на въртене, вариращ от 0 до 90 градуси. Ще обосноваваме това.

Числа

Определение.

Синус, косинус, тангенс и котангенс на число t е число, равно на синуса, косинуса, тангенса и котангенса на ъгъла на въртене в t радиани, съответно.

Например, косинусът от 8 π е по дефиниция число, равно на косинуса на ъгъл от 8 π rad. И косинусът на ъгъла в 8 π rad е равен на единица, следователно, косинусът на числото 8 π е равен на 1.

Има и друг подход към дефиницията на синуса, косинуса, тангенса и котангенса на число. Състои се във факта, че на всяко реално число t се приписва точка от единичната окръжност, центрирана в началото на правоъгълната координатна система, а синусът, косинусът, тангенсът и котангенсът се определят чрез координатите на тази точка. Нека се спрем на това по-подробно.

Нека покажем как се установява съответствието между реални числа и точки от окръжността:

• на числото 0 се приписва начална точка A(1, 0) ;
• положително число t е свързано с точка от единичната окръжност, до която ще стигнем, ако се движим около окръжността от началната точка в посока обратно на часовниковата стрелка и преминем през път с дължина t;
• отрицателно число t е свързано с точка от единичната окръжност, до която ще стигнем, ако се движим около окръжността от началната точка по посока на часовниковата стрелка и преминем през път с дължина |t| .

Сега нека преминем към определенията на синус, косинус, тангенс и котангенс на числото t. Да приемем, че числото t съответства на точка от окръжността A 1 (x, y) (например числото &pi/2; съответства на точка A 1 (0, 1) ).

Определение.

Синус на число t е ордината на единичната окръжност, съответстваща на числото t, тоест sint=y.

Определение.

Косинус на число t се нарича абсцисата на точката от единичната окръжност, съответстваща на числото t, тоест цена=x.

Определение.

Тангенс на число t е отношението на ординатата към абсцисата на точката от единичната окръжност, съответстваща на числото t, тоест tgt=y/x. В друга еквивалентна формулировка тангенсът на числото t е отношението на синуса на това число към косинуса, тоест tgt=sint/cost .

Определение.

Котангенс на число t е отношението на абсцисата към ординатата на точката на единичната окръжност, съответстваща на числото t, тоест ctgt=x/y. Друга формулировка е следната: тангенсът на числото t е отношението на косинуса на числото t към синуса на числото t : ctgt=cost/sint .

Тук отбелязваме, че току-що дадените дефиниции са в съответствие с определението, дадено в началото на този подраздел. Всъщност точката на единичната окръжност, съответстваща на числото t, съвпада с точката, получена чрез завъртане на началната точка през ъгъл от t радиана.

Също така си струва да се изясни този момент. Да приемем, че имаме запис sin3. Как да разберем дали става дума за синусът на числото 3 или за синуса на ъгъла на въртене от 3 радиана? Това обикновено е ясно от контекста, иначе вероятно няма значение.

Тригонометрични функции на ъглови и числови аргументи

Съгласно дефинициите, дадени в предишния параграф, всеки ъгъл на завъртане α съответства на добре дефинирана стойност на sinα, както и на стойността на cosα. В допълнение, всички ъгли на въртене, различни от 90°+180° k, k∈Z (π/2+π k rad), съответстват на стойностите tgα и различни от 180° k, k∈Z (π k rad) са стойностите на ctgα. Следователно sinα, cosα, tgα и ctgα са функции на ъгъла α. С други думи, това са функции на ъгловия аргумент.

По подобен начин можем да говорим за функциите синус, косинус, тангенс и котангенс на числов аргумент. Всъщност всяко реално число t съответства на добре дефинирана стойност на sint , както и на цената . Освен това всички числа, различни от π/2+π·k, k∈Z, съответстват на стойностите tgt, а числата π·k, k∈Z съответстват на стойностите ctgt.

Функциите синус, косинус, тангенс и котангенс се наричат основни тригонометрични функции.

Обикновено от контекста става ясно, че имаме работа с тригонометрични функции на ъглов аргумент или числен аргумент. В противен случай можем да разглеждаме независимата променлива и като мярка на ъгъла (аргументът на ъгъла) и като числов аргумент.

Училището обаче изучава основно числови функции, тоест функции, чиито аргументи, както и съответните стойности на функциите, са числа. Следователно, ако говорим за функции, тогава е препоръчително да се разглеждат тригонометричните функции като функции на числови аргументи.

Връзка на дефиниции от геометрия и тригонометрия

Ако разгледаме ъгъла на въртене α от 0 до 90 градуса, тогава данните в контекста на тригонометрията на дефиницията на синуса, косинуса, тангенса и котангенса на ъгъла на въртене са напълно съвместими с дефинициите на синуса, косинуса , тангенс и котангенс на остър ъгъл в правоъгълен триъгълник, които са дадени в курса по геометрия. Нека обосноваваме това.

Начертайте единична окръжност в правоъгълната декартова координатна система Oxy. Обърнете внимание на началната точка A(1, 0) . Нека го завъртим на ъгъл α, вариращ от 0 до 90 градуса, получаваме точката A 1 (x, y) . Нека пуснем перпендикуляра A 1 H от точка A 1 до оста Ox.

Лесно е да се види, че в правоъгълен триъгълник ъгълът A 1 OH е равен на ъгъла на завъртане α, дължината на крака OH, съседен на този ъгъл, е равна на абсцисата на точка A 1, тоест |OH | |=x, дължината на катета A 1 H срещу ъгъла е равна на ординатата на точка A 1 , тоест |A 1 H|=y , а дължината на хипотенузата OA 1 е равна на единица , тъй като това е радиусът на единичната окръжност. Тогава, по дефиниция от геометрията, синусът на остър ъгъл α в правоъгълен триъгълник A 1 OH е равен на отношението на противоположния катет към хипотенузата, тоест sinα=|A 1 H|/|OA 1 |= y/1=y . И по дефиниция от тригонометрията, синусът на ъгъла на завъртане α е равен на ординатата на точка A 1, тоест sinα=y. Това показва, че определението на синуса на остър ъгъл в правоъгълен триъгълник е еквивалентно на дефиницията на синуса на ъгъла на въртене α за α от 0 до 90 градуса.

По подобен начин може да се покаже, че дефинициите на косинуса, тангенса и котангенса на остър ъгъл α са в съответствие с дефинициите на косинуса, тангенса и котангенса на ъгъла на въртене α.

Библиография.

1. Геометрия. 7-9 клас: проучвания. за общо образование институции / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. - 20-то изд. М.: Образование, 2010. - 384 с.: ил. - ISBN 978-5-09-023915-8.
2. Погорелов A.V.Геометрия: Proc. за 7-9 клетки. общо образование институции / А. В. Погорелов. - 2-ро изд. - М.: Просвещение, 2001. - 224 с.: ил. - ISBN 5-09-010803-X.
3. Алгебра и елементарни функции: Учебник за ученици от 9 клас на СОУ / Е. С. Кочетков, Е. С. Кочеткова; Под редакцията на доктора на физико-математическите науки О. Н. Головин - 4-то изд. Москва: Образование, 1969.
4. алгебра: Proc. за 9 клетки. средно училище / Ю. Н. Макаричев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Изд. С. А. Теляковски.- М.: Просвещение, 1990.- 272 с.: Ил.- ISBN 5-09-002727-7
5. алгебраи началото на анализа: Proc. за 10-11 клетки. общо образование институции / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др.; Изд. А. Н. Колмогорова.- 14-то изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
6. Мордкович А.Г.Алгебра и началото на анализа. 10 клас. В 14 ч. Част 1: учебник за образователни институции (профилно ниво) / A. G. Mordkovich, P. V. Semenov. - 4-то изд., доп. - М.: Мнемозина, 2007. - 424 с.: ил. ISBN 978-5-346-00792-0.
7. алгебраи началото на математическия анализ. 10 клас: учебник. за общо образование институции: основни и профилни. нива /[Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; изд. А. Б. Жижченко. - 3-то изд. - I .: Образование, 2010. - 368 с.: Ил. - ISBN 978-5-09-022771-1.
8. Башмаков М.И.Алгебра и началото на анализа: учеб. за 10-11 клетки. средно училище - 3-то изд. - М.: Просвещение, 1993. - 351 с.: ил. - ISBN 5-09-004617-4.
9. Гусев В. А., Мордкович А. Г.Математика (наръчник за кандидатстващи в техникумите): учеб. надбавка.- М.; По-висок училище, 1984.-351 с., ил.

От графиките може да се види, че:

1. Синусите и косинусите варират между -1 и 1
2. Косинусовата крива има същата форма като синусоидата, но е изместена спрямо нея с 90 o
3. Синус и косинус криви са непрекъснати и се повтарят с период от 360 o , допирателната крива има прекъсвания и се повтаря с период от 180 o .

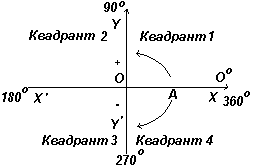На фиг. отляво са показани перпендикулярни оси XX" и YY"; пресичащи се в началото O. При работа с графики измерванията вдясно и нагоре от O се считат за положителни, наляво и надолу от O - за отрицателни. Нека OA се върти свободно спрямо O. Когато OA се върти обратно на часовниковата стрелка, измереният ъгъл се счита за положителен, а когато се върти по посока на часовниковата стрелка, той е отрицателен.

График. положителен или отрицателен
посока в кръгово движение.

Нека OA се върти обратно на часовниковата стрелка по такъв начин, че Θ 1 да е произволен ъгъл в първия квадрант, и построете перпендикуляр AB, за да получите правоъгълен триъгълник OAB на фиг. наляво. Тъй като и трите страни на триъгълника са положителни, тригонометричните функции синус, косинус и тангенс в първия квадрант ще бъдат положителни. (Обърнете внимание, че дължината на OA винаги е положителна, защото е радиусът на окръжността.)
Нека OA се върти по-нататък по такъв начин, че Θ 2 да е произволен ъгъл във втория квадрант, и конструирайте AC така, че да се образува правоъгълен триъгълник OAC. Тогава sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Нека OA се върти по-нататък по такъв начин, че Θ 3 да е произволен ъгъл в третия квадрант, и конструирайте AD така, че да се образува правоъгълен триъгълник OAD. Тогава sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

График. Изграждане на ъгли в
различни квадранти.

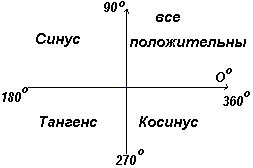Нека OA се върти по-нататък по такъв начин, че Θ 4 да е произволен ъгъл в четвъртия квадрант, и конструирайте AE така, че да се образува правоъгълен триъгълник OAE. Тогава sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

В първия квадрант всички тригонометрични функции имат положителни стойности, във втория само синусът е положителен, в третия само тангенсът, в четвъртия само косинусът, който е показан на фиг. наляво.

Познаването на ъглите с произволна величина е необходимо, когато се намират, например, всички ъгли между 0 o и 360 o, чийто синус е, да речем, 0,3261. Ако въведете 0,3261 в калкулатора и натиснете бутона sin -1, ще получите отговора 19,03 o. Има обаче втори ъгъл между 0 o и 360 o, който калкулаторът няма да покаже. Синусът също е положителен във втория квадрант. Другият ъгъл е показан на фиг. по-долу като ъгъл Θ, където Θ=180 o - 19,03 o = 160,97 o . Така 19,03 o и 160,97 o са ъгли в диапазона от 0 o до 360 o, чийто синус е 0,3261.

Бъди внимателен! Калкулаторът дава само една от тези стойности. Втората стойност трябва да се определи според теорията на ъглите с произволна величина.

Пример 1

Намерете всички ъгли между 0 o и 360 o, чийто синус е -0,7071

Решение:
Ъглите, чийто синус е -0,7071 o, са в третия и четвъртия квадранти, тъй като синусът е отрицателен в тези квадранти (виж фигурата вляво).

График. Намиране на всички ъгли по
дадена стойност на синусите (пример)

От следващата фигура Θ = arcsin 0,7071 = 45 o . Два ъгъла в диапазона от 0 o до 360 o, чийто синус е -0,7071, са 180 o +45 o \u003d 225 o и 360 o - 45 o \u003d 315 o.

Забележка.Калкулаторът дава само един отговор.
График. Намиране на всички ъгли по
дадена стойност на синусите (пример)

Пример 2

Намерете всички ъгли между 0 o и 360 o, чиято тангенс е 1,327.

Решение:
Допирателната е положителна в първи и трети квадрант - фиг. наляво.
График. Намиране на всички ъгли по

От фигурата по-долу Θ = arctan1,327= 53 o .
Два ъгъла в диапазона от 0 o до 360 o, чиито тангенс е 1,327, са 53 o и 180 o + 53 o , т.е. 233o.
График. Намиране на всички ъгли по
дадена допирателна стойност (пример)

Нека ИЛИ на фиг. отляво е вектор с единична дължина, свободно въртящ се обратно на часовниковата стрелка около O. Един оборот произвежда кръга, показан на фиг. и разделено на сектори от 15 o . Всеки радиус има хоризонтална и вертикална компонента. Например, за 30 o вертикалният компонент е TS, а хоризонталният компонент е OS.

От определението на тригонометричните функции
sin30 o =TS/TO=TS/1, т.е. TS=sin30oи cos30 o =OS/TO=OS/1, т.е. OS=cos30o

Вертикалният компонент TS може да бъде начертан като T"S", което е равно на стойността, съответстваща на ъгъла от 30° в графиката на ъгъла y спрямо x. Ако всички вертикални компоненти, като TS, се прехвърлят в графиката, тогава ще се получи синусоида, показана на фиг. по-горе.

Ако всички хоризонтални компоненти, като OS, се проектират върху графика на y срещу x, получавате косинусова вълна. Тези проекции са лесни за визуализиране чрез преначертаване на кръг с радиус ИЛИ и ъгли, произхождащи от вертикала, както е показано на фигурата вляво.
От фиг. отляво можете да видите, че синусоидата има същата форма като косинусовата вълна, но изместена с 90 o .

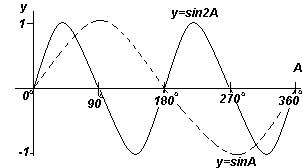Периодични функции и период
Всяка от графиките на функциите, показани на четирите фиг. по-горе, се повтаря с увеличаване на ъгъла А, така се наричат периодични функции.
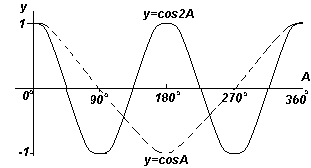
Функциите y=sinA и y=cosA се повтарят на всеки 360 o (или 2π радиана), така че 360 o се нарича Периодтези функции. Функциите y=sin2A и y=cos2A се повтарят на всеки 180 o (или π радиана), така че 180 o е периодът за тези функции.
Като цяло, ако y=sinpA и y=cospA (където p е константа), тогава периодът на функцията е 360 o /p (или 2π/p радиана). Следователно, ако y=sin3A, тогава периодът на тази функция е 360 o /3= 120 o , ако y=cos4A, тогава периодът на тази функция е 360 o /4= 90 o .

Амплитуда
Амплитуданаречена максимална стойност на синусоидата. Всяка от графиките 1-4 има амплитуда от +1 (т.е. те се колебаят между +1 и -1). Въпреки това, ако y=4sinA, всяка от стойностите на sinA се умножава по 4, така че максималната стойност на амплитудата е 4. По същия начин, за y=5cos2A, амплитудата е 5 и периодът е 360 o /2= 180 o .

Пример 3
Изградете y=3sin2A в диапазона от A= 0 o до A=360 o .

Решение:
Амплитуда =3, период = 360 o /2 =180 o .

Пример 4
Графика y=4cos2x в диапазона от x=0 o до x=360 o

Решение:
Амплитуда = 4. период = 360 o /2 =180 o .

Закъснение и предни ъгли
Синус и косинус криви не винаги започват от 0o. За да се вземе предвид това обстоятелство, периодичната функция се представя като y=sin(A± α), където α е фазовото изместване по отношение на y=sinA и y=cosA.

След като съставите таблица със стойности, можете да начертаете функцията y=sin(A-60 o), показана на фиг. наляво. Ако кривата y=sinA започва от 0 o , тогава кривата y=sin(A-60 o ) започва от 60 o (т.е. нейната нулева стойност е 60 o вдясно). Така се казва, че y=sin(A-60o) късенспрямо y=sinA с 60°.
График. y=sin(A-60 o) (синусоидална вълна).

След като съставите таблица със стойности, можете да начертаете функцията y=cos(A+45 o), показана на фиг. По-долу.
Ако кривата y=cosA започва от 0 o , тогава кривата y=cos(A+45 o) започва на 45 o вляво (т.е. нейната нулева стойност е 45 o по-рано).
По този начин се казва, че графикът е y=cos(A+45 o) изпреварваграфика y=cosA при 45°.
График. y=cos(A+45 o) (косинус).

Като цяло графиката y=sin(A-α) изостава спрямо y=sinA с ъгъл α.
Косинусовата вълна има същата форма като синусоидата, но започва на 90 o вляво, т.е. пред нея с 90 o . Следователно, cosA=sin(A+90o).

Пример 5
Графика y=5sin(A+30 o) в диапазона от A=0 o до A=360 o

Решение:
Амплитуда = 5, период = 360 o /1 = 360 o .
5sin(A+30 o) води 5sinA с 30 o, т.е. започва 30 часа по-рано.
Графика y=5sin(A+30o) (синусоида).

Пример 6
Графика y=7sin(2A-π/3) в диапазона от A=0 o до A=360 o .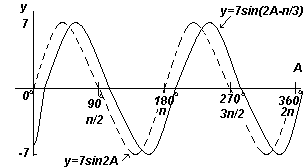

Решение:
Амплитуда = 7, период = 2π/2= π радиана
Общо взето y=sin(pt-α) изостава спрямо y=sinpt с α/p, следователно 7sin(2A-π/3) изостава спрямо 7sin2A с (π/3)/2, т.е. на π/6 радиана или 30 o

Синусоида от формата Asin(ωt±α). фазов ъгъл. Фазово изместване.

Нека ИЛИ на фиг. отляво е вектор, свободно въртящ се обратно на часовниковата стрелка около O със скорост ω радиана/сек. Въртящият се вектор се нарича фазов вектор. След време от t секунди ИЛИ ще се завърти през ъгъла ωt радиани (на фигурата вляво това е ъгълът TOR). Ако ST е конструиран перпендикулярно на OR, тогава sinωt=ST/OT, т.е. ST=OTsinωt.
Ако всички такива вертикални компоненти се проектират върху графика на y спрямо ωt, ще се получи синусоида с амплитуда OR.

Ако фазовият вектор ИЛИ направи един оборот (т.е. 2π радиана) за T секунди, тогава ъгловата скорост ω=2π/T rad/s, откъдето
Т=2π/ ω (s), където
Т е Период
Извиква се броят на пълните периоди, които преминават за 1 секунда честотае.
Честота = (брой периоди)/(секунда) = 1/ T = ω/2π Hz,тези. f= ω/2π Hz
Следователно ъгловата скорост
ω=2πf rad/s.

Ако като цяло синусоидалната функция изглежда като y=sin(ωt± α), тогава
А - амплитуда
ω - ъглова скорост
2π/ ω - период T, s
ω/2π - честота f, Hz
α е ъгълът на изпреварване или изоставане (спрямо y=Аsinωt) в радиани, нарича се още фазов ъгъл.

Пример 7
Променливият ток е даден като i=20sin(90πt+0,26) ампера. Определете амплитуда, период, честота и фазов ъгъл (в градуси)

Решение:
i \u003d 20sin (90πt + 0,26) A, следователно,
амплитудата е 20 А
ъглова скорост ω=90π, следователно,
период Т= 2π/ ω = 2π/ 90π = 0,022 s = 22 мс
честота е\u003d 1 / T = 1 / 0,022 \u003d 45,46 Hz
фазов ъгъл α= 0,26 рад. \u003d (0,26 * 180 / π) o \u003d 14,9 o.

Пример 8
Осцилиращият механизъм има максимално изместване 3 m и честота 55 Hz. В момент t=0 изместването е 100 cm. Изразете изместването в общата форма Аsin(ωt± α).

Решение
Амплитуда = максимална денивелация = 3m
Ъглова скорост ω=2πf = 2π(55) = 110 rad/s
Следователно изместването е 3sin(110πt + α) m.
При t=0 отместване = 100cm=1m.
Следователно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следователно α=arcsin0,33=19 o
Така че отместването е 3sin(110 πt + 0,33).

Пример 9
Стойността на моментното напрежение във веригата за променлив ток във всеки t секунди се дава като v=350sin(40πt-0.542)V. Намирам:
а) Амплитуда, период, честота и фазов ъгъл (в градуси)
б) стойност на напрежението при t = 0
в) стойност на напрежението при t = 10 ms
г) времето, необходимо на напрежението да достигне 200 V за първи път.
Решение:
а) Амплитудата е 350 V, ъгловата скорост е ω=40π
следователно,
период Т=2π/ ω=2π/40π=0.05 s =50ms
честота f=1/T=1/0.05=20 Hz
фазов ъгъл \u003d 0,542 rad (0,542 * 180 / π) = 31 o със закъснение спрямо v = 350sin (40πt)
b) Ако t = 0, тогава v = 350sin (0-0,542) = 350sin (-31 o) = -180,25 V
в) Ако t = 10 ms, тогава v = 350sin (40π10 / 10 3 -0,542) = 350sin (0,714) = 350sin41 o = 229,6 V
г) Ако v=200 И, тогава 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

График. Осцилиращ механизъм
(пример, синусоида).

v=350sin(40πt-0.542) Следователно, (40πt-0.542)=arcsin200/350=35 o или 0.611 rad.
40πt= 0,611+0,542=1,153.
Следователно, ако v=200V, тогава времето t=1,153/40π=9,179 ms

Геометрична дефиниция на синус и косинус

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α е ъгъл, изразен в радиани.

Синусе тригонометрична функция на ъгъла α между хипотенузата и катета на правоъгълен триъгълник, равна на съотношението на дължината на противоположния катет |BC| на дължината на хипотенузата |AB|.

косинус (cos α)е тригонометрична функция на ъгъла α между хипотенузата и катета на правоъгълен триъгълник, равна на съотношението на дължината на съседния катет |AC| на дължината на хипотенузата |AB|.

Тригонометрично определение

Използвайки горните формули, можете да намерите синуса и косинуса на остър ъгъл. Но трябва да научите как да изчислите синуса и косинуса на ъгъл с произволен размер. Правоъгълният триъгълник не дава такава възможност (тъп ъгъл, например, не може да бъде в него); следователно е необходимо по-общо определение на синус и косинус, съдържащо тези формули като специален случай.

На помощ идва тригонометричният кръг. Нека е даден някакъв ъгъл; отговаря на едноименната точка на тригонометричния кръг.

Ориз. 2. Тригонометрично определение на синус и косинус

Косинусът на ъгъла е абсцисата на точка. Синусът на ъгъла е ордината на точка.

На фиг. 2 ъгълът се приема остър и е лесно да се разбере, че това определение съвпада с общото геометрично определение. Наистина виждаме правоъгълен триъгълник с единична хипотенуза O и остър ъгъл. Съседният катет на този триъгълник е cos (сравнете с фиг. 1) и в същото време абсцисата на точката; противоположният крак е sin (както на фиг. 1) и в същото време ордината на точката.

Но сега вече не сме ограничени от първото тримесечие и получаваме възможността да разширим това определение до всякакъв ъгъл. На фиг. 3 показва какви са синусът и косинусът на ъгъла във втората, третата и четвъртата четвърт.

Ориз. 3. Синус и косинус във II, III и IV четвърти

Таблица със стойности на синус и косинус

Нулев ъгъл \(\ LARGE 0^(\circ ) \)

Абсцисата на точка 0 е 1, ординатата на точка 0 е 0. следователно,

cos 0 = 1 sin 0 = 0

Фиг. 4. Нулев ъгъл

Ъгъл \(\ LARGE \ frac(\pi)(6) = 30^(\circ ) \)

Виждаме правоъгълен триъгълник с единична хипотенуза и остър ъгъл 30°. Както знаете, кракът срещу ъгъла 30 ° е равен на половината от хипотенузата 1; с други думи, вертикалният крак е равен на 1/2 и следователно,

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Намираме хоризонталния крак с помощта на питагоровата теорема (или, което е същото, намираме косинуса според основната тригонометрична идентичност):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 Защо се случва това? Изрежете равностранен триъгълник със страна 2 по височината му! Разпада се на два правоъгълни триъгълника с хипотенуза 2, остър ъгъл 30° и по-малък катет 1.

Фиг.5. Ъгъл π / 6

Ъгъл \(\ LARGE \frac(\pi)(4) = 45^(\circ ) \)

В този случай правоъгълният триъгълник е равнобедрен; синусът и косинусът на ъгъл от 45° са равни един на друг. Нека ги обозначим за сега с x. Ние имаме:

\[ x^(2) + x^(2) = 1 \]

откъдето \(x=\frac(\sqrt(2) )(2) \). следователно,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Фиг.5. Ъгъл π / 4

Свойства на синус и косинус

Приети обозначения

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Периодичност

Функциите y = sin x и y = cos x са периодични с период 2π.

\(\sin(x + 2\pi) = \sin x; \quad\)\(\cos(x + 2\pi) = \cos x \)

Паритет

Функцията синус е нечетна. Косинусовата функция е четна.

\(\sin(-x) = - \sin x; \quad\)\(\cos(-x) = \cos x \)

Домени на дефиниция и стойности, екстремуми, увеличение, намаление

Основните свойства на синуса и косинуса са представени в таблицата ( н- цяло число).

	\(\малък< x < \)	\(\small -\pi + 2\pi n \) \(\small< x < \) \(\small 2\pi n \)
Низходящо	\(\small \dfrac(\pi)2 + 2\pi n \)\(\малък< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \)	\(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \)
Максимум, \(\small x = \) \(\small \dfrac(\pi)2 + 2\pi n \)	\(\small x = 2\pi n \)
Минимум, \(\small x = \) \(\small -\dfrac(\pi)2 + 2\pi n \)	\(\small x = \) \(\small \pi + 2\pi n \)
Нули, \(\small x = \pi n \)	\(\small x = \dfrac(\pi)2 + \pi n \)
Точки на пресичане с оста y, x = 0	y=0	y=1

Основни формули, съдържащи синус и косинус

Сума от квадрати

\(\sin^2 x + \cos^2 x = 1 \)

Формули за синус и косинус на сума и разлика

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \вдясно) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Формули за произведението на синуси и косинуси

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)

Формули за сума и разлика

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Изразяване на синус чрез косинус

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Изразяване на косинус чрез синус

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Изразяване чрез допирателна

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

В \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

В \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Таблица на синуси и косинуси, тангенси и котангенси

Тази таблица показва стойностите на синусите и косинусите за някои стойности на аргумента.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="(!LANG: Таблица на синусите и косинусите" title="Таблица на синусите и косинусите" ]!}

Изрази чрез комплексни променливи

\(i^2 = -1 \)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

формула на Ойлер

\(e^(iz) = \cos z + i \sin z \)

Изрази в термини на хиперболични функции

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Производни

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Извеждане на формули >>>

Производни от n-ти порядък:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

Интеграли

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Вижте също раздел Таблица на неопределените интеграли >>>

Разширения в серии

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \инфти< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Секанс, косеканс

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x) \)

Обратни функции

Обратните функции на синус и косинус са съответно арксинус и арккосинус.

Арксин, арксин

\(y = \arcsin x \) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

Аркосинус, арккос

\(y = \arccos x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Препратки:
И.Н. Бронщайн, К.А. Семендяев, Наръчник по математика за инженери и студенти от висши учебни заведения, Лан, 2009.

Javascript е деактивиран във вашия браузър.
ActiveX контролите трябва да бъдат активирани, за да се правят изчисления!

Центрирано в точка А.
α е ъгълът, изразен в радиани.

допирателна ( tgα) е тригонометрична функция, зависеща от ъгъла α между хипотенузата и катета на правоъгълен триъгълник, равна на съотношението на дължината на противоположния катет |BC| до дължината на съседния крак |AB| .

котангенс ( ctgα) е тригонометрична функция, зависеща от ъгъла α между хипотенузата и катета на правоъгълен триъгълник, равна на съотношението на дължината на съседния катет |AB| до дължината на противоположния крак |BC| .

Тангента

Където н- цяла.

В западната литература допирателната се обозначава по следния начин:
.
;
;
.

Графика на допирателната функция, y = tg x

Котангенс

Където н- цяла.

В западната литература котангенсът се обозначава, както следва:
.
Също така е приета следната нотация:
;
;
.

Графика на котангенсната функция, y = ctg x

Свойства на тангенса и котангенса

Периодичност

Функции y= tg xи y= ctg xса периодични с период π.

Паритет

Функциите тангенс и котангенс са нечетни.

Области на дефиниция и стойности, възходящо, низходящо

Функциите допирателна и котангенс са непрекъснати в своята област на дефиниция (вижте доказателството за непрекъснатост). Основните свойства на тангенса и котангенса са представени в таблицата ( н- цяло число).

	y= tg x	y= ctg x
Обхват и приемственост
Диапазон от стойности	-∞ < y < +∞	-∞ < y < +∞
Възходящ		-
Низходящо	-
Крайности	-	-
Нули, y= 0
Точки на пресичане с оста y, x = 0	y= 0	-

Формули

Изрази по отношение на синус и косинус

; ;
; ;
;

Формули за тангенс и котангенс на сума и разлика

Останалите формули са лесни за получаване, например

Произведение на допирателните

Формулата за сбора и разликата на допирателните

Тази таблица показва стойностите на тангентите и котангентите за някои стойности на аргумента.

Изрази по отношение на комплексни числа

Изрази в термини на хиперболични функции

;
;

Производни

; .

.
Производна от n-ти ред по отношение на променливата x на функцията:
.
Извеждане на формули за допирателна > > > ; за котангенс > > >

Интеграли

Разширения в серии

За да получите разширението на допирателната по степени на x, трябва да вземете няколко члена на разширението в степенен ред за функциите грях хи cos xи разделете тези полиноми един на друг , . Това води до следните формули.

В .

в .
където B n- Числата на Бернули. Те се определят или от отношението на повторяемост:
;
;
където .
Или по формулата на Лаплас:

Обратни функции

Обратните функции на допирателната и котангенса са съответно арктангенс и арккотангенс.

Арктангенс, arctg

, където н- цяла.

Arc тангенс, arcctg

, където н- цяла.

Препратки:
И.Н. Бронщайн, К.А. Семендяев, Наръчник по математика за инженери и студенти от висши учебни заведения, Лан, 2009.
Г. Корн, Наръчник по математика за изследователи и инженери, 2012 г.

Центрирано в точка А.
α е ъгъл, изразен в радиани.

Определение
Синусе тригонометрична функция, зависеща от ъгъла α между хипотенузата и катета на правоъгълен триъгълник, равна на съотношението на дължината на противоположния катет |BC| на дължината на хипотенузата |AC|.

косинус (cos α)е тригонометрична функция, зависеща от ъгъла α между хипотенузата и катета на правоъгълен триъгълник, равна на съотношението на дължината на съседния катет |AB| на дължината на хипотенузата |AC|.

Приети обозначения

;
;
.

;
;
.

Графика на функцията синус, y = sin x

Графика на косинус функцията, y = cos x

Свойства на синус и косинус

Периодичност

Функции y= грях хи y= cos xпериодичен с точка 2 пи.

Паритет

Функцията синус е нечетна. Косинусовата функция е четна.

Област на дефиниция и стойности, екстремуми, увеличение, намаление

Функциите синус и косинус са непрекъснати в своята област на дефиниция, тоест за всички x (вижте доказателството за непрекъснатост). Основните им свойства са представени в таблицата (n - цяло число).

	y= грях х	y= cos x
Обхват и приемственост	- ∞ < x < + ∞	- ∞ < x < + ∞
Диапазон от стойности	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Възходящ
Низходящо
Максимум, y= 1
Минимум, y = - 1
Нули, y= 0
Точки на пресичане с оста y, x = 0	y= 0	y= 1

Основни формули

Сбор на квадрат синус и косинус

Формули за синус и косинус за сума и разлика

;
;

Формули за произведението на синуси и косинуси

Формули за сума и разлика

Изразяване на синус чрез косинус

;
;
;
.

Изразяване на косинус чрез синус

;
;
;
.

Изразяване чрез допирателна

; .

За, имаме:
; .

в :
; .

Таблица на синуси и косинуси, тангенси и котангенси

Тази таблица показва стойностите на синусите и косинусите за някои стойности на аргумента.

Изрази чрез комплексни променливи

;

формула на Ойлер

Изрази в термини на хиперболични функции

;
;

Производни

; . Извеждане на формули >>>

Производни от n-ти порядък:
{ -∞ < x < +∞ }

Секанс, косеканс

Обратни функции

Обратните функции на синус и косинус са съответно арксинус и арккосинус.

Арксин, арксин

Аркосинус, арккос

Препратки:
И.Н. Бронщайн, К.А. Семендяев, Наръчник по математика за инженери и студенти от висши учебни заведения, Лан, 2009.