คุณสมบัติของไซน์และกราฟ คุณสมบัติของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์

05.02.2022

ในบทความนี้ เราจะแสดงวิธีให้ คำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมและจำนวนในวิชาตรีโกณมิติ- ที่นี่เราจะพูดถึงสัญลักษณ์ ยกตัวอย่างรายการ และให้ภาพประกอบแบบกราฟิก โดยสรุป ให้เราวาดเส้นขนานระหว่างคำจำกัดความของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ในตรีโกณมิติและเรขาคณิต

การนำทางหน้า

คำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์

เรามาดูกันว่าแนวคิดของไซน์โคไซน์แทนเจนต์และโคแทนเจนต์เกิดขึ้นในหลักสูตรคณิตศาสตร์ของโรงเรียนอย่างไร ในบทเรียนเรขาคณิต จะให้คำจำกัดความของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของมุมแหลมในรูปสามเหลี่ยมมุมฉาก และต่อมามีการศึกษาตรีโกณมิติซึ่งพูดถึงไซน์, โคไซน์, แทนเจนต์และโคแทนเจนต์ของมุมการหมุนและจำนวน ให้เรานำเสนอคำจำกัดความทั้งหมดนี้ ยกตัวอย่าง และแสดงความคิดเห็นที่จำเป็น

มุมแหลมในรูปสามเหลี่ยมมุมฉาก

จากหลักสูตรเรขาคณิต เรารู้คำจำกัดความของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของมุมแหลมในรูปสามเหลี่ยมมุมฉาก พวกมันถูกกำหนดให้เป็นอัตราส่วนของด้าน สามเหลี่ยมมุมฉาก- ให้เราให้สูตรของพวกเขา

คำนิยาม.

ไซน์ของมุมแหลมในรูปสามเหลี่ยมมุมฉากคืออัตราส่วนของด้านตรงข้ามกับด้านตรงข้ามมุมฉาก

คำนิยาม.

โคไซน์ของมุมแหลมในรูปสามเหลี่ยมมุมฉากคืออัตราส่วนของขาที่อยู่ติดกันต่อด้านตรงข้ามมุมฉาก

คำนิยาม.

แทนเจนต์ของมุมแหลมในรูปสามเหลี่ยมมุมฉาก– นี่คืออัตราส่วนของด้านตรงข้ามกับด้านประชิด

คำนิยาม.

โคแทนเจนต์ของมุมแหลมในรูปสามเหลี่ยมมุมฉาก- นี่คืออัตราส่วนของด้านประชิดต่อด้านตรงข้าม

นอกจากนี้ยังมีการแนะนำการกำหนดไซน์, โคไซน์, แทนเจนต์และโคแทนเจนต์ด้วย - sin, cos, tg และ ctg ตามลำดับ

ตัวอย่างเช่น หาก ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุมฉาก C ดังนั้นไซน์ของมุมแหลม A จะเท่ากับอัตราส่วนของด้านตรงข้าม BC ต่อด้านตรงข้ามมุมฉาก AB นั่นคือ sin∠A=BC/AB

คำจำกัดความเหล่านี้ช่วยให้คุณสามารถคำนวณค่าของไซน์, โคไซน์, แทนเจนต์และโคแทนเจนต์ของมุมแหลมจากความยาวที่ทราบของด้านข้างของสามเหลี่ยมมุมฉากรวมถึงจากค่าที่ทราบของไซน์, โคไซน์, แทนเจนต์ โคแทนเจนต์และความยาวของด้านใดด้านหนึ่งเพื่อหาความยาวของด้านอื่นๆ ตัวอย่างเช่น หากเรารู้ว่าในสามเหลี่ยมมุมฉาก AC ขาเท่ากับ 3 และด้านตรงข้ามมุมฉาก AB เท่ากับ 7 เราก็สามารถคำนวณค่าโคไซน์ของมุมแหลม A ตามคำจำกัดความ: cos∠A=AC/ เอบี=3/7.

มุมการหมุน

ในวิชาตรีโกณมิติ พวกเขาเริ่มมองมุมให้กว้างขึ้น - พวกเขาแนะนำแนวคิดเรื่องมุมการหมุน ขนาดของมุมการหมุน ไม่เหมือนมุมแหลม ไม่จำกัดอยู่ที่ 0 ถึง 90 องศา มุมการหมุนในหน่วยองศา (และหน่วยเรเดียน) สามารถแสดงด้วยจำนวนจริงใดๆ ตั้งแต่ −∞ ถึง +∞

ในแง่นี้ คำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ไม่ได้กำหนดเป็นมุมแหลม แต่เป็นมุมที่มีขนาดตามอำเภอใจ - มุมการหมุน พวกมันจะได้รับผ่านพิกัด x และ y ของจุด A 1 ซึ่งจุดเริ่มต้นที่เรียกว่า A(1, 0) ไปตามการหมุนของมันด้วยมุม α รอบจุด O - จุดเริ่มต้นของระบบพิกัดคาร์ทีเซียนสี่เหลี่ยม และศูนย์กลางของวงกลมหน่วย

คำนิยาม.

ไซน์ของมุมการหมุนα คือลำดับของจุด A 1 นั่นคือ sinα=y

คำนิยาม.

โคไซน์ของมุมการหมุนα เรียกว่า abscissa ของจุด A 1 นั่นคือ cosα=x

คำนิยาม.

แทนเจนต์ของมุมการหมุนα คืออัตราส่วนของพิกัดของจุด A 1 ต่อจุดหักล้างของมัน นั่นคือ tanα=y/x

คำนิยาม.

โคแทนเจนต์ของมุมการหมุนα คืออัตราส่วนของ abscissa ของจุด A 1 ต่อพิกัด ซึ่งก็คือ ctgα=x/y

ไซน์และโคไซน์ถูกกำหนดไว้สำหรับมุม α ใดๆ เนื่องจากเราสามารถหาค่าแอบซิสซาและพิกัดของจุดได้เสมอ ซึ่งได้มาจากการหมุนจุดเริ่มต้นด้วยมุม α แต่แทนเจนต์และโคแทนเจนต์ไม่ได้ถูกกำหนดไว้สำหรับมุมใดๆ แทนเจนต์ไม่ได้ถูกกำหนดไว้สำหรับมุม α ซึ่งจุดเริ่มต้นไปยังจุดที่มีจุดหักมุมเป็นศูนย์ (0, 1) หรือ (0, −1) และสิ่งนี้เกิดขึ้นที่มุม 90°+180° k, k∈Z (π /2+π·k ราด) อันที่จริง ที่มุมการหมุนเช่นนั้น นิพจน์ tgα=y/x ไม่สมเหตุสมผล เนื่องจากนิพจน์มีการหารด้วยศูนย์ สำหรับโคแทนเจนต์นั้น ไม่ได้ถูกกำหนดไว้สำหรับมุม α ซึ่งจุดเริ่มต้นไปยังจุดที่มีพิกัดเป็นศูนย์ (1, 0) หรือ (−1, 0) และสิ่งนี้เกิดขึ้นสำหรับมุม 180° k, k ∈Z (π·เค ราด).

ดังนั้น ไซน์และโคไซน์ถูกกำหนดไว้สำหรับมุมการหมุนใดๆ แทนเจนต์ถูกกำหนดสำหรับทุกมุมยกเว้น 90°+180°k, k∈Z (π/2+πk rad) และโคแทนเจนต์ถูกกำหนดสำหรับทุกมุมยกเว้น 180° ·k , k∈Z (π·k ราด)

คำจำกัดความรวมถึงการกำหนดที่เราทราบอยู่แล้วว่า sin, cos, tg และ ctg และยังใช้เพื่อกำหนดไซน์, โคไซน์, แทนเจนต์และโคแทนเจนต์ของมุมการหมุน (บางครั้งคุณสามารถค้นหาการกำหนด tan และ cotที่สอดคล้องกับแทนเจนต์และโคแทนเจนต์) . ดังนั้นไซน์ของมุมการหมุน 30 องศาสามารถเขียนได้เป็น sin30° รายการ tg(−24°17′) และ ctgα สอดคล้องกับแทนเจนต์ของมุมการหมุน −24 องศา 17 นาที และโคแทนเจนต์ของมุมการหมุน α . โปรดจำไว้ว่าเมื่อเขียนหน่วยวัดเรเดียนของมุม มักจะละเว้นการกำหนด "rad" ตัวอย่างเช่น โคไซน์ของมุมการหมุนของสามไพราด มักจะเขียนแทน cos3·π

โดยสรุปประเด็นนี้ เป็นที่น่าสังเกตว่าเมื่อพูดถึงไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของมุมการหมุน วลี "มุมการหมุน" หรือคำว่า "การหมุน" มักถูกมองข้ามไป นั่นคือแทนที่จะใช้วลี "ไซน์ของมุมอัลฟาการหมุน" มักใช้วลี "ไซน์ของมุมอัลฟา" หรือที่สั้นกว่านั้นคือ "ไซน์อัลฟา" เช่นเดียวกับโคไซน์ แทนเจนต์ และโคแทนเจนต์

นอกจากนี้เรายังจะกล่าวอีกว่าคำจำกัดความของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของมุมแหลมในรูปสามเหลี่ยมมุมฉากนั้นสอดคล้องกับคำจำกัดความที่ให้ไว้สำหรับไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมการหมุนตั้งแต่ 0 ถึง 90 องศา เราจะพิสูจน์เรื่องนี้

ตัวเลข

คำนิยาม.

ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของจำนวน t คือตัวเลขที่เท่ากับไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมการหมุนในหน่วย t เรเดียน ตามลำดับ

ตัวอย่างเช่น โคไซน์ของตัวเลข 8·π ตามคำจำกัดความคือตัวเลขที่เท่ากับโคไซน์ของมุม 8·π rad และโคไซน์ของมุม 8·π rad เท่ากับ 1 ดังนั้น โคไซน์ของตัวเลข 8·π เท่ากับ 1

มีอีกวิธีหนึ่งในการกำหนดไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของตัวเลข ประกอบด้วยข้อเท็จจริงที่ว่าจำนวนจริง t แต่ละตัวสัมพันธ์กับจุดบนวงกลมหน่วยโดยมีจุดศูนย์กลางที่จุดกำเนิดของระบบพิกัดสี่เหลี่ยม และไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ถูกกำหนดผ่านพิกัดของจุดนี้ ลองดูรายละเอียดเพิ่มเติมนี้

ให้เราแสดงวิธีการโต้ตอบระหว่างจำนวนจริงและจุดบนวงกลม:

หมายเลข 0 ถูกกำหนดให้เป็นจุดเริ่มต้น A(1, 0);
จำนวนบวก t สัมพันธ์กับจุดบนวงกลมหน่วยซึ่งเราจะไปถึงถ้าเราเคลื่อนที่ไปตามวงกลมจากจุดเริ่มต้นในทิศทางทวนเข็มนาฬิกาแล้วเดินไปตามเส้นทางที่มีความยาว t
จำนวนลบ t สัมพันธ์กับจุดบนวงกลมหนึ่งหน่วย ซึ่งเราจะไปถึงได้หากเราเคลื่อนที่ไปตามวงกลมจากจุดเริ่มต้นในทิศทางตามเข็มนาฬิกาแล้วเดินไปในเส้นทางที่มีความยาว |t| -

ตอนนี้เรามาดูคำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของจำนวน t สมมติว่าตัวเลข t ตรงกับจุดบนวงกลม A 1 (x, y) (เช่น ตัวเลข &pi/2; ตรงกับจุด A 1 (0, 1))

คำนิยาม.

ไซน์ของจำนวน t คือลำดับของจุดบนวงกลมหนึ่งหน่วยที่ตรงกับเลข t นั่นคือ sint=y

คำนิยาม.

โคไซน์ของจำนวน t เรียกว่าจุดหักของจุดในวงกลมหน่วยซึ่งตรงกับเลข t นั่นคือ cost=x

คำนิยาม.

แทนเจนต์ของจำนวน t คืออัตราส่วนของพิกัดต่อจุดหักมุมของจุดบนวงกลมหนึ่งหน่วยซึ่งสอดคล้องกับตัวเลข t นั่นคือ tgt=y/x ในสูตรที่เทียบเท่ากันอีกสูตรหนึ่ง ค่าแทนเจนต์ของตัวเลข t คืออัตราส่วนของไซน์ของจำนวนนี้ต่อโคไซน์ ซึ่งก็คือ tgt=sint/cost

คำนิยาม.

โคแทนเจนต์ของจำนวน t คืออัตราส่วนของ abscissa ต่อพิกัดของจุดบนวงกลมหนึ่งหน่วยที่สอดคล้องกับตัวเลข t นั่นคือ ctgt=x/y อีกสูตรหนึ่งคือ ค่าแทนเจนต์ของจำนวน t คืออัตราส่วนของโคไซน์ของจำนวน t ต่อไซน์ของจำนวน t: ctgt=cost/sint

ที่นี่เราทราบว่าคำจำกัดความที่เพิ่งให้นั้นสอดคล้องกับคำจำกัดความที่ให้ไว้ตอนต้นของย่อหน้านี้ อันที่จริงจุดบนวงกลมหน่วยที่ตรงกับตัวเลข t เกิดขึ้นพร้อมกับจุดที่ได้จากการหมุนจุดเริ่มต้นเป็นมุม t เรเดียน

มันยังคุ้มค่าที่จะชี้แจงประเด็นนี้ สมมุติว่าเรามีค่า sin3 เราจะเข้าใจได้อย่างไรว่าเรากำลังพูดถึงไซน์ของเลข 3 หรือไซน์ของมุมการหมุนของ 3 เรเดียน? ซึ่งมักจะชัดเจนจากบริบท ไม่เช่นนั้นอาจไม่มีความสำคัญพื้นฐาน

ฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์เชิงมุมและตัวเลข

ตามคำจำกัดความที่ให้ไว้ในย่อหน้าก่อนหน้า แต่ละมุมของการหมุน α สอดคล้องกับค่าsinαที่เฉพาะเจาะจงมาก เช่นเดียวกับค่าcosα นอกจากนี้ มุมการหมุนทั้งหมดที่ไม่ใช่ 90°+180°k, k∈Z (π/2+πk rad) จะสอดคล้องกับค่า tgα และค่าอื่นที่ไม่ใช่ 180°k, k∈Z (πk rad ) – ค่า ของctgα ดังนั้น sinα, cosα, tanα และ ctgα จึงเป็นฟังก์ชันของมุม α กล่าวอีกนัยหนึ่ง สิ่งเหล่านี้คือฟังก์ชันของอาร์กิวเมนต์เชิงมุม

เราสามารถพูดในทำนองเดียวกันเกี่ยวกับฟังก์ชันไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของอาร์กิวเมนต์เชิงตัวเลข แท้จริงแล้ว จำนวนจริง t แต่ละตัวสอดคล้องกับค่า Sin และราคาต้นทุนที่เฉพาะเจาะจงมาก นอกจากนี้ ตัวเลขทั้งหมดที่ไม่ใช่ π/2+π·k, k∈Z จะสอดคล้องกับค่า tgt และตัวเลข π·k, k∈Z - ค่า ctgt

เรียกว่าฟังก์ชันไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ ฟังก์ชันตรีโกณมิติพื้นฐาน.

มักจะชัดเจนจากบริบทว่าเรากำลังเผชิญกับฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์เชิงมุมหรืออาร์กิวเมนต์เชิงตัวเลข มิฉะนั้น เราสามารถมองตัวแปรอิสระว่าเป็นทั้งการวัดมุม (อาร์กิวเมนต์เชิงมุม) และอาร์กิวเมนต์เชิงตัวเลข

อย่างไรก็ตาม ที่โรงเรียนเราศึกษาฟังก์ชันตัวเลขเป็นหลัก นั่นคือ ฟังก์ชันที่มีการโต้แย้งตลอดจนค่าฟังก์ชันที่เกี่ยวข้องเป็นตัวเลข ดังนั้นหากเรากำลังพูดถึงฟังก์ชันโดยเฉพาะ ขอแนะนำให้พิจารณาฟังก์ชันตรีโกณมิติเป็นฟังก์ชันของอาร์กิวเมนต์ตัวเลข

ความสัมพันธ์ระหว่างคำจำกัดความจากเรขาคณิตและตรีโกณมิติ

หากเราพิจารณามุมการหมุน α ที่มีค่าตั้งแต่ 0 ถึง 90 องศา ดังนั้น คำจำกัดความของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของมุมการหมุนในบริบทของตรีโกณมิติจะสอดคล้องกับคำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของ มุมแหลมในรูปสามเหลี่ยมมุมฉาก ซึ่งกำหนดไว้ในหลักสูตรเรขาคณิต เรามาพิสูจน์เรื่องนี้กัน

ลองพรรณนามันเป็นรูปสี่เหลี่ยมผืนผ้า ระบบคาร์ทีเซียนพิกัดวงกลมหน่วยออกซิเจน บันทึก จุดเริ่มก(1, 0) . ลองหมุนเป็นมุม α ตั้งแต่ 0 ถึง 90 องศา เราจะได้จุด A 1 (x, y) ให้เราปล่อยเส้นตั้งฉาก A 1 H จากจุด A 1 ไปยังแกน Ox

เห็นได้ง่ายว่าในรูปสามเหลี่ยมมุมฉาก มุม A 1 OH เท่ากับมุมการหมุน α ความยาวของขา OH ที่อยู่ติดกับมุมนี้จะเท่ากับจุดหักมุมของจุด A 1 นั่นคือ |OH |=x ความยาวของขา A 1 H ตรงข้ามกับมุมเท่ากับพิกัดของจุด A 1 นั่นคือ |A 1 H|=y และความยาวของด้านตรงข้ามมุมฉาก OA 1 เท่ากับ 1 เนื่องจากเป็นรัศมีของวงกลมหนึ่งหน่วย จากนั้น ตามคำนิยามจากเรขาคณิต ไซน์ของมุมแหลม α ในรูปสามเหลี่ยมมุมฉาก A 1 OH เท่ากับอัตราส่วนของขาตรงข้ามต่อด้านตรงข้ามมุมฉาก นั่นคือ sinα=|A 1 H|/|OA 1 |= ปี/1=ปี และตามคำจำกัดความจากตรีโกณมิติ ไซน์ของมุมการหมุน α เท่ากับพิกัดของจุด A 1 นั่นคือ sinα=y นี่แสดงให้เห็นว่าการหาไซน์ของมุมแหลมในรูปสามเหลี่ยมมุมฉากนั้นเทียบเท่ากับการหาไซน์ของมุมการหมุน α เมื่อ α อยู่ระหว่าง 0 ถึง 90 องศา

ในทำนองเดียวกัน แสดงให้เห็นว่าคำจำกัดความของโคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมเฉียบพลัน α นั้นสอดคล้องกับคำจำกัดความของโคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมการหมุน α

บรรณานุกรม.

เรขาคณิต. เกรด 7-9: หนังสือเรียน เพื่อการศึกษาทั่วไป สถาบัน / [ล. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev ฯลฯ] - ฉบับที่ 20 อ.: การศึกษา, 2553. - 384 น.: ป่วย. - ไอ 978-5-09-023915-8.
โปโกเรลอฟ เอ.วี.เรขาคณิต: หนังสือเรียน. สำหรับเกรด 7-9 การศึกษาทั่วไป สถาบัน / A.V. Pogorelov - ฉบับที่ 2 - อ.: การศึกษา, 2544. - 224 หน้า: ป่วย. - ISBN 5-09-010803-X.
พีชคณิตและฟังก์ชันเบื้องต้น: บทช่วยสอนสำหรับนักเรียนชั้นประถมศึกษาปีที่ 9 มัธยม/ E. S. Kochetkov, E. S. Kochetkova; เรียบเรียงโดยดุษฎีบัณฑิตสาขาวิทยาศาสตร์กายภาพและคณิตศาสตร์ O. N. Golovin - ฉบับที่ 4 อ.: การศึกษา, 2512.
พีชคณิต:หนังสือเรียน สำหรับเกรด 9 เฉลี่ย โรงเรียน/ยู N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; เอ็ด S. A. Telyakovsky - ม.: การศึกษา, 2533 - 272 หน้า: ป่วย - ISBN 5-09-002727-7
พีชคณิตและจุดเริ่มต้นของการวิเคราะห์: Proc. สำหรับเกรด 10-11 การศึกษาทั่วไป สถาบัน / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn และคนอื่น ๆ ; เอ็ด A. N. Kolmogorov - ฉบับที่ 14 - ม.: การศึกษา, 2547 - 384 หน้า: ป่วย - ISBN 5-09-013651-3
มอร์ดโควิช เอ.จี.พีชคณิตและจุดเริ่มต้นของการวิเคราะห์ ชั้นประถมศึกษาปีที่ 10 เวลา 14.00 น. ตอนที่ 1: บทช่วยสอนสำหรับ สถาบันการศึกษา(ระดับโปรไฟล์)/ A. G. Mordkovich, P. V. Semenov - ฉบับที่ 4, เสริม. - อ.: Mnemosyne, 2550. - 424 หน้า: ป่วย. ไอ 978-5-346-00792-0.
พีชคณิตและเริ่มต้น การวิเคราะห์ทางคณิตศาสตร์- เกรด 10: หนังสือเรียน เพื่อการศึกษาทั่วไป สถาบัน: พื้นฐานและโปรไฟล์ ระดับ /[Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; แก้ไขโดย เอ.บี. ซิจเชนโก้. - ฉบับที่ 3 - I.: การศึกษา, 2010.- 368 หน้า: ill.- ISBN 978-5-09-022771-1.
บาชมาคอฟ เอ็ม.ไอ.พีชคณิตและจุดเริ่มต้นของการวิเคราะห์: หนังสือเรียน สำหรับเกรด 10-11 เฉลี่ย โรงเรียน - ฉบับที่ 3 - อ.: การศึกษา พ.ศ. 2536 - 351 หน้า: ป่วย - ไอ 5-09-004617-4.
Gusev V.A., Mordkovich A.G.คณิตศาสตร์ (คู่มือสำหรับผู้เข้าโรงเรียนเทคนิค) พรบ. เบี้ยเลี้ยง.- ม.; สูงกว่า โรงเรียน พ.ศ. 2527-351 น. ป่วย

จากกราฟจะชัดเจนว่า:

กราฟไซน์และโคไซน์มีความผันผวนระหว่าง -1 ถึง 1
เส้นโค้งโคไซน์มีรูปร่างเหมือนกับเส้นโค้งไซน์ แต่จะเลื่อนสัมพันธ์กัน 90 o
เส้นโค้งไซน์และโคไซน์มีความต่อเนื่องและวนซ้ำด้วยคาบ 360 o ส่วนเส้นโค้งแทนเจนต์มีความไม่ต่อเนื่องและวนซ้ำด้วยคาบ 180 o

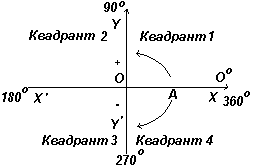ในรูป ทางด้านซ้ายคือแกนตั้งฉาก XX" และ YY"; ตัดกันที่จุดกำเนิดของพิกัด O เมื่อทำงานกับกราฟ การวัดทางขวาและขึ้นจาก O ถือเป็นค่าบวก ทางซ้ายและลงจาก O ถือเป็นค่าลบ ปล่อยให้ OA หมุนได้อย่างอิสระโดยสัมพันธ์กับ O เมื่อหมุน OA ทวนเข็มนาฬิกา มุมที่วัดได้จะถือเป็นมุมบวก และเมื่อหมุนตามเข็มนาฬิกาจะถือว่าเป็นมุมลบ

กำหนดการ. บวกหรือลบ
ทิศทางเมื่อเคลื่อนที่เป็นวงกลม

ให้ OA หมุนทวนเข็มนาฬิกาในลักษณะที่ Θ 1 เป็นมุมใดๆ ในจตุภาคแรก และสร้าง AB ตั้งฉากเพื่อให้ได้ OAB สามเหลี่ยมมุมฉากในรูปที่ 1 ซ้าย. เนื่องจากด้านทั้งสามของรูปสามเหลี่ยมเป็นบวก ฟังก์ชันตรีโกณมิติไซน์ โคไซน์ และแทนเจนต์ในจตุภาคแรกจึงเป็นบวก (โปรดทราบว่าความยาว OA จะเป็นค่าบวกเสมอ เนื่องจากเป็นรัศมีของวงกลม)
ให้ OA หมุนต่อไปในลักษณะที่ Θ 2 คือมุมใดๆ ในจตุภาคที่สอง และสร้าง AC เพื่อให้เกิด OAC สามเหลี่ยมมุมฉาก จากนั้นบาป Θ 2 =+/+ = +; เพราะ Θ 2 =+/- = -; ตาล Θ 2 =+/- = -. ให้ OA หมุนต่อไปในลักษณะที่ Θ 3 คือมุมใดๆ ในจตุภาคที่สาม และสร้าง AD เพื่อให้เกิด OAD สามเหลี่ยมมุมฉาก จากนั้นบาป Θ 3 = -/+ = -; เพราะ Θ 3 = -/+ = -; ตาล Θ 3 = -/- =+

กำหนดการ. การสร้างมุมใน
จตุภาคที่แตกต่างกัน

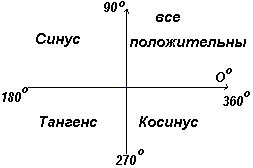ให้ OA หมุนต่อไปในลักษณะที่ Θ 4 เป็นมุมใดๆ ในจตุภาคที่สี่ และสร้าง AE เพื่อให้เกิดสามเหลี่ยมมุมฉาก OAE จากนั้นบาป Θ 4 = -/+= -; เพราะ Θ 4 =+/+=+; ตาล Θ 4 = -/+= -.

ในจตุภาคแรก ฟังก์ชันตรีโกณมิติทั้งหมดจะมีค่าเป็นบวก ในจตุภาคที่สอง เฉพาะไซน์เท่านั้นที่เป็นบวก ในจตุภาคที่สาม เฉพาะแทนเจนต์ ในจตุรัสที่สี่ มีเพียงโคไซน์เท่านั้น ดังแสดงในรูปที่ 1 ซ้าย.

ความรู้เรื่องมุมที่มีขนาดตามอำเภอใจเป็นสิ่งจำเป็นในการค้นหา เช่น ทุกมุมระหว่าง 0 o ถึง 360 o ซึ่งไซน์คือ 0.3261 หากคุณใส่ 0.3261 ลงในเครื่องคิดเลขแล้วกดปุ่ม sin -1 เราจะได้คำตอบ 19.03 o อย่างไรก็ตาม มีมุมที่สองระหว่าง 0 o ถึง 360 o ที่เครื่องคิดเลขจะไม่แสดง ไซน์ก็เป็นบวกเช่นกันในจตุภาคที่สอง อีกมุมหนึ่งแสดงไว้ในรูปที่. ด้านล่างเป็นมุม Θ โดยที่ Θ=180 o - 19.03 o = 160.97 o ดังนั้น 19.03 o และ 160.97 o จึงเป็นมุมที่อยู่ในช่วงตั้งแต่ 0 o ถึง 360 o ซึ่งไซน์คือ 0.3261

ระวัง! เครื่องคิดเลขให้ค่าเหล่านี้เพียงค่าเดียวเท่านั้น ค่าที่สองควรถูกกำหนดตามทฤษฎีมุมโดยพลการ

ตัวอย่างที่ 1

ค้นหามุมทั้งหมดในช่วงตั้งแต่ 0 o ถึง 360 o โดยมีไซน์คือ -0.7071

สารละลาย:
มุมที่มีไซน์เป็น -0.7071 o อยู่ในจตุภาคที่สามและสี่ เนื่องจากไซน์เป็นลบในจตุภาคเหล่านี้ (ดูรูปด้านซ้าย)

กำหนดการ. ค้นหาทุกมุมโดย
ให้ค่าไซน์ (ตัวอย่าง)

จากรูปต่อไปนี้ Θ = arcsin 0.7071 = 45 o มุมสองมุมในช่วงตั้งแต่ 0 o ถึง 360 o ซึ่งมีค่าไซน์คือ -0.7071 คือ 180 o +45 o = 225 o และ 360 o - 45 o = 315 o

บันทึก.เครื่องคิดเลขให้คำตอบเดียวเท่านั้น
กำหนดการ. ค้นหาทุกมุมโดย
ให้ค่าไซน์ (ตัวอย่าง)

ตัวอย่างที่ 2

ค้นหามุมทั้งหมดระหว่าง 0 o ถึง 360 o ซึ่งแทนเจนต์คือ 1.327

สารละลาย:
แทนเจนต์เป็นบวกในจตุภาคที่หนึ่งและสาม - รูปที่ ซ้าย.
กำหนดการ. ค้นหาทุกมุมโดย

จากรูปด้านล่าง Θ = arctan1.327= 53 o
มุมสองมุมในช่วงตั้งแต่ 0 o ถึง 360 o ซึ่งแทนเจนต์คือ 1.327 คือ 53 o และ 180 o + 53 o เช่น 233 โอ
กำหนดการ. ค้นหาทุกมุมโดย
ให้ค่าแทนเจนต์ (ตัวอย่าง)

ให้หรือในรูป ทางด้านซ้ายเป็นเวกเตอร์ของความยาวหน่วย ซึ่งหมุนทวนเข็มนาฬิกาอย่างอิสระรอบ O การปฏิวัติหนึ่งครั้งทำให้เกิดวงกลมดังแสดงในรูปที่ 1 และแบ่งออกเป็นภาค 15 o แต่ละรัศมีมีองค์ประกอบแนวนอนและแนวตั้ง ตัวอย่างเช่น สำหรับ 30 o องค์ประกอบแนวตั้งคือ TS และองค์ประกอบแนวนอนคือ OS

จากนิยามของฟังก์ชันตรีโกณมิติ
sin30 o =TS/TO=TS/1 เช่น TS= บาป30 oและ cos30 o =OS/TO=OS/1 เช่น ระบบปฏิบัติการ=cos30 o

องค์ประกอบแนวตั้ง TS สามารถพล็อตเป็น T"S" ซึ่งเท่ากับค่าที่สอดคล้องกับมุม 30 o บนกราฟของ y กับมุม x หากส่วนประกอบแนวตั้งทั้งหมด เช่น TS ถูกถ่ายโอนไปยังกราฟ คุณจะได้ไซนูซอยด์ดังแสดงในรูปที่ 1 สูงกว่า

หากองค์ประกอบแนวนอนทั้งหมด เช่น OS ถูกฉายลงบนกราฟ y กับมุม x ผลลัพธ์ที่ได้คือคลื่นโคไซน์ เส้นโครงเหล่านี้สามารถมองเห็นได้ง่ายโดยการวาดวงกลมที่มีรัศมี OR และมุมที่เกิดจากแนวตั้ง ดังแสดงในรูปด้านซ้าย
จากรูป ทางด้านซ้ายจะเห็นว่าคลื่นไซน์มีรูปร่างเหมือนกับคลื่นโคไซน์ แต่เลื่อนไปทาง 90 o

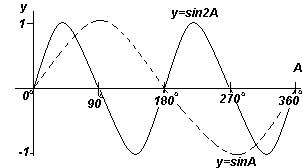ฟังก์ชันคาบและคาบ
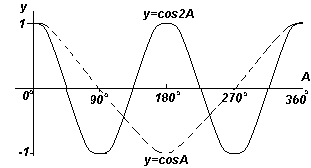
กราฟฟังก์ชันแต่ละกราฟที่แสดงในรูปที่สี่ ด้านบน จะถูกทำซ้ำเมื่อมุม A เพิ่มขึ้น ซึ่งเป็นสาเหตุว่าทำไมจึงถูกเรียกว่า ฟังก์ชันเป็นระยะ.
ฟังก์ชัน y=sinA และ y=cosA จะถูกทำซ้ำทุกๆ 360 o (หรือ 2π เรเดียน) ดังนั้น 360 o จึงถูกเรียกว่า ระยะเวลาฟังก์ชั่นเหล่านี้ ฟังก์ชัน y=sin2A และ y=cos2A จะถูกทำซ้ำทุกๆ 180 o (หรือ π เรเดียน) ดังนั้น 180 o คือคาบสำหรับฟังก์ชันเหล่านี้
โดยทั่วไป ถ้า y=sinpA และ y=cospA (โดยที่ p เป็นค่าคงที่) คาบของฟังก์ชันจะเป็น 360 o /p (หรือ 2π/p เรเดียน) ดังนั้น หาก y=sin3A คาบของฟังก์ชันนี้จะเท่ากับ 360 o /3= 120 o ถ้า y=cos4A คาบของฟังก์ชันนี้จะเท่ากับ 360 o /4= 90 o

แอมพลิจูด
แอมพลิจูดเรียกว่าค่าสูงสุดของไซนัสอยด์ กราฟ 1-4 แต่ละกราฟมีแอมพลิจูดเป็น +1 (นั่นคือ กราฟจะผันผวนระหว่าง +1 ถึง -1) อย่างไรก็ตาม หาก y=4sinA แต่ละค่า sinA จะถูกคูณด้วย 4 ดังนั้นค่าแอมพลิจูดสูงสุดคือ 4 ในทำนองเดียวกันสำหรับ y=5cos2A แอมพลิจูดคือ 5 และคาบคือ 360 o /2 = 180 o

ตัวอย่างที่ 3
สร้าง y=3sin2A ในช่วงตั้งแต่ A=0 o ถึง A=360 o

สารละลาย:
แอมพลิจูด =3, คาบ = 360 o /2 =180 o

ตัวอย่างที่ 4
วาดกราฟของ y=4cos2x ในช่วงตั้งแต่ x=0 o ถึง x=360 o

สารละลาย:
แอมพลิจูด = 4. คาบ = 360 o /2 = 180 o

มุมของความล่าช้าและความก้าวหน้า
เส้นโค้งไซน์และโคไซน์ไม่ได้เริ่มต้นที่ 0 เสมอไป เพื่อคำนึงถึงข้อเท็จจริงนี้ ฟังก์ชั่นเป็นระยะแสดงเป็น y=sin(A± α) โดยที่ α คือการเปลี่ยนเฟสสัมพันธ์กับ y=sinA และ y=cosA

เมื่อรวบรวมตารางค่าแล้ว คุณสามารถสร้างกราฟของฟังก์ชัน y=sin(A-60 o) ดังแสดงในรูปที่ 1 ซ้าย. หากเส้นโค้ง y=sinA เริ่มต้นที่ 0 o ดังนั้นเส้นโค้ง y=sin(A-60 o) เริ่มต้นที่ 60 o (กล่าวคือ ค่าศูนย์คือ 60 o ทางด้านขวา) ดังนั้นพวกเขาจึงกล่าวว่า y=sin(A-60 o) สายแล้วสัมพันธ์กับ y=sinA คูณ 60 o
กำหนดการ. y=sin(A-60 o) (ไซนูซอยด์)

ด้วยการรวบรวมตารางค่า คุณสามารถสร้างกราฟของฟังก์ชัน y=cos(A+45 o) ดังแสดงในรูปที่ 1 ด้านล่าง.
หากเส้นโค้ง y=cosA เริ่มต้นที่ 0 o ดังนั้นเส้นโค้ง y=cos(A+45 o) จะเริ่มต้นที่ 45 o ไปทางซ้าย (กล่าวคือ ค่าศูนย์คือ 45 o ก่อนหน้า)
ดังนั้นกราฟจึงเรียกว่า y=cos(A+45 o) ข้างหน้ากราฟ y=cosA ที่ 45 o
กำหนดการ. y=cos(A+45 o) (คลื่นโคไซน์)

โดยทั่วไป กราฟ y=sin(A-α) จะล่าช้าสัมพันธ์กับ y=sinA ตามมุม α
คลื่นโคไซน์มีรูปร่างเหมือนกับคลื่นไซน์ แต่เริ่มต้นที่ 90 o ไปทางซ้าย นั่นคือ ข้างหน้าเธอ 90 โมง ดังนั้น cosA=sin(A+90 o)

ตัวอย่างที่ 5
วาดกราฟ y=5sin(A+30 o) ในช่วงตั้งแต่ A=0 o ถึง A=360 o

สารละลาย:
แอมพลิจูด = 5, คาบ = 360 o /1 = 360 o
5sin(A+30 o) นำหน้า 5sinA 30 o เช่น เริ่ม 30 o เร็วกว่านั้น
กราฟ y=5sin(A+30 o) (ไซนัสอยด์)

ตัวอย่างที่ 6
วาดกราฟ y=7sin(2A-π/3) ในช่วงตั้งแต่ A=0 o ถึง A=360 o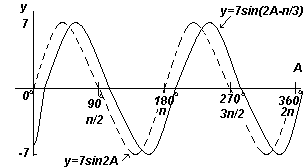

สารละลาย:
แอมพลิจูด = 7, คาบ =2π/2= π เรเดียน
โดยทั่วไปแล้ว y=sin(pt-α) ล่าช้าสัมพันธ์กับ y=sinpt โดย α/pดังนั้น 7sin(2A-π/3) จึงช้ากว่า 7sin2A โดย (π/3)/2 กล่าวคือ โดย π/6 เรเดียน หรือ 30 o

ไซนูซอยด์ในรูปแบบ Asin(ωt±α) มุมเฟส การเปลี่ยนเฟส

ให้หรือในรูป ทางด้านซ้ายเป็นเวกเตอร์ที่หมุนทวนเข็มนาฬิกาอย่างอิสระรอบ O ด้วยความเร็ว ω เรเดียน/วินาที เรียกว่าเวกเตอร์ที่กำลังหมุน เวกเตอร์เฟส- หลังจากเวลาผ่านไป t วินาที OR จะหมุนเป็นมุม ωt เรเดียน (ในรูปด้านซ้ายคือมุม TOR) ถ้าเราสร้าง ST ตั้งฉากกับ OR แล้ว sinωt=ST/OT เช่น ST=OTซินωt.
หากองค์ประกอบแนวตั้งทั้งหมดถูกฉายลงบนกราฟ y เทียบกับ ωt จะได้ไซนัสอยด์ที่มีแอมพลิจูด OR

ถ้าเวกเตอร์เฟส OR ทำการปฏิวัติหนึ่งครั้ง (เช่น 2π เรเดียน) ในหน่วย T วินาที แล้วความเร็วเชิงมุม ω=2π/T rad/s ดังนั้น
T=2π/ ω (s) โดยที่
ทีคือ ระยะเวลา
เรียกว่าจำนวนคาบที่สมบูรณ์ที่ผ่านไปใน 1 วินาที ความถี่ฉ.
ความถี่ = (จำนวนคาบ)/(วินาที) = 1/ T = ω/2π Hz,เหล่านั้น. ฉ= ω/2π เฮิรตซ์
ดังนั้นความเร็วเชิงมุม
ω=2πf ราด/วินาที

หากโดยทั่วไปแล้วฟังก์ชันไซน์ซอยด์ดูเหมือน y=sin(ωt± α) แล้ว
เอ - แอมพลิจูด
ω - ความเร็วเชิงมุม
2π/ ω - คาบ T, s
ω/2π - ความถี่ f, Hz
α คือมุมก้าวหน้าหรือมุมหน่วง (สัมพันธ์กับ y=Аsinωt) ในหน่วยเรเดียน เรียกอีกอย่างว่ามุมเฟส

ตัวอย่างที่ 7
กระแสสลับกำหนดเป็น i=20sin(90πt+0.26) แอมแปร์ กำหนดแอมพลิจูด คาบ ความถี่ และมุมเฟส (เป็นองศา)

สารละลาย:
i=20sin(90πt+0.26)ดังนั้น
แอมพลิจูดคือ 20 ก
ความเร็วเชิงมุม ω=90π ดังนั้น
ช่วง T= 2π/ ω = 2π/ 90π = 0.022 วินาที = 22ms
ความถี่ ฉ= 1/T = 1/0.022 = 45.46 เฮิรตซ์
มุมเฟส α= 0.26 ราด = (0.26*180/π) o = 14.9 o

ตัวอย่างที่ 8
กลไกการสั่นมีระยะกระจัดสูงสุด 3 ม. และความถี่ 55 Hz ที่เวลา t=0 การกระจัดคือ 100 ซม. แสดงการกระจัดในรูปแบบทั่วไป Аsin(ωt± α)

สารละลาย
แอมพลิจูด = การกระจัดสูงสุด = 3m
ความเร็วเชิงมุม ω=2πf = 2π(55) = 110 πrad/s
ดังนั้นการกระจัดคือ 3sin(110πt + α) m
ที่ระยะการกระจัด t=0 = 100ซม.=1ม.
ดังนั้น 1= 3sin(0 + α) เช่น ซินα=1/3=0.33
ดังนั้น α=อาร์คซิน0.33=19 o
ดังนั้นออฟเซ็ตคือ 3sin(110 πt + 0.33)

ตัวอย่างที่ 9
ค่าของแรงดันไฟฟ้าชั่วขณะในวงจรไฟฟ้ากระแสสลับที่ t วินาทีใดๆ จะได้รับเป็น v=350sin(40πt-0.542)V หา:
ก) แอมพลิจูด คาบ ความถี่ และมุมเฟส (เป็นองศา)
b) ค่าแรงดันไฟฟ้าที่ t =0
c) ค่าแรงดันไฟฟ้าที่ t = 10 ms
d) เวลาที่แรงดันไฟฟ้าถึง 200 V ครั้งแรก
สารละลาย:
ก) แอมพลิจูดคือ 350 V ความเร็วเชิงมุมคือ ω=40π
เพราะฉะนั้น,
ระยะเวลา T=2π/ ω=2π/40π=0.05 วินาที =50ms
ความถี่ f=1/T=1/0.05=20 เฮิรตซ์
มุมเฟส = 0.542 rad (0.542*180/π) = 31 o โดยมีความล่าช้าสัมพันธ์กับ v=350sin(40πt)
b) ถ้า t =0 ดังนั้น v=350sin(0-0.542)=350sin(-31 o)=-180.25 V
c) ถ้า t =10 ms ดังนั้น v=350sin(40π10/10 3 -0.542)=350sin(0.714)=350sin41 o =229.6 V
d) ถ้า v=200 I แล้ว 200=350sin(40πt-0.542) 200/350=sin(40πt-0.542)

กำหนดการ. กลไกการสั่น
(ตัวอย่างคลื่นไซน์)

v=350sin(40πt-0.542) ดังนั้น (40πt-0.542)=อาร์คซิน200/350=35 o หรือ 0.611 rad
40πt= 0.611+0.542=1.153
ดังนั้น ถ้า v=200V แล้ว เวลา t=1.153/40π=9.179 ms

คำจำกัดความทางเรขาคณิตของไซน์และโคไซน์

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α - มุมแสดงเป็นเรเดียน

ไซน์ (บาป α)เป็นฟังก์ชันตรีโกณมิติของมุม α ระหว่างด้านตรงข้ามมุมฉากกับขาของรูปสามเหลี่ยมมุมฉาก เท่ากับอัตราส่วนของความยาวของขาตรงข้าม |BC| เท่ากับความยาวของด้านตรงข้ามมุมฉาก |AB|

โคไซน์ (คอส α)เป็นฟังก์ชันตรีโกณมิติของมุม α ระหว่างด้านตรงข้ามมุมฉากกับขาของรูปสามเหลี่ยมมุมฉาก เท่ากับอัตราส่วนของความยาวของขาที่อยู่ติดกัน |AC| เท่ากับความยาวของด้านตรงข้ามมุมฉาก |AB|

นิยามตรีโกณมิติ

เมื่อใช้สูตรข้างต้น คุณจะพบไซน์และโคไซน์ของมุมแหลมได้ แต่คุณต้องเรียนรู้วิธีคำนวณไซน์และโคไซน์ของมุมที่มีขนาดใดก็ได้ สามเหลี่ยมมุมฉากไม่ได้ให้โอกาสดังกล่าว (เช่น ไม่สามารถมีมุมป้านได้) ดังนั้นจึงจำเป็นต้องมีมากกว่านี้ คำจำกัดความทั่วไปไซน์และโคไซน์ที่มีสูตรระบุเป็นกรณีพิเศษ

วงกลมตรีโกณมิติมาช่วย ปล่อยให้มีมุมบ้าง มันตรงกับจุดที่มีชื่อเดียวกันบนวงกลมตรีโกณมิติ

ข้าว. 2. นิยามตรีโกณมิติของไซน์และโคไซน์

โคไซน์ของมุมคือค่าแอบซิสซาของจุด ไซน์ของมุมคือพิกัดของจุด

ในรูป 2 มุมนั้นแหลมและเข้าใจได้ง่าย คำจำกัดความนี้ตรงกับเรื่องทั่วไป คำจำกัดความทางเรขาคณิต- ที่จริงแล้ว เราเห็นสามเหลี่ยมมุมฉากซึ่งมีหน่วยด้านตรงข้ามมุมฉาก O และมุมแหลม ขาที่อยู่ติดกันของสามเหลี่ยมนี้คือ cos (เปรียบเทียบกับรูปที่ 1) และในเวลาเดียวกัน abscissa ของจุด ด้านตรงข้ามคือบาป (ดังรูปที่ 1) และในขณะเดียวกันก็เป็นลำดับของจุด

แต่ตอนนี้เราไม่ได้ถูกจำกัดโดยไตรมาสแรกอีกต่อไปแล้ว และมีโอกาสที่จะขยายคำจำกัดความนี้ไปในทุกมุม ในรูป รูปที่ 3 แสดงค่าไซน์และโคไซน์ของมุมในไตรมาสที่ 2, 3 และ 4

ข้าว. 3. ไซน์และโคไซน์ในไตรมาสที่ II, III และ IV

ค่าตารางของไซน์และโคไซน์

มุมศูนย์ \(\LARGE 0^(\circ ) \)

พิกัดของจุด 0 เท่ากับ 1 พิกัดของจุด 0 เท่ากับ 0 เพราะฉะนั้น,

เพราะ 0 = 1 บาป 0 = 0

รูปที่ 4 มุมเป็นศูนย์

มุม \(\LARGE \frac(\pi)(6) = 30^(\circ )\)

เราเห็นสามเหลี่ยมมุมฉากซึ่งมีหน่วยด้านตรงข้ามมุมฉากและมีมุมแหลม 30° ดังที่คุณทราบ ขาที่วางตรงข้ามกับมุม 30° เท่ากับครึ่งหนึ่งของด้านตรงข้ามมุมฉาก 1 กล่าวอีกนัยหนึ่งขาแนวตั้งมีค่าเท่ากับ 1/2 ดังนั้น

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

เราหาขาแนวนอนโดยใช้ทฤษฎีบทของพีทาโกรัส (หรือที่เหมือนกัน คือ เราหาโคไซน์โดยใช้อัตลักษณ์ตรีโกณมิติพื้นฐาน):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 )\]

1 ทำไมสิ่งนี้ถึงเกิดขึ้น? ตัดสามเหลี่ยมด้านเท่าโดยให้ด้าน 2 เรียงตามความสูง! มันจะแบ่งออกเป็นสามเหลี่ยมมุมฉากสองอัน โดยมีด้านตรงข้ามมุมฉากเป็น 2, มุมแหลมเป็น 30° และด้านสั้นกว่าเป็น 1

รูปที่ 5 มุม π / 6

มุม \(\LARGE \frac(\pi)(4) = 45^(\circ )\)

ในกรณีนี้ สามเหลี่ยมมุมฉากคือหน้าจั่ว ไซน์และโคไซน์ของมุม 45° มีค่าเท่ากัน ให้เราแสดงพวกมันด้วย x ในตอนนี้ เรามี:

\[ x^(2) + x^(2) = 1 \]

โดยที่ \(x=\frac(\sqrt(2) )(2) \) เพราะฉะนั้น,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

รูปที่ 5 มุม π/4

คุณสมบัติของไซน์และโคไซน์

สัญกรณ์ที่ยอมรับ

\(\sin^2 x \equiv (\sin x)^2; \)\(\รูปสี่เหลี่ยม \sin^3 x \equiv (\sin x)^3; \)\(\รูปสี่เหลี่ยม \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\รูปสี่เหลี่ยม \cos^3 x \equiv (\cos x)^3; \)\(\รูปสี่เหลี่ยม \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

ความเป็นงวด

ฟังก์ชัน y = sin x และ y = cos x มีคาบโดยมีคาบ 2π

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

ความเท่าเทียมกัน

ฟังก์ชันไซน์เป็นเลขคี่ ฟังก์ชันโคไซน์เป็นเลขคู่

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

พื้นที่ของคำจำกัดความและค่านิยม สุดโต่ง การเพิ่มขึ้น การลดลง

คุณสมบัติพื้นฐานของไซน์และโคไซน์แสดงอยู่ในตาราง ( n- ทั้งหมด).

	\(\เล็ก< x < \)	\(\small -\pi + 2\pi n \) \(\small< x < \) \(\small 2\pi n \)
จากมากไปน้อย	\(\small \dfrac(\pi)2 + 2\pi n \)\(\เล็ก< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \)	\(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \)
แม็กซิมา \(\เล็ก x = \) \(\small \dfrac(\pi)2 + 2\pi n \)	\(\เล็ก x = 2\ไพ n\)
ขั้นต่ำ, \(\เล็ก x = \) \(\small -\dfrac(\pi)2 + 2\pi n \)	\(\small x = \) \(\small \pi + 2\pi n \)
ศูนย์, \(\small x = \pi n\)	\(\small x = \dfrac(\pi)2 + \pi n \)
จุดตัดของแกน Y, x = 0	ย = 0	ย = 1

สูตรพื้นฐานที่มีไซน์และโคไซน์

ผลรวมของกำลังสอง

\(\บาป^2 x + \cos^2 x = 1\)

สูตรไซน์และโคไซน์สำหรับผลรวมและผลต่าง

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

สูตรผลคูณของไซน์และโคไซน์

\(\บาป x \cos y = \) \(\dfrac12 (\ขนาดใหญ่ [) \sin(x - y) + \sin(x + y) (\ขนาดใหญ่ ]) \)
\(\บาป x \บาป y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\ใหญ่ [) 1 - \cos 2x (\ใหญ่ ]) \)
\(\cos^2 x = \dfrac12 (\ขนาดใหญ่ [) 1 + \cos 2x (\ขนาดใหญ่ ]) \)

สูตรผลรวมและผลต่าง

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

แสดงไซน์ผ่านโคไซน์

\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\บาป^2 x = 1 - \cos^2 x\) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

แสดงโคไซน์ผ่านไซน์

\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

การแสดงออกผ่านแทนเจนต์

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

ที่ \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

ที่ \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

ตารางไซน์และโคไซน์ แทนเจนต์และโคแทนเจนต์

ตารางนี้แสดงค่าของไซน์และโคไซน์สำหรับค่าหนึ่งของอาร์กิวเมนต์
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="ตารางไซน์และโคไซน์" title="ตารางไซน์และโคไซน์" ]!}

การแสดงออกผ่านตัวแปรที่ซับซ้อน

\(ผม^2 = -1\)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

สูตรของออยเลอร์

\(e^(iz) = \cos z + i \sin z \)

นิพจน์ผ่านฟังก์ชันไฮเปอร์โบลิก

\(\sin iz = ฉัน \sh z \) \(\cos iz = \ch z \)
\(\sh iz = ฉัน \sin z \) \(\ch iz = \cos z \)

อนุพันธ์

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) การหาสูตร > > >

อนุพันธ์ของลำดับที่ n:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).

ปริพันธ์

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
ดูเพิ่มเติมที่ส่วนตารางอินทิกรัลไม่ จำกัด >>>

การขยายซีรีส์

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

เซแคนต์, โคซีแคนต์

\(\วินาที x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

ฟังก์ชันผกผัน

ฟังก์ชันผกผันของไซน์และโคไซน์คืออาร์คไซน์และอาร์กโคไซน์ตามลำดับ

อาร์คซิน, อาร์คซิน

\(y = \อาร์คซิน x\) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\อาร์คซิน x) = x\)
\(\อาร์คซิน(\บาป x) = x\) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)

อาร์คโคไซน์ อาร์คคอส

\(y = \อาร์คคอส x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\อาร์คคอส x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\อาร์คคอส(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

อ้างอิง:
ใน. บรอนสไตน์ เค.เอ. Semendyaev คู่มือคณิตศาสตร์สำหรับวิศวกรและนักศึกษา "Lan", 2552

Javascript ถูกปิดใช้งานในเบราว์เซอร์ของคุณ
หากต้องการคำนวณ คุณต้องเปิดใช้งานตัวควบคุม ActiveX!

ศูนย์กลางอยู่ที่จุด A
α คือมุมที่แสดงเป็นเรเดียน

แทนเจนต์ ( สีแทน α) เป็นฟังก์ชันตรีโกณมิติ ขึ้นอยู่กับมุม α ระหว่างด้านตรงข้ามมุมฉากกับขาของรูปสามเหลี่ยมมุมฉาก เท่ากับอัตราส่วนความยาวของขาตรงข้าม |BC| ไปจนถึงความยาวของขาที่อยู่ติดกัน |AB| -

โคแทนเจนต์ ( ซีทีจี แอลฟา) เป็นฟังก์ชันตรีโกณมิติ ขึ้นอยู่กับมุม α ระหว่างด้านตรงข้ามมุมฉากกับขาของรูปสามเหลี่ยมมุมฉาก เท่ากับอัตราส่วนของความยาวของขาที่อยู่ติดกัน |AB| ถึงความยาวของขาตรงข้าม |BC| -

แทนเจนต์

ที่ไหน n- ทั้งหมด.

ในวรรณคดีตะวันตก แทนเจนต์แสดงดังนี้:
.
;
;
.

กราฟของฟังก์ชันแทนเจนต์ y = tan x

โคแทนเจนต์

ที่ไหน n- ทั้งหมด.

ในวรรณคดีตะวันตก โคแทนเจนต์แสดงดังนี้:
.
ยอมรับสัญลักษณ์ต่อไปนี้ด้วย:
;
;
.

กราฟของฟังก์ชันโคแทนเจนต์ y = ctg x

คุณสมบัติของแทนเจนต์และโคแทนเจนต์

ความเป็นงวด

ฟังก์ชัน y = ทีจีเอ็กซ์และ ย = ซีทีจี xเป็นคาบกับคาบ π

ความเท่าเทียมกัน

ฟังก์ชันแทนเจนต์และโคแทนเจนต์เป็นเลขคี่

พื้นที่ของความหมายและค่านิยม การเพิ่มขึ้น การลดลง

ฟังก์ชันแทนเจนต์และโคแทนเจนต์มีความต่อเนื่องในขอบเขตของคำจำกัดความ (ดูข้อพิสูจน์ความต่อเนื่อง) คุณสมบัติหลักของแทนเจนต์และโคแทนเจนต์แสดงอยู่ในตาราง ( n- ทั้งหมด).

	ย= ทีจีเอ็กซ์	ย= ซีทีจี x
ขอบเขตและความต่อเนื่อง
ช่วงของค่า	-∞ < y < +∞	-∞ < y < +∞
เพิ่มขึ้น		-
จากมากไปน้อย	-
สุดขั้ว	-	-
ศูนย์, y = 0
จุดตัดกับแกนพิกัด x = 0	ย= 0	-

สูตร

นิพจน์โดยใช้ไซน์และโคไซน์

; ;
; ;
;

สูตรแทนเจนต์และโคแทนเจนต์จากผลรวมและผลต่าง

สูตรที่เหลือก็หาได้ง่ายเช่นกัน

ผลคูณของแทนเจนต์

สูตรหาผลรวมและผลต่างของแทนเจนต์

ตารางนี้แสดงค่าแทนเจนต์และโคแทนเจนต์สำหรับค่าบางค่าของการโต้แย้ง

นิพจน์ที่ใช้จำนวนเชิงซ้อน

นิพจน์ผ่านฟังก์ชันไฮเปอร์โบลิก

;
;

อนุพันธ์

; .

.
อนุพันธ์ของลำดับที่ n เทียบกับตัวแปร x ของฟังก์ชัน:
.
การหาสูตรแทนเจนต์ > > > ; สำหรับโคแทนเจนต์ > > >

ปริพันธ์

การขยายซีรีส์

เพื่อให้ได้การขยายตัวของแทนเจนต์ในกำลังของ x คุณต้องใช้เงื่อนไขหลายประการในการขยายอนุกรมกำลังสำหรับฟังก์ชัน บาป xและ เพราะ xและหารพหุนามเหล่านี้ด้วยตัวอื่นๆ สิ่งนี้จะสร้างสูตรต่อไปนี้

ที่ .

ที่ .
ที่ไหน บีเอ็น- หมายเลขเบอร์นูลลี โดยพิจารณาจากความสัมพันธ์ที่เกิดซ้ำ:
;
;
ที่ไหน .
หรือตามสูตรของลาปลาซ:

ฟังก์ชันผกผัน

ฟังก์ชันผกผันของแทนเจนต์และโคแทนเจนต์คืออาร์กแทนเจนต์และอาร์กโคแทนเจนต์ตามลำดับ

อาร์กแทนเจนต์, อาร์กจี

, ที่ไหน n- ทั้งหมด.

อาร์กโคแทนเจนต์, อาร์กซีจี

, ที่ไหน n- ทั้งหมด.

อ้างอิง:
ใน. บรอนสไตน์ เค.เอ. Semendyaev คู่มือคณิตศาสตร์สำหรับวิศวกรและนักศึกษา "Lan", 2552
G. Korn, คู่มือคณิตศาสตร์สำหรับนักวิทยาศาสตร์และวิศวกร, 2012.

อยู่ตรงกลางจุดหนึ่ง ก.
α - มุมแสดงเป็นเรเดียน

คำนิยาม
ไซน์ (บาป α)เป็นฟังก์ชันตรีโกณมิติ ขึ้นอยู่กับมุม α ระหว่างด้านตรงข้ามมุมฉากกับขาของรูปสามเหลี่ยมมุมฉาก เท่ากับอัตราส่วนความยาวของขาตรงข้าม |BC| ความยาวของด้านตรงข้ามมุมฉาก |AC|

โคไซน์ (คอส α)เป็นฟังก์ชันตรีโกณมิติ ขึ้นอยู่กับมุม α ระหว่างด้านตรงข้ามมุมฉากกับขาของรูปสามเหลี่ยมมุมฉาก เท่ากับอัตราส่วนของความยาวของขาที่อยู่ติดกัน |AB| ความยาวของด้านตรงข้ามมุมฉาก |AC|

สัญกรณ์ที่ยอมรับ

;
;
.

กราฟของฟังก์ชันไซน์ y = sin x

กราฟของฟังก์ชันโคไซน์ y = cos x

คุณสมบัติของไซน์และโคไซน์

ความเป็นงวด

ฟังก์ชัน y = บาป xและ ย = เพราะ xเป็นระยะกับช่วงเวลา 2π.

ความเท่าเทียมกัน

ฟังก์ชันไซน์เป็นเลขคี่ ฟังก์ชันโคไซน์เป็นเลขคู่

ขอบเขตของคำจำกัดความและค่านิยม สุดขั้ว เพิ่ม ลด

ฟังก์ชันไซน์และโคไซน์มีความต่อเนื่องในโดเมนของคำจำกัดความ กล่าวคือ สำหรับ x ทั้งหมด (ดูข้อพิสูจน์ความต่อเนื่อง) คุณสมบัติหลักแสดงอยู่ในตาราง (n - จำนวนเต็ม)

	ย= บาป x	ย= เพราะ x
ขอบเขตและความต่อเนื่อง	- ∞ < x < + ∞	- ∞ < x < + ∞
ช่วงของค่า	-1 ≤ ย ≤ 1	-1 ≤ ย ≤ 1
เพิ่มขึ้น
จากมากไปน้อย
แม็กซิมา, y = 1
ขั้นต่ำ, y = - 1
ศูนย์, y = 0
จุดตัดกับแกนพิกัด x = 0	ย= 0	ย= 1

สูตรพื้นฐาน

ผลรวมของกำลังสองของไซน์และโคไซน์

สูตรไซน์และโคไซน์จากผลรวมและผลต่าง

;
;

สูตรผลคูณของไซน์และโคไซน์

สูตรผลรวมและผลต่าง

แสดงไซน์ผ่านโคไซน์

;
;
;
.

แสดงโคไซน์ผ่านไซน์

;
;
;
.

การแสดงออกผ่านแทนเจนต์

; .

เมื่อใด เรามี:
; .

ที่ :
; .

ตารางไซน์และโคไซน์ แทนเจนต์และโคแทนเจนต์

ตารางนี้แสดงค่าของไซน์และโคไซน์สำหรับค่าหนึ่งของอาร์กิวเมนต์

การแสดงออกผ่านตัวแปรที่ซับซ้อน

;

สูตรของออยเลอร์

นิพจน์ผ่านฟังก์ชันไฮเปอร์โบลิก

;
;

อนุพันธ์

อนุพันธ์ของลำดับที่ n:
{ -∞ < x < +∞ }