Lastnosti sinusa in njegovega grafa. Lastnosti sinusa, kosinusa, tangensa in kotangensa

V tem članku bomo pokazali, kako dati definicije sinusa, kosinusa, tangensa in kotangensa kota in števila v trigonometriji. Tukaj bomo govorili o notacijah, podali primere vnosov in podali grafične ponazoritve. Za zaključek naj potegnemo vzporednico med definicijami sinusa, kosinusa, tangensa in kotangensa v trigonometriji in geometriji.

Navigacija po straneh.

Definicija sinusa, kosinusa, tangensa in kotangensa

Poglejmo, kako se v šolskem tečaju matematike oblikuje ideja sinusa, kosinusa, tangensa in kotangensa. Pri pouku geometrije je podana definicija sinusa, kosinusa, tangensa in kotangensa ostrega kota v pravokotnem trikotniku. In kasneje se preučuje trigonometrija, ki govori o sinusu, kosinusu, tangensu in kotangensu kota zasuka in številu. Naj predstavimo vse te definicije, navedemo primere in podamo potrebne komentarje.

Ostri kot v pravokotnem trikotniku

Iz predmeta geometrija poznamo definicije sinusa, kosinusa, tangensa in kotangensa ostrega kota v pravokotnem trikotniku. Podane so kot razmerje stranic pravokotni trikotnik. Naj podamo njihove formulacije.

Opredelitev.

Sinus ostrega kota v pravokotnem trikotniku je razmerje med nasprotno stranico in hipotenuzo.

Opredelitev.

Kosinus ostrega kota v pravokotnem trikotniku je razmerje med sosednjim krakom in hipotenuzo.

Opredelitev.

Tangenta ostrega kota v pravokotnem trikotniku– to je razmerje med nasprotno stranjo in sosednjo stranjo.

Opredelitev.

Kotangens ostrega kota v pravokotnem trikotniku- to je razmerje med sosednjo in nasprotno stranjo.

Tam so uvedene tudi oznake za sinus, kosinus, tangens in kotangens - sin, cos, tg oziroma ctg.

Na primer, če je ABC pravokotni trikotnik s pravim kotom C, potem je sinus ostrega kota A enak razmerju med nasprotno stranjo BC in hipotenuzo AB, to je sin∠A=BC/AB.

Te definicije vam omogočajo, da izračunate vrednosti sinusa, kosinusa, tangensa in kotangensa ostrega kota iz znanih dolžin strani pravokotnega trikotnika, pa tudi iz znanih vrednosti sinusa, kosinusa, tangensa, kotangens in dolžino ene od stranic, da bi našli dolžine drugih stranic. Na primer, če bi vedeli, da je v pravokotnem trikotniku krak AC enak 3 in hipotenuza AB enaka 7, potem bi lahko izračunali vrednost kosinusa ostrega kota A po definiciji: cos∠A=AC/ AB=3/7.

Kot vrtenja

V trigonometriji začnejo na kot gledati širše – uvedejo pojem rotacijski kot. Velikost rotacijskega kota za razliko od ostrega kota ni omejena na 0 do 90 stopinj, rotacijski kot v stopinjah (in v radianih) je lahko izražen s poljubnim realnim številom od −∞ do +∞.

V tej luči so definicije sinusa, kosinusa, tangensa in kotangensa podane ne za ostri kot, temveč za kot poljubne velikosti - kot zasuka. Podane so s koordinatama x in y točke A 1, v katero gre tako imenovana izhodiščna točka A(1, 0) po vrtenju za kot α okoli točke O - začetka pravokotnega kartezičnega koordinatnega sistema. in središče enotskega kroga.

Opredelitev.

Sinus rotacijskega kotaα je ordinata točke A 1, to je sinα=y.

Opredelitev.

Kosinus rotacijskega kotaα imenujemo abscisa točke A 1, to je cosα=x.

Opredelitev.

Tangens kota vrtenjaα je razmerje med ordinato točke A 1 in njeno absciso, to je tanα=y/x.

Opredelitev.

Kotangens rotacijskega kotaα je razmerje med absciso točke A 1 in njeno ordinato, to je ctgα=x/y.

Sinus in kosinus sta definirana za vsak kot α, saj lahko vedno določimo absciso in ordinato točke, ki jo dobimo z vrtenjem izhodišča za kot α. Toda tangens in kotangens nista definirana za noben kot. Tangenta ni definirana za kote α, pri katerih gre začetna točka v točko z ničelno absciso (0, 1) ali (0, −1), in to se zgodi pri kotih 90°+180° k, k∈Z (π /2+π·k rad). Dejansko pri takšnih kotih vrtenja izraz tgα=y/x nima smisla, saj vsebuje deljenje z nič. Kar zadeva kotangens, ni definiran za kote α, pri katerih gre začetna točka v točko z ničelno ordinato (1, 0) ali (−1, 0), in to se zgodi za kote 180° k, k ∈Z (π·k rad).

Torej sta sinus in kosinus definirana za vse kote rotacije, tangens je definiran za vse kote razen 90°+180°k, k∈Z (π/2+πk rad), kotangens pa je definiran za vse kote razen 180° ·k , k∈Z (π·k rad).

Definicije vključujejo že znane oznake sin, cos, tg in ctg, uporabljajo pa se tudi za označevanje sinusa, kosinusa, tangensa in kotangensa kota vrtenja (včasih lahko najdete oznake tan in cot, ki ustrezata tangensu in kotangensu) . Tako lahko sinus rotacijskega kota 30 stopinj zapišemo kot sin30°, vnosa tg(−24°17′) in ctgα ustrezata tangensu rotacijskega kota −24 stopinj 17 minut in kotangensu rotacijskega kota α . Spomnimo se, da pri pisanju radianske mere kota pogosto izpustimo oznako "rad". Na primer, kosinus rotacijskega kota treh pi rad je običajno označen s cos3·π.

Za zaključek te točke velja omeniti, da ko govorimo o sinusu, kosinusu, tangensu in kotangensu vrtilnega kota, pogosto izpustimo izraz "rotacijski kot" ali besedo "rotacija". To pomeni, da se namesto besedne zveze "sinus rotacijskega kota alfa" običajno uporablja besedna zveza "sinus kota alfa" ali še krajše, "sinus alfa". Enako velja za kosinus, tangens in kotangens.

Povedali bomo tudi, da so definicije sinusa, kosinusa, tangensa in kotangensa ostrega kota v pravokotnem trikotniku skladne z definicijami, ki so pravkar podane za sinus, kosinus, tangens in kotangens rotacijskega kota v razponu od 0 do 90 stopinj. To bomo utemeljili.

Številke

Opredelitev.

Sinus, kosinus, tangens in kotangens števila t je število, ki je enako sinusu, kosinusu, tangensu in kotangensu rotacijskega kota v t radianih.

Na primer, kosinus števila 8·π je po definiciji število, ki je enako kosinusu kota 8·π rad. In kosinus kota 8·π rad je enak ena, torej je kosinus števila 8·π enak 1.

Obstaja še en pristop k določanju sinusa, kosinusa, tangensa in kotangensa števila. Sestoji iz dejstva, da je vsako realno število t povezano s točko na enotskem krogu s središčem v izhodišču pravokotnega koordinatnega sistema, sinus, kosinus, tangens in kotangens pa so določeni preko koordinat te točke. Oglejmo si to podrobneje.

Pokažimo, kako se vzpostavi ujemanje med realnimi števili in točkami na krogu:

• številu 0 priredimo izhodišče A(1, 0);
• pozitivnemu številu t je pridružena točka na enotskem krogu, do katere pridemo, če se po krožnici premaknemo od začetne točke v nasprotni smeri urinega kazalca in prehodimo pot dolžine t;
• negativnemu številu t je pridružena točka na enotskem krogu, do katere pridemo, če se po krožnici premikamo od izhodišča v smeri urinega kazalca in prehodimo pot dolžine |t| .

Zdaj preidimo na definicije sinusa, kosinusa, tangensa in kotangensa števila t. Predpostavimo, da število t ustreza točki na krožnici A 1 (x, y) (na primer število &pi/2; ustreza točki A 1 (0, 1)).

Opredelitev.

Sinus števila t je ordinata točke na enotskem krogu, ki ustreza številu t, to je sint=y.

Opredelitev.

Kosinus števila t imenujemo abscisa točke enotskega kroga, ki ustreza številu t, to je cena=x.

Opredelitev.

Tangens števila t je razmerje med ordinato in absciso točke na enotskem krogu, ki ustreza številu t, to je tgt=y/x. V drugi enakovredni formulaciji je tangens števila t razmerje med sinusom tega števila in kosinusom, to je tgt=sint/strošek.

Opredelitev.

Kotangens števila t je razmerje med absciso in ordinato točke na enotskem krogu, ki ustreza številu t, to je ctgt=x/y. Druga formulacija je naslednja: tangens števila t je razmerje med kosinusom števila t in sinusom števila t: ctgt=cost/sint.

Tukaj ugotavljamo, da so pravkar navedene definicije skladne z definicijo, podano na začetku tega odstavka. Dejansko točka na enotskem krogu, ki ustreza številu t, sovpada s točko, ki jo dobimo z vrtenjem začetne točke za kot t radianov.

Še vedno je vredno pojasniti to točko. Recimo, da imamo vnos sin3. Kako lahko razumemo, ali govorimo o sinusu števila 3 ali sinusu rotacijskega kota 3 radianov? To je običajno jasno iz konteksta, sicer verjetno ni bistvenega pomena.

Trigonometrične funkcije kotnega in numeričnega argumenta

V skladu z definicijami, podanimi v prejšnjem odstavku, vsak rotacijski kot α ustreza zelo specifični vrednosti sinα, pa tudi vrednosti cosα. Poleg tega vsi rotacijski koti, razen 90°+180°k, k∈Z (π/2+πk rad), ustrezajo vrednostim tgα, vrednosti, ki niso 180°k, k∈Z (πk rad ) – vrednosti od ctgα. Zato so sinα, cosα, tanα in ctgα funkcije kota α. Z drugimi besedami, to so funkcije kotnega argumenta.

Podobno lahko govorimo o funkcijah sinus, kosinus, tangens in kotangens numeričnega argumenta. Dejansko vsako realno število t ustreza zelo specifični vrednosti sint, pa tudi strošku. Poleg tega vse številke razen π/2+π·k, k∈Z ustrezajo vrednostim tgt, številke π·k, k∈Z pa vrednostim ctgt.

Imenujemo funkcije sinus, kosinus, tangens in kotangens osnovne trigonometrične funkcije.

Običajno je iz konteksta jasno, ali imamo opravka s trigonometričnimi funkcijami kotnega argumenta ali numeričnega argumenta. V nasprotnem primeru si lahko neodvisno spremenljivko predstavljamo kot merilo kota (kotni argument) in numerični argument.

Vendar v šoli preučujemo predvsem numerične funkcije, torej funkcije, katerih argumenti in njihove ustrezne funkcijske vrednosti so števila. Če torej govorimo posebej o funkcijah, potem je priporočljivo trigonometrične funkcije obravnavati kot funkcije numeričnih argumentov.

Razmerje med definicijami iz geometrije in trigonometrije

Če upoštevamo vrtilni kot α v območju od 0 do 90 stopinj, potem so definicije sinusa, kosinusa, tangensa in kotangensa vrtilnega kota v kontekstu trigonometrije popolnoma skladne z definicijami sinusa, kosinusa, tangensa in kotangensa ostri kot v pravokotnem trikotniku, ki so podani pri tečaju geometrije. Utemeljimo to.

Upodabljajmo ga v pravokotniku kartezični sistem koordinate kroga enote Oxy. Opomba Izhodišče A(1, 0) . Zasukamo ga za kot α od 0 do 90 stopinj, dobimo točko A 1 (x, y). Spustimo navpičnico A 1 H iz točke A 1 na os Ox.

Zlahka je videti, da je v pravokotnem trikotniku kot A 1 OH enak rotacijskemu kotu α, dolžina kraka OH, ki meji na ta kot, je enaka abscisi točke A 1, to je | OH |=x, dolžina kraka A 1 H nasproti kotu je enaka ordinati točke A 1, to je |A 1 H|=y, dolžina hipotenuze OA 1 pa je enaka ena, saj je polmer enotskega kroga. Potem je po definiciji iz geometrije sinus ostrega kota α v pravokotnem trikotniku A 1 OH enak razmerju nasprotnega kraka proti hipotenuzi, to je sinα=|A 1 H|/|OA 1 |= y/1=y. In po definiciji iz trigonometrije je sinus rotacijskega kota α enak ordinati točke A 1, to je sinα=y. To kaže, da je določitev sinusa ostrega kota v pravokotnem trikotniku enakovredna določitvi sinusa rotacijskega kota α, ko je α od 0 do 90 stopinj.

Podobno je mogoče pokazati, da so definicije kosinusa, tangensa in kotangensa ostrega kota α skladne z definicijami kosinusa, tangensa in kotangensa rotacijskega kota α.

Bibliografija.

1. Geometrija. 7-9 razredi: učbenik za splošno izobraževanje ustanove / [L. S. Atanasjan, V. F. Butuzov, S. B. Kadomcev itd.]. - 20. izd. M .: Izobraževanje, 2010. - 384 str .: ilustr. - ISBN 978-5-09-023915-8.
2. Pogorelov A.V. Geometrija: Učbenik. za 7-9 razrede. Splošna izobrazba ustanove / A. V. Pogorelov. - 2. izd. - M .: Izobraževanje, 2001. - 224 str .: ilustr. - ISBN 5-09-010803-X.
3. Algebra in elementarne funkcije: Vadnica za učence 9. razreda Srednja šola/ E. S. Kočetkov, E. S. Kočetkova; Uredil doktor fizikalnih in matematičnih znanosti O. N. Golovin - 4. izd. M.: Izobraževanje, 1969.
4. Algebra: Učbenik za 9. razred. povpr. šola/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. Telyakovsky S. A. - M.: Izobraževanje, 1990. - 272 str.: ilustr. - ISBN 5-09-002727-7
5. Algebra in začetek analize: Proc. za 10-11 razrede. Splošna izobrazba institucije / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn in drugi; Ed. A. N. Kolmogorov - 14. izd. - M.: Izobraževanje, 2004. - 384 str .: ilustr. - ISBN 5-09-013651-3.
6. Mordkovič A. G. Algebra in začetki analize. 10. razred. Ob 2. str 1. del: vadnica za izobraževalne ustanove(raven profila)/ A. G. Mordkovich, P. V. Semenov. - 4. izd., dod. - M.: Mnemosyne, 2007. - 424 str .: ilustr. ISBN 978-5-346-00792-0.
7. Algebra in začel matematična analiza. 10. razred: učbenik. za splošno izobraževanje ustanove: osnovne in profilne. ravni / [Yu. M. Koljagin, M. V. Tkačeva, N. E. Fedorova, M. I. Šabunin]; uredil A. B. Žižčenko. - 3. izd. - I.: Vzgoja, 2010.- 368 str.: ilustr.- ISBN 978-5-09-022771-1.
8. Bašmakov M. I. Algebra in začetki analize: Učbenik. za 10-11 razrede. povpr. šola - 3. izd. - M .: Izobraževanje, 1993. - 351 str .: ilustr. - ISBN 5-09-004617-4.
9. Gusev V. A., Mordkovič A. G. Matematika (priročnik za vpisnike v tehnične šole): Proc. dodatek.- M.; višje šola, 1984.-351 str., ilustr.

Iz grafov je razvidno, da:

1. Sinusni in kosinusni grafi nihajo med -1 in 1
2. Kosinusna krivulja ima enako obliko kot sinusna krivulja, vendar je glede nanjo zamaknjena za 90 o
3. Sinusna in kosinusna krivulja sta zvezni in se ponavljata s periodo 360 o, tangentna krivulja ima prekinitve in se ponavlja s periodo 180 o.

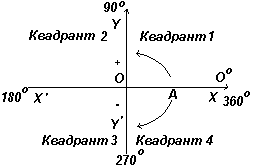Na sl. na levi sta pravokotni osi XX" in YY"; sekajo v izhodišču koordinat O. Pri delu z grafi se meritve v desno in navzgor od O štejejo za pozitivne, v levo in navzdol od O pa kot negativne. Naj se OA prosto vrti glede na O. Ko je OA zasukan v nasprotni smeri urinega kazalca, velja izmerjeni kot za pozitiven, pri zasuku v smeri urinega kazalca pa za negativnega.

Urnik. Pozitiven ali negativen
smer pri gibanju v krogu.

Naj se OA vrti v nasprotni smeri urinega kazalca tako, da je Θ 1 kateri koli kot v prvem kvadrantu, in zgradimo pravokotnik AB, da dobimo pravokotni trikotnik OAB na sliki. levo. Ker so vse tri stranice trikotnika pozitivne, bodo trigonometrične funkcije sinus, kosinus in tangens v prvem kvadrantu pozitivne. (Upoštevajte, da je dolžina OA vedno pozitivna, saj je polmer kroga.)
Naj se OA vrti naprej tako, da je Θ 2 poljuben kot v drugem kvadrantu, in konstruirajte AC tako, da nastane pravokotni trikotnik OAC. Potem je sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tan Θ 2 =+/- = -. Naj se OA vrti naprej tako, da je Θ 3 poljuben kot v tretjem kvadrantu, in konstruirajte AD tako, da nastane pravokotni trikotnik OAD. Potem je sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tan Θ 3 = -/- =+ .

Urnik. Konstruiranje kotov v
različne kvadrante.

Naj se OA vrti naprej tako, da je Θ 4 poljuben kot v četrtem kvadrantu, in konstruirajte AE tako, da nastane pravokotni trikotnik OAE. Potem je sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tan Θ 4 = -/+= -.

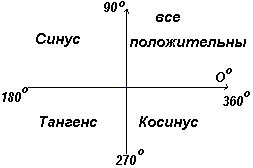
V prvem kvadrantu imajo vse trigonometrične funkcije pozitivne vrednosti, v drugem je pozitiven samo sinus, v tretjem samo tangens, v četrtem samo kosinus, kot je prikazano na sl. levo.

Poznavanje kotov poljubne velikosti je potrebno pri iskanju na primer vseh kotov med 0 o in 360 o, katerih sinus je recimo 0,3261. Če v kalkulator vnesete 0,3261 in pritisnete gumb sin -1, dobimo odgovor 19,03 o. Vendar pa obstaja drugi kot med 0 o in 360 o, ki ga kalkulator ne bo prikazal. Sinus je pozitiven tudi v drugem kvadrantu. Drugi kot je prikazan na sl. spodaj kot kot Θ, kjer je Θ=180 o - 19,03 o = 160,97 o. Tako sta 19,03 o in 160,97 o kota v območju od 0 o do 360 o, katerih sinus je 0,3261.

Bodi previden! Kalkulator poda samo eno od teh vrednosti. Drugo vrednost je treba določiti po teoriji poljubnih kotov.

Primer 1

Poiščite vse kote v območju od 0 o do 360 o, katerih sinus je -0,7071

rešitev:
Kota, katerih sinus je -0,7071 o, sta v tretjem in četrtem kvadrantu, saj je sinus v teh kvadrantih negativen (glej sliko na levi).

Urnik. Iskanje vseh kotov z
dana sinusna vrednost (primer)

Iz naslednje slike je Θ = arcsin 0,7071 = 45 o. Dva kota v območju od 0 o do 360 o, katerih sinus je -0,7071, sta 180 o +45 o = 225 o in 360 o - 45 o = 315 o.

Opomba. Kalkulator daje samo en odgovor.
Urnik. Iskanje vseh kotov z
dana sinusna vrednost (primer)

Primer 2

Poiščite vse kote med 0 o in 360 o, katerih tangens je 1,327.

rešitev:
Tangenta je pozitivna v prvem in tretjem kvadrantu - sl. levo.
Urnik. Iskanje vseh kotov z

Iz spodnje slike je Θ = arctan1,327= 53 o.
Dva kota v območju od 0 o do 360 o, katerih tangens je 1,327, sta 53 o in 180 o + 53 o, tj. 233 o.
Urnik. Iskanje vseh kotov z
dana tangentna vrednost (primer)

Naj bo ALI na sl. na levi je vektor enotske dolžine, ki se prosto vrti v nasprotni smeri urinega kazalca okoli O. En obrat ustvari krog, prikazan na sl. in razdeljen na sektorje po 15 o. Vsak radij ima vodoravno in navpično komponento. Na primer, za 30 o je navpična komponenta TS, vodoravna komponenta pa OS.

Iz definicije trigonometričnih funkcij
sin30 o =TS/TO=TS/1, tj. TS= sin30 o in cos30 o =OS/TO=OS/1, tj. OS=cos30 o

Navpično komponento TS lahko narišemo kot T"S", ki je enaka vrednosti, ki ustreza kotu 30 o na grafu odvisnosti y od kota x. Če vse navpične komponente, kot je TS, prenesemo na graf, bomo dobili sinusoid, prikazan na sl. višji.

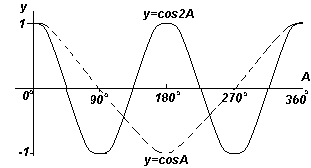
Če vse vodoravne komponente, kot je OS, projiciramo na graf y glede na kot x, je rezultat kosinusni val. Te projekcije je mogoče preprosto prikazati tako, da narišete krog s polmerom ALI in koti, ki izvirajo iz navpičnice, kot je prikazano na sliki na levi.
Iz sl. na levi lahko vidite, da ima sinusni val enako obliko kot kosinusni val, vendar premaknjen za 90 o.

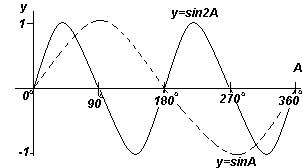Periodične funkcije in perioda
Vsak od funkcijskih grafov, prikazanih na štirih sl. zgoraj, se ponavlja, ko se kot A povečuje, zato se imenujejo periodične funkcije.
Funkciji y=sinA in y=cosA se ponovita vsakih 360 o (ali 2π radiana), zato se 360 ​​o imenuje obdobje te funkcije. Funkciji y=sin2A in y=cos2A se ponovita vsakih 180 o (ali π radianov), tako da je 180 o perioda za ti funkciji.
Na splošno, če je y=sinpA in y=cospA (kjer je p konstanta), potem je perioda funkcije 360 ​​o /p (ali 2π/p radianov). Če je torej y=sin3A, potem je perioda te funkcije enaka 360 o /3= 120 o, če je y=cos4A, potem je perioda te funkcije enaka 360 o /4= 90 o.

Amplituda
Amplituda se imenuje največja vrednost sinusoide. Vsak od grafov 1-4 ima amplitudo +1 (tj. nihajo med +1 in -1). Če pa je y=4sinA, se vsaka od vrednosti sinA pomnoži s 4, tako da je največja vrednost amplitude 4. Podobno je za y=5cos2A amplituda 5 in perioda 360 o /2 = 180 o .

Primer 3.
Konstruirajte y=3sin2A v območju od A=0 o do A=360 o.

rešitev:
Amplituda =3, perioda = 360 o /2 =180 o.

Primer 4.
Narišite graf za y=4cos2x v območju od x=0 o do x=360 o

rešitev:
Amplituda = 4. Perioda = 360 o /2 =180 o.

Koti zaostajanja in napredovanja
Sinusne in kosinusne krivulje se ne začnejo vedno pri 0 o. Da bi upoštevali to dejstvo, periodična funkcija je predstavljen kot y=sin(A± α), kjer je α fazni zamik glede na y=sinA in y=cosA.

Ko sestavite tabelo vrednosti, lahko zgradite graf funkcije y=sin(A-60 o), prikazano na sl. levo. Če se krivulja y=sinA začne pri 0 o, potem se krivulja y=sin(A-60 o) začne pri 60 o (tj. njena ničelna vrednost je 60 o v desno). Tako pravijo, da je y=sin(A-60 o) pozno je glede na y=sinA za 60 o.
Urnik. y=sin(A-60 o) (sinusoida).

S sestavljanjem tabele vrednosti lahko zgradite graf funkcije y=cos(A+45 o), prikazano na sl. spodaj.
Če se krivulja y=cosA začne pri 0 o, potem se krivulja y=cos(A+45 o) začne 45 o v levo (tj. njena ničelna vrednost je 45 o prej).
Tako naj bi bil graf y=cos(A+45 o) naprej graf y=cosA pri 45 o.
Urnik. y=cos(A+45 o) (kosinusni val).

Na splošno graf y=sin(A-α) zaostaja glede na y=sinA za kot α.
Kosinusni val ima enako obliko kot sinusni val, vendar se začne 90 o v levo, tj. pred njo za 90 o. Zato je cosA=sin(A+90 o).

Primer 5.
Nariši graf y=5sin(A+30 o) v območju od A=0 o do A=360 o

rešitev:
Amplituda = 5, perioda = 360 o /1 = 360 o.
5sin(A+30 o) je pred 5sinA za 30 o, tj. se začne 30 ur prej.
Graf y=5sin(A+30 o) (sinusoida).

Primer 6.
Nariši graf y=7sin(2A-π/3) v območju od A=0 o do A=360 o.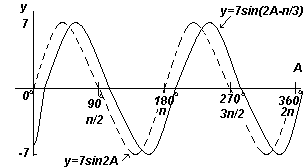

rešitev:
Amplituda = 7, perioda =2π/2= π radianov
Na splošno y=sin(pt-α) zaostaja glede na y=sinpt za α/p, zato 7sin(2A-π/3) zaostaja za 7sin2A za (π/3)/2, tj. za π/6 radianov ali 30 o

Sinusoida oblike Asin(ωt±α). Fazni kot. Fazni premik.

Naj bo ALI na sl. na levi je vektor, ki se prosto vrti v nasprotni smeri urinega kazalca okoli O s hitrostjo ω radianov/s. Rotacijski vektor se imenuje fazni vektor. Po času t sekund se bo OR zavrtel za kot ωt radianov (na sliki na levi je to kot TOR). Če konstruiramo ST pravokotno na OR, potem je sinωt=ST/OT, tj. ST=OTsinωt.
Če vse take navpične komponente projiciramo na graf y glede na ωt, dobimo sinusoid z amplitudo OR.

Če fazni vektor OR naredi en obrat (tj. 2π radianov) v T sekundah, potem je kotna hitrost ω=2π/T rad/s, od koder
T=2π/ ω (s), kjer je
T je obdobje
Imenuje se število popolnih obdobij, ki pretečejo v 1 sekundi pogostost f.
Frekvenca = (število obdobij)/(sekunda) = 1/ T = ω/2π Hz, tiste. f = ω/2π Hz
Zato je kotna hitrost
ω=2πf rad/s.

Če na splošno sinusna funkcija izgleda kot y=sin(ωt± α), potem
A - amplituda
ω - kotna hitrost
2π/ ω - obdobje T, s
ω/2π - frekvenca f, Hz
α je kot napredovanja ali zaostanka (glede na y=Аsinωt) v radianih, imenujemo ga tudi fazni kot.

Primer 7.
Izmenični tok je podan kot i=20sin(90πt+0,26) amperov. Določite amplitudo, periodo, frekvenco in fazni kot (v stopinjah)

rešitev:
i=20sin(90πt+0,26)In zato
amplituda je 20 A
kotna hitrost ω=90π, torej
obdobje T= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
pogostost f= 1/T = 1/0,022 = 45,46 Hz
fazni kot α= 0,26 rad. = (0,26*180/π) o = 14,9 o.

Primer 8.
Nihajni mehanizem ima največji premik 3 m in frekvenco 55 Hz. V času t=0 je premik 100 cm. Izrazite premik v splošni obliki Аsin(ωt± α).

rešitev
Amplituda = največji premik = 3 m
Kotna hitrost ω=2πf = 2π(55) = 110 πrad/s
Zato je premik 3sin(110πt + α) m.
Pri t=0 pomik = 100cm=1m.
Zato je 1= 3sin(0 + α), tj. sinα=1/3=0,33
Zato je α=arcsin0,33=19 o
Torej je odmik 3sin(110 πt + 0,33).

Primer 9.
Vrednost trenutne napetosti v tokokrogu izmeničnega toka v kateri koli t sekundi je podana kot v=350sin(40πt-0,542)V. Najti:
a) Amplituda, perioda, frekvenca in fazni kot (v stopinjah)
b) vrednost napetosti pri t =0
c) vrednost napetosti pri t = 10 ms
d) čas, v katerem napetost prvič doseže 200 V.
rešitev:
a) Amplituda je 350 V, kotna hitrost je ω=40π
torej
obdobje T=2π/ ω=2π/40π=0,05 s =50ms
frekvenca f=1/T=1/0,05=20 Hz
fazni kot = 0,542 rad (0,542*180/π) = 31 o z zamikom glede na v=350sin(40πt)
b) Če je t =0, potem je v=350sin(0-0,542)=350sin(-31 o)=-180,25 V
c) Če je t =10 ms, potem je v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6 V
d) Če je v=200 I, potem je 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

Urnik. Oscilacijski mehanizem
(primer, sinusni val).

v=350sin(40πt-0,542) Zato je (40πt-0,542)=arcsin200/350=35 o ali 0,611 rad.
40πt= 0,611+0,542=1,153.
Torej, če je v=200V, potem je čas t=1,153/40π=9,179 ms

Geometrijska definicija sinusa in kosinusa

\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)

α - kot, izražen v radianih.

Sinus (sin α) je trigonometrična funkcija kota α med hipotenuzo in krakom pravokotnega trikotnika, enaka razmerju dolžine nasprotnega kraka |BC| na dolžino hipotenuze |AB|.

Kosinus (cos α) je trigonometrična funkcija kota α med hipotenuzo in krakom pravokotnega trikotnika, enaka razmerju dolžine sosednjega kraka |AC| na dolžino hipotenuze |AB|.

Trigonometrična definicija

Z zgornjimi formulami lahko najdete sinus in kosinus ostrega kota. Vendar se morate naučiti izračunati sinus in kosinus poljubno velikega kota. Pravokotni trikotnik ne ponuja takšne priložnosti (na primer ne more imeti tupega kota); zato je potrebno več splošna definicija sinus in kosinus, ki vsebuje navedene formule kot poseben primer.

Na pomoč priskoči trigonometrični krog. Naj bo podan nek kot; ustreza istoimenski točki na trigonometričnem krogu.

riž. 2. Trigonometrična definicija sinusa in kosinusa

Kosinus kota je abscisa točke. Sinus kota je ordinata točke.

Na sl. 2 je kot oster in to je lahko razumeti ta definicija sovpada s splošnim geometrijska definicija. Pravzaprav vidimo pravokotni trikotnik z enoto hipotenuzo O in ostrim kotom. Sosednji krak tega trikotnika je cos (primerjaj s sliko 1) in hkrati abscisa točke; nasprotna stranica je sin (kot na sliki 1) in hkrati ordinata točke.

Zdaj pa nismo več omejeni s prvo četrtino in imamo možnost, da to definicijo razširimo na kateri koli kot. Na sl. Slika 3 prikazuje, koliko sta sinus in kosinus kota v drugi, tretji in četrti četrtini.

riž. 3. Sinus in kosinus v II, III in IV četrtini

Tabela vrednosti sinusa in kosinusa

Ničelni kot \(\LARGE 0^(\circ ) \)

Abscisa točke 0 je enaka 1, ordinata točke 0 je enaka 0. torej

cos 0 = 1 sin 0 = 0

Slika 4. Ničelni kot

Kot \(\LARGE \frac(\pi)(6) = 30^(\circ )\)

Vidimo pravokotni trikotnik z enoto hipotenuzo in ostrim kotom 30°. Kot veste, je krak, ki leži nasproti kota 30°, enak polovici hipotenuze 1; z drugimi besedami, navpični krak je enak 1/2 in zato

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Vodoravni krak najdemo s pomočjo Pitagorovega izreka (ali, kar je isto, kosinus najdemo z uporabo osnovne trigonometrične identitete):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \desno)^(2) ) =\frac(\sqrt(3) )(2 ) \]

1 Zakaj se to zgodi? Izrežite enakostranični trikotnik s stranico 2 po njegovi višini! Razcepi se na dva pravokotna trikotnika s hipotenuzo 2, ostrim kotom 30° in krajšim krakom 1.

Slika 5. Kot π/6

Kot \(\LARGE \frac(\pi)(4) = 45^(\circ )\)

V tem primeru je pravokotni trikotnik enakokrak; Sinus in kosinus kota 45° sta med seboj enaka. Označimo jih za zdaj z x. Imamo:

\[ x^(2) + x^(2) = 1 \]

od koder \(x=\frac(\sqrt(2) )(2) \). torej

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Slika 5. Kot π/4

Lastnosti sinusa in kosinusa

Sprejete notacije

\(\sin^2 x \ekviv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \ekviv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \ekviv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Periodičnost

Funkciji y = sin x in y = cos x sta periodični s periodo 2π.

\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)

Pariteta

Sinusna funkcija je liha. Kosinusna funkcija je soda.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Področja definicije in vrednosti, ekstremi, naraščanje, padanje

Osnovne lastnosti sinusa in kosinusa so predstavljene v tabeli ( n- celota).

	\(\majhen< x < \)	\(\majhen -\pi + 2\pi n \) \(\majhen< x < \) \(\small 2\pi n \)
Sestopanje	\(\majhen \dfrac(\pi)2 + 2\pi n \)\(\majhen< x < \) \(\majhen \dfrac(3\pi)2 + 2\pi n \)	\(\majhna 2\pi n \) \(\majhna< x < \) \(\pi + \small 2\pi n \)
Največ, \(\majhni x = \) \(\majhen \dfrac(\pi)2 + 2\pi n \)	\(\majhen x = 2\pi n\)
Minimum, \(\majhen x = \) \(\majhno -\dfrac(\pi)2 + 2\pi n \)	\(\majhen x = \) \(\majhen \pi + 2\pi n \)
Ničle, \(\mali x = \pi n\)	\(\mali x = \dfrac(\pi)2 + \pi n \)
Presečišča osi Y, x = 0	y = 0	y = 1

Osnovne formule, ki vsebujejo sinus in kosinus

Vsota kvadratov

\(\sin^2 x + \cos^2 x = 1\)

Sinusne in kosinusne formule za vsoto in razliko

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\levo(\dfrac(\pi)2 - x \desno) = \sin x \) ; \(\sin\levo(\dfrac(\pi)2 - x \desno) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Formule za produkt sinusov in kosinusov

\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)

Formule vsote in razlike

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Izražanje sinusa skozi kosinus

\(\sin x = \cos\levo(\dfrac(\pi)2 - x \desno) = \)\(\cos\levo(x - \dfrac(\pi)2 \desno) = - \cos\levo(x + \dfrac(\pi)2 \desno) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Izražanje kosinusa skozi sinus

\(\cos x = \sin\levo(\dfrac(\pi)2 - x \desno) = \)\(- \sin\levo(x - \dfrac(\pi)2 \desno) = \sin\levo(x + \dfrac(\pi)2 \desno) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Izražanje skozi tangento

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

pri \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

pri \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Tabela sinusov in kosinusov, tangensov in kotangensov

Ta tabela prikazuje vrednosti sinusov in kosinusov za določene vrednosti argumenta.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="Tabela sinusov in kosinusov" title="Tabela sinusov in kosinusov" ]!}

Izrazi skozi kompleksne spremenljivke

\(i^2 = -1\)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Eulerjeva formula

\(e^(iz) = \cos z + i \sin z \)

Izrazi s hiperboličnimi funkcijami

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Odvod

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Izpeljava formul >>>

Izpeljanke n-tega reda:
\(\levo(\sin x \desno)^((n)) = \sin\levo(x + n\dfrac(\pi)2 \desno) \)\(\levo(\cos x \desno)^((n)) = \cos\levo(x + n\dfrac(\pi)2 \desno) \).

Integrali

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Glej tudi poglavje Tabela nedoločenih integralov >>>

Razširitve serije

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Sekans, kosekans

\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)

Inverzne funkcije

Inverzni funkciji sinusa in kosinusa sta arkusin in arkosinus.

Arksin, arcsin

\(y = \arcsin x\) \(\levo\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \desno\) \)
\(\sin(\arcsin x) = x\)
\(\arcsin(\sin x) = x\) \(\levo\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \desno\) \)

Arkosinus, arkos

\(y = \arccos x\) \(\levo\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \desno\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x\) \(\( 0 \leqslant x \leqslant \pi \) \)

Reference:
I.N. Bronstein, K.A. Semendjajev, Priročnik matematike za inženirje in študente, “Lan”, 2009.

Javascript je onemogočen v vašem brskalniku.
Za izvajanje izračunov morate omogočiti kontrolnike ActiveX!

Središče v točki A.
α je kot, izražen v radianih.

Tangenta ( tan α) je trigonometrična funkcija, odvisna od kota α med hipotenuzo in krakom pravokotnega trikotnika, ki je enak razmerju dolžine nasprotnega kraka |BC| na dolžino sosednjega kraka |AB| .

Kotangens ( ctg α) je trigonometrična funkcija, odvisna od kota α med hipotenuzo in krakom pravokotnega trikotnika, enaka razmerju dolžine sosednjega kraka |AB| na dolžino nasprotnega kraka |BC| .

Tangenta

Kje n- cela.

V zahodni literaturi je tangenta označena na naslednji način:
.
;
;
.

Graf funkcije tangente, y = tan x

Kotangens

Kje n- cela.

V zahodni literaturi je kotangens označen na naslednji način:
.
Sprejemljivi so tudi naslednji zapisi:
;
;
.

Graf funkcije kotangens, y = ctg x

Lastnosti tangensa in kotangensa

Periodičnost

Funkcije y = tg x in y = ctg x so periodični s periodo π.

Pariteta

Funkciji tangens in kotangens sta lihi.

Področja opredelitve in vrednosti, naraščanje, padanje

Funkciji tangens in kotangens sta zvezni v svoji definicijski domeni (glej dokaz kontinuitete). Glavne lastnosti tangensa in kotangensa so predstavljene v tabeli ( n- celota).

	y= tg x	y= ctg x
Obseg in kontinuiteta
Razpon vrednosti	-∞ < y < +∞	-∞ < y < +∞
Povečanje		-
Sestopanje	-
Ekstremi	-	-
Ničle, y = 0
Presečišča z ordinatno osjo, x = 0	y= 0	-

Formule

Izrazi z uporabo sinusa in kosinusa

; ;
; ;
;

Formule za tangens in kotangens iz vsote in razlike

Preostale formule je na primer enostavno dobiti

Produkt tangent

Formula za vsoto in razliko tangent

Ta tabela predstavlja vrednosti tangentov in kotangensov za določene vrednosti argumenta.

Izrazi, ki uporabljajo kompleksna števila

Izrazi s hiperboličnimi funkcijami

;
;

Odvod

; .

.
Odvod n-tega reda glede na spremenljivko x funkcije:
.
Izpeljava formul za tangento >>> ; za kotangens >>>

Integrali

Razširitve serije

Če želite dobiti raztezanje tangente po potencah x, morate vzeti več členov raztezanja v potenčni vrsti za funkcije greh x in cos x in te polinome razdelite drug z drugim, . To ustvari naslednje formule.

Ob .

ob .
Kje Bn- Bernoullijeva števila. Določeni so bodisi iz povratne relacije:
;
;
Kje .
Ali po Laplaceovi formuli:

Inverzne funkcije

Inverzni funkciji tangensa in kotangensa sta arktangens in arkotangens.

Arktangens, arctg

, Kje n- cela.

Arkotangens, arcctg

, Kje n- cela.

Reference:
I.N. Bronstein, K.A. Semendjajev, Priročnik matematike za inženirje in študente, “Lan”, 2009.
G. Korn, Priročnik iz matematike za znanstvenike in inženirje, 2012.

Osredotočeno na točko A.
α - kot, izražen v radianih.

Opredelitev
Sinus (sin α) je trigonometrična funkcija, odvisna od kota α med hipotenuzo in krakom pravokotnega trikotnika, ki je enak razmerju dolžine nasprotnega kraka |BC| na dolžino hipotenuze |AC|.

Kosinus (cos α) je trigonometrična funkcija, odvisna od kota α med hipotenuzo in krakom pravokotnega trikotnika, enaka razmerju dolžine sosednjega kraka |AB| na dolžino hipotenuze |AC|.

Sprejete notacije

;
;
.

;
;
.

Graf sinusne funkcije, y = sin x

Graf kosinusne funkcije, y = cos x

Lastnosti sinusa in kosinusa

Periodičnost

Funkcije y = greh x in y = cos x periodično z obdobjem 2π.

Pariteta

Sinusna funkcija je liha. Kosinusna funkcija je soda.

Področje definicije in vrednosti, ekstremi, naraščanje, padanje

Funkciji sinus in kosinus sta zvezni v svoji definicijski domeni, to je za vse x (glejte dokaz zveznosti). Njihove glavne lastnosti so predstavljene v tabeli (n - celo število).

	y= greh x	y= cos x
Obseg in kontinuiteta	- ∞ < x < + ∞	- ∞ < x < + ∞
Razpon vrednosti	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Povečanje
Sestopanje
Maksimalno, y = 1
Najmanjše vrednosti, y = - 1
Ničle, y = 0
Presečišča z ordinatno osjo, x = 0	y= 0	y= 1

Osnovne formule

Vsota kvadratov sinusa in kosinusa

Formule za sinus in kosinus iz vsote in razlike

;
;

Formule za produkt sinusov in kosinusov

Formule vsote in razlike

Izražanje sinusa skozi kosinus

;
;
;
.

Izražanje kosinusa skozi sinus

;
;
;
.

Izražanje skozi tangento

; .

Ko imamo:
; .

ob:
; .

Tabela sinusov in kosinusov, tangensov in kotangensov

Ta tabela prikazuje vrednosti sinusov in kosinusov za določene vrednosti argumenta.

Izrazi skozi kompleksne spremenljivke

;

Eulerjeva formula

Izrazi s hiperboličnimi funkcijami

;
;

Odvod

; . Izpeljava formul >>>

Izpeljanke n-tega reda:
{ -∞ < x < +∞ }

Sekans, kosekans

Inverzne funkcije

Inverzni funkciji sinusa in kosinusa sta arkusin in arkosinus.

Arksin, arcsin

Arkosinus, arkos

Reference:
I.N. Bronstein, K.A. Semendjajev, Priročnik matematike za inženirje in študente, “Lan”, 2009.